【摘要】:在ANSYS有限元数值模拟损伤识别过程,通过设置脱空参数包围范围内的表面单元EFS=0来模拟实际水闸底板地基的脱空状态。由图7.3.2可以看出,响应面精度均在千分之几内,响应面精度结果较好,认为可以满足后续遗传算法反演识别的要求。
以顺水流贯穿脱空为例进行建模说明,多侧等其他类型脱空所用的理论方法与此相同。由前文可知,目标函数中仅含有结构频率导致识别结果不太理想,本节的多侧脱空识别控制参数个数增加至10个,理论上识别难度将会增加,故本节将采用水闸结构前6阶频率和8个测点的振型值数据来建立响应面,进行多侧脱空情况下的脱空控制参数的反演。响应面公式:
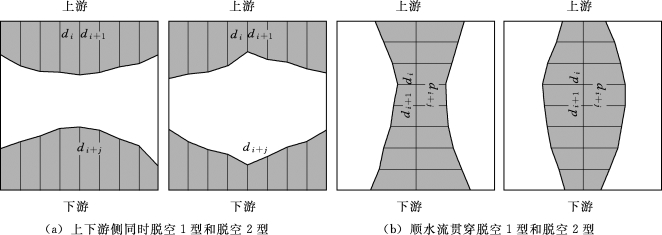
图7.3.1 底板多侧脱空形式

式中:y为模态信息,本节中为水闸结构前6阶频率和8个测点的振型值数据;xi为第i个脱空控制参数的脱空区域值,本节中i=10,即设10个脱空控制参数,每侧5个,β为待定系数。(https://www.xing528.com)
通过对比分析,当n=10时能在合理的时间内有效计算,保证结果的可靠性,且足够描述脱空区域;考虑到水闸底板尺寸,本章中脱空参数di范围取0~4m。在ANSYS有限元数值模拟损伤识别过程,通过设置脱空参数包围范围内的表面单元EFS=0来模拟实际水闸底板地基的脱空状态。根据公式计算出精度值,列举出几个响应面精度,如图7.3.2所示。

式中:yRS为响应面模型的输出值;y为ANSYS有限元计算的结构参数值。
由图7.3.2可以看出,响应面精度均在千分之几内,响应面精度结果较好,认为可以满足后续遗传算法反演识别的要求。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




