基于频率信息的脱空识别方法优化

7.2.1.1　响应面模型的建立

以偏左侧脱空进行说明，其他单侧脱空类型所运用的理论方法相似。首先，需确定合适的响应面公式，通过研究分析和试算选取3阶不带交叉项的响应面公式，形式如下：

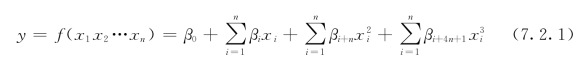
式中：y为模态信息；xi为第i个脱空控制参数的脱空区域值，本节中i=5，即设5个脱空控制参数；β为待定系数。

其次，为了更合理构造响应面模型，用MATLAB编写拉丁抽样程序。

利用抽样程序随机抽取500组偏左侧脱空数据作为脱空控制参数di（i=1，2，…，n），通过对比分析，当n=5时，能在合理的时间内有效计算并保证结果的可靠性。考虑到水闸底板尺寸，防止脱空过大而导致水闸结构整体倾覆，脱空控制参数取值不宜超过底板尺寸的一半，本章中脱空控制参数di取值范围为0～6m。

在ANSYS有限元数值模拟损伤识别过程，通过设置脱空控制参数包围范围内的表面单元EFS=0来模拟实际水闸底板地基的脱空状态。结合水闸实体模型，提取出偏左侧脱空情况下相应的前三阶频率，拟合出响应面模型替代有限元模型，并对比水闸结构固有频率和响应面计算的频率之间的误差。

响应面代理模型的精度计算公式如下：

式中：yRS为响应面模型的输出值；y为有限元模型的输出值。

图7.2.2为水闸结构第1阶固有频率的响应面精度，在5×10-4之内；图7.2.3为水闸结构第2阶固有频率的响应面精度，在2×10-5之内；图7.2.4为水闸结构第三阶固有频率的响应面精度，在8×10-3之内。可见这些精度都能满足要求。

图7.2.2　水闸结构第1阶固有频率的响应面精度

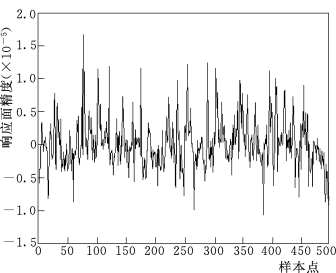
图7.2.3　水闸结构第2阶固有频率的响应面精度

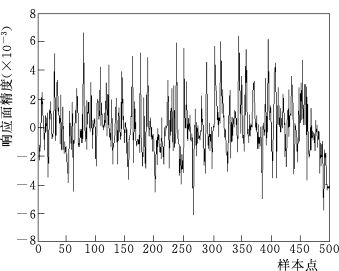
图7.2.4　水闸结构第3阶固有频率的响应面精度

7.2.1.2　基于遗传算法的脱空区域识别结果

不同的模态数据可以构造不同的目标函数，本章先由结构频率来构造遗传算法中的目标函数。

定义结构固有频率向量为

式中：n为阶数，此处n=3。

根据模拟的脱空情况，利用响应面模型求得的结构频率向量定义如下：(www.xing528.com)

式中：n为阶数，此处n=3。

定义优化问题的目标函数为

式中：k为响应面数据点个数，k=3。

遗传算法是一种全局性的优化方法，其核心思想是优胜劣汰。理论和实践都证明遗传算法能很好地解决非线性的优化问题，但在结构损伤识别问题的运用上则存在运算量过大的问题。采用上文建立的响应面模型取代有限元模型，借助改进后的遗传算法能解决这一困难从而进行快速的优化求解，极大地提高了计算效率，节约时间，保证精度。

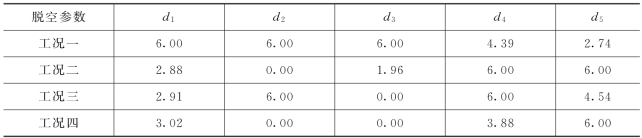
为尽可能涵盖到实际可能发生的工况，对计算工况进行构造如下：偏左侧脱空，偏右侧脱空，中间脱空，左右侧同时脱空，分别命名为工况一、工况二、工况三和工况四。水闸底板脱空参数设置见表7.2.1。

四种脱空工况脱空参数识别结果见表7.2.2和图7.2.5。

表7.2.1　水闸底板脱空参数设置　单位：m

表7.2.2　脱空参数识别结果（无噪声）　单位：m

图7.2.5　无噪声情况下四种脱空工况的脱空参数识别结果

从以上四种工况的脱空识别结果可以看出，在不考虑实际操作过程中的环境误差、测量误差和结构模型误差等，即在无噪声的情况下，仅使用前3阶结构频率构建目标函数基本能识别出水闸底板的大致脱空区域。

在实际水闸底板脱空检测识别中，由于水闸在工作情况下水流环境会导致测量过程中有噪声，并且仪器精度和人为测量过程中会有不可避免的误差存在，所以为了更贴合实际，本文将进行有噪声情况下的水闸底板脱空识别。分别施加噪声级别1%的高斯白噪声来效仿实际操作中不可避免的误差。

式中：d为施加噪声前的模态值；dM为施加噪声后的模态值，此处为结构固有频率；γ为噪声水平；Ri为在[-1，1]之间的随机分布变量，利用公式进行误差的模拟，即加入噪声，根据施加噪声后的模态数据进行脱空控制参数的反演，从而能识别水闸底板的脱空区域。

四种脱空工况施加1%噪声后的参数识别结果见表7.2.3和图7.2.6。

表7.2.3　四种脱空工况施加1%噪声后的参数识别结果　单位：m

从加1%噪声后的脱空识别结果来看，仅仅以前3阶结构的频率构建的目标函数识别结果比较差，分析可能的原因有以下两点：第一，从表7.1.2可以看出部分脱空的情况下前3阶固有频率的变化率非常小，第1阶和第2阶的变化率均在1%以下，第3阶也只有7%左右，所以变化率本身就不大，这是导致抗噪能力在1%以下的主要原因；第二，仅以前3阶频率构建的目标函数，其信息量太小，导致脱空控制参数反演的不适定性较突出，从而导致不抗噪，故为解决这一个问题，在下一节将增大其信息量。