软基水闸结构模态分析

基于ANSYS有限元软件用模态分析方法可以得出该模型在无脱空情况下的结构频率。为验证水闸底板脱空会对结构频率产生一定的影响，对该模型在部分脱空情况下的结构频率进行分析。水闸底板单侧脱空参数见表7.1.1，对水闸底板无脱空和部分脱空工况进行对比分析，分析结果见表7.1.2。

表7.1.1　水闸底板单侧脱空参数　单位：m

表7.1.2　软基部分脱空情况对水闸结构固有频率的影响

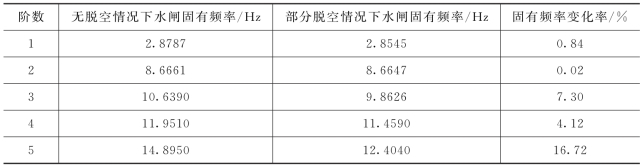
由表7.1.2可知，部分脱空情况下水闸的固有频率比无脱空情况下水闸的固有频率小，随着阶数的增加，部分脱空情况下的固有频率减小幅度有变大的趋势，尤其是到第5阶，固有频率变化率高达16.72%，第1阶和第2阶变化率较小，在1%以内，第3阶和第4阶在1%～10%之间；所以，闸底板脱空会使结构的固有频率发生变化，且阶数增大，变化明显。

如图7.1.2所示，水闸结构模型的前5阶位移矢量和振型图的规律为：第1阶，结构整体从下至上位移矢量和逐渐增大，两侧的闸墩向相同方向同步摆动；第2阶，水闸整体沿水流方向的位移矢量和呈增大趋势，且在竖直方向上水闸位移矢量和从下至上增大，两侧的闸墩方向相反、同步摆动，且靠上部分摆动最明显；第3阶，水闸整体从下至上位移矢量和呈逐渐增大趋势，水闸整体下部结构基本无位移，上部结构位移矢量和较大，和前几阶不同的是第3阶变形为整体扭动，两侧闸墩为同步、同向扭动，中间部分工作桥处无明显变化；第4阶，水闸的工作桥连接段呈波浪形运动，且工作桥中间靠近上游位置最明显，水闸其他部位基本无位移变化；第5阶和第4阶类似，但整体位移矢量和较第4阶大，水闸的工作桥连接段呈波浪形运动，但不同的是工作桥中间靠近下游位置最明显。(www.xing528.com)

图7.1.2　水闸结构模型的前5阶位移矢量和振型图

对结构在有无脱空情况下的横向（X方向）、纵向（Y方向）和竖向（Z方向）第1阶和第2阶振型数据进行变化率分析，发现结构振型数据在竖向（Z方向）的变化率较大，部分脱空情况对结构的竖向（Z方向）振型影响较大。表7.1.3给出了水闸结构模型无脱空情况下的第1阶和第2阶竖向（Z方向）振型，同时列出了水闸结构模型部分脱空情况下的第1阶和第2阶竖向（Z方向）振型，并进行对比。

表7.1.3　软基部分脱空情况对水闸结构振型的影响

通过列举的前两阶无脱空情况和部分脱空情况下水闸结构竖向（Z方向）振型数据，发现部分脱空后的水闸竖向（Z方向）振型与无脱空情况下的水闸竖向（Z方向）振型有明显差别，特别是结构中部测点（4号、5号）以及脱空附近测点（1号、6号），有的变化率达100%以上，该数据和结论有利于后期脱空识别。所以，结构的频率和振型值可以用来分析水闸底板的脱空情况。

水闸模型底板发生脱空后，其振型会发生变化，且与脱空的形式有关，脱空较严重的一侧振动幅度变大。故可以先通过分析振型数据，为脱空区域识别工作提供一定的先验信息，确定可能的脱空类型，分别选用相应的响应面模型进行拟合，借助遗传算法构造目标函数，对比每种脱空类型的目标残差，最小的残差对应的脱空类型识别结果则为最优。