弹性地基刚度的模拟方法优化策略

在模拟闸基脱空时，需在水闸模型底板底层附加Surf154单元，通过在实常数中设置EFS（即弹性地基刚度）来模拟温克尔地基。本节通过简单模型验证，分析对比弹性地基刚度EFS模拟温克尔地基（图6.3.1）与弹簧元模拟温克尔地基（图6.3.2）对结构模态的影响。基于ANSYS建立实体底板，其下地基分别采用弹性地基刚度EFS和弹簧元模拟，分析两种情况下结构模态的区别。

图6.3.1　EFS模拟温克尔地基图

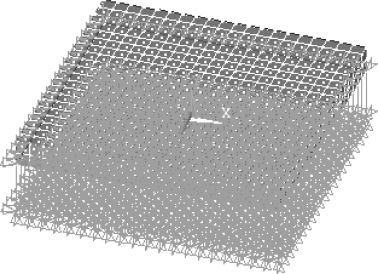
图6.3.2　弹簧元模拟温克尔地基图

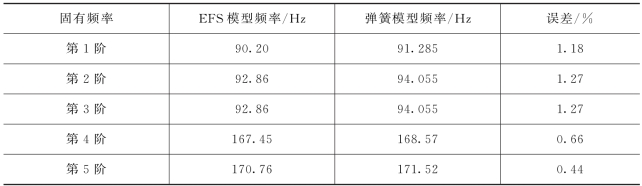
两个模型的材料参数、结构尺寸、约束条件完全一致。弹簧刚度：中=EFS×单元面积×1/4×4；边=EFS×单元面积×1/4×2；角=EFS×单元面积×1/4×1。两种情况计算的模态对比如表6.3.1和图6.3.3～图6.3.5所示。

表6.3.1　无脱空情况下水闸结构固有频率

(www.xing528.com)

图6.3.3　第1阶模态振型图对比

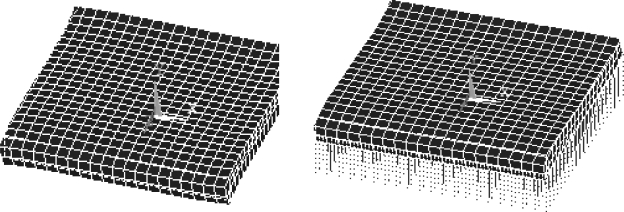
图6.3.4　第2阶模态振型图对比

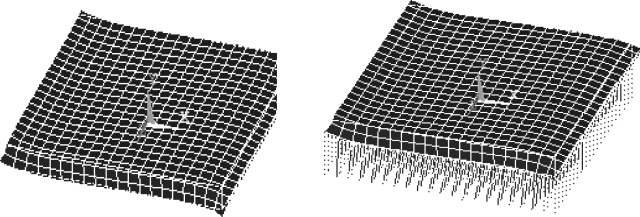
图6.3.5　第3阶模态振型图对比

由以上固有频率对比结果来看，两种情况下固有频率变化规律一致，且平均误差小于1%，故从固有频率角度看，弹性地基刚度EFS可以模拟温克尔地基。

由结构振型结果对比，两种情况下低阶模态振型完全一致，因此，弹性地基刚度EFS完全可以模拟弹簧单元地基。基于以上研究分析，这里在水闸闸基脱空参数的识别研究中，采用弹性地基刚度EFS模拟温克尔地基是合理的。