基于格雷编码的遗传算法优化响应面模型拟合

遗传算法在求解反问题时，具有自适应性、智能型等优势，所以得到了广泛的应用。在拟合响应面模型时，这里采用基于格雷编码的遗传算法进行优化求解。遗传算法流程图如图6.1.3所示。

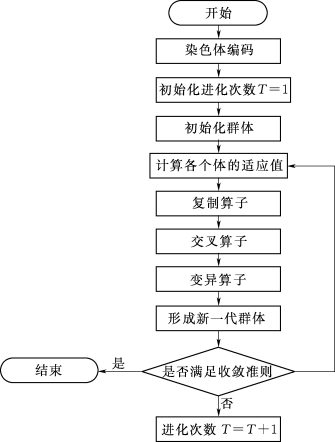
图6.1.3　遗传算法流程图

对于传统的遗传算法，虽然操作简易，容易实现，但是也存在局部搜索能力较差的问题，使得寻优陷入局部最优。采用格雷编码的遗传算法可以提高局部寻优能力。结合图6.1.3，采用格雷编码的遗传算法寻优的基本思路如下：

（1）编码。遗传算法在搜索之前，首先要将解空间的数据转换成遗传空间的基因数据。最初的编码为Holland提出的二进制编码，其简单，利于交叉、变异等特点，但是因其占用内存大、精度不高等特点，使其解决高维数据时具有很大的局限性。而现在的结构越来越倾向于大型化、复杂化，所以针对其局限性，提出了很多改进的方法，如：

1）格雷码编码。若二进制编码为X=xmxm-1…x2x1，其对应的格雷码为Y=ymym-1…y2y1，则

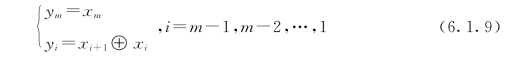
格雷码在二进制编码的基础上提高了算法的局部搜索能力。

2）实数编码。较二进制编码提高了算法的精度。

3）十进制编码。解决了算法的过早收敛问题。(www.xing528.com)

（2）生成初始种群。随机生成一定数目的初始结构数据。若无先验信息，可以随机产生；若有一定的先验性息，可以将先验信息转化为一定的边界条件，提高算法的效率。

（3）适应度函数评价。由目标函数转换而成，最常见的适应度函数：

目标函数最大化

目标函数最小化

（4）算子选择。以优胜劣汰的原则，把优化的个体遗传到下一代，进行下一代的操作。

（5）交叉。父代的部分个体重组成新个体，在算法中交叉算子不仅可以保持原来群体中的优良个体，而且还可以使算法搜索新的基因空间。

（6）变异。针对种群中的单体上的某些基因值的改变。

在实际测试中，模态信息中的频率和振型是较容易获得的，这里将以频率和振型作为遗传算法中目标函数的信息量。考虑到实际水闸可能会出现的脱空形式，首先对脱空区域进行分类，借助脱空控制参数来描述脱空区域，建立响应面模型以取代有限元模型，借助改进的以水闸模态信息为目标函数的遗传算法对水闸底板单侧脱空和多侧脱空的脱空区域进行反演识别研究。