特征量和参数选取的实验设计方法

在运用响应面方法对有限元模型进行修正方面，输入变量通常选取结构的材料特性以及几何特征，比如选取结构的频域特征、时域特征作为结构的输入；结构物理参数的选择主要包括几何尺寸、弹性模量、弹性刚度和阻尼等。考虑安全监测数据获得的难易程度和可行性，本书在水闸底板脱空区域反演识别分析中选取水闸结构的频率和振型数据作为结构的输出响应。

在响应面的建立中，实验设计是一个很重要的部分，实验设计涉及后面的响应面精度。实验样本点的取值，包括样本点的范围、分布和数目，是实验设计的重要内容。目前应用比较广泛的标准实验设计，如中心复合设计、Box-Behnken设计、最优设计等在响应面函数拟合过程中具有很好的精度，但是这些实验设计选择的样本点区域都是规则的立方体，解决标准实验设计非常好，但是遇到不规则实验区域等问题时，其适用性和有效性得到限制。为了合理、全面地表达结构响应与物理参数之间的输入-输出关系，样本点的取值必须在修正参数区间内均匀分布，所以拉丁超立方抽样以其均匀设计的特点取代了众多的标准实验设计方法。这里选用目前应用广泛的拉丁超立方抽样（LHS）技术进行实验设计。对其工作思路做简单介绍：

（1）选取合适的参数和程序运行的抽样数目N。

（2）把每一次输入等概率地分成N列，即

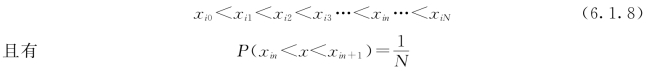(www.xing528.com)

（3）由图6.1.2可知，每一列只抽样一个数据，每一列中抽取的数据位置是不确定的。

拉丁超立方抽样与分层抽样相比，优点是：无论抽样数目的大小，该方法都能较容易地得到样本。

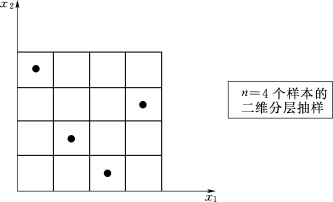
图6.1.2　二维分层抽样图