基于频域分解法的泄流激励模态参数识别：数值模型验证

为验证结构在水流脉动荷载作用下模态参数识别的可行性，建立悬臂梁有限元模型，分别计算悬臂梁结构在水流脉动荷载作用与白噪声荷载作用下的随机响应，而后分别利用各自输出位移响应识别悬臂梁的模态参数，并对各自的识别结果进行对比分析。悬臂梁的物理尺寸及材料参数为：悬臂梁长度L=5.0m，矩形截面尺寸为100mm×120mm，弹性模量E=1.0×1010 N/m2，泊松比μ=0.3，材料密度ρ=2000kg/m3。通过有限元计算的悬臂结构前4阶模态频率见表5.2.1，悬臂梁第1阶振动表现为沿截面短边方向的1阶弯曲振动，悬臂梁第2阶振动表现为沿截面长边方向的1阶弯曲振动，悬臂梁第3阶振动表现为沿截面短边方向的2阶弯曲振动，悬臂梁第4阶振动表现为沿截面长边方向的2阶弯曲振动。

表5.2.1　模态频率识别值与计算值比较

注 识别值后的括号内数值表示与计算值的相对误差。

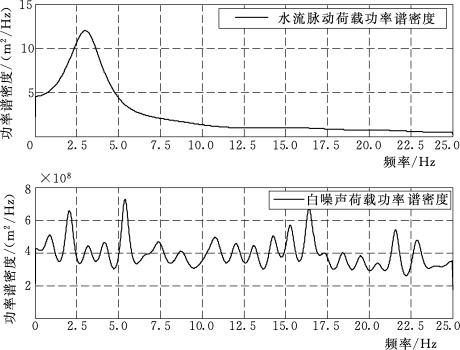
为了能使悬臂梁结构在水流脉动荷载（或白噪声荷载）激励作用下产生多阶振型，施加荷载时沿梁的长度方向分布6个，沿与X、Y轴夹角45°方向施加，如图5.2.3所示。悬臂梁在水流脉动荷载（或白噪声荷载）作用下的瞬态响应计算时间步长取0.01s，计算20.48s共2048个荷载步。水流脉动荷载与白噪声荷载的功率谱密度如图5.2.4所示。

选择悬臂梁截面底部沿长度方向的29个节点Y方向动位移提取结构输出响应，用Welch平均周期法估计输出响应信号的功率谱密度矩阵，取周期长度20.48s（2048个采样点），得到29×29功率谱密度矩阵对其进行奇异值分解，并分别计算典型水流脉动荷载激励下以及白噪声荷载激励下的CMIF指示函数，如图5.2.5和图5.2.6所示。

图5.2.3　荷载沿悬臂梁分布及荷载施加方向

(www.xing528.com)

图5.2.4　水流脉动荷载与白噪声荷载的功率谱密度

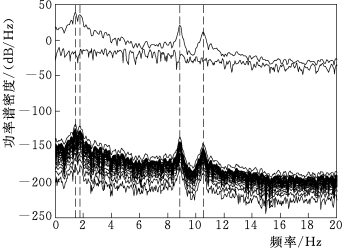
图5.2.5　水流脉动荷载激励下的CMIF指示函数

模态频率位移奇异值曲线各峰值处，无论是水流脉动荷载激励下还是白噪声荷载激励下，从图中可以识别悬臂梁的前4阶模态频率，见表5.2.1。悬臂梁前4阶振型识别值如图5.2.7所示，振型识别结果与计算模态振型吻合较好。

从识别结果来看，无论是白噪声激励还是水流脉动荷载激励，仅利用输出响应均能够较精确地识别结构模态参数，见表5.2.1及图5.2.7，结构在水流脉动荷载激励下的识别值与白噪声激励下的识别值较为接近，且与模态计算值误差很小。可见，结构在水流脉动荷载激励下（即泄流状态），该方法仅利用结构的流激振动响应可以准确地识别结构模态参数。

图5.2.6　白噪声荷载激励下的CMIF指示函数

图5.2.7　悬臂梁前4阶振型识别值