频域分解法的基本原理

5.2.1.1　结构泄流激励响应间的互功率谱函数理论

假设系统的未知输入f（t）和输出x（t）之间的关系可以表示为[85]

式中：Gff（jω）为Ni×Ni阶输入荷载的功率谱密度（PSD）矩阵，Ni是输入点数；Gxx（jω）为No×No阶输出响应的功率谱密度矩阵，No是输出点数；H（jω）为No×Ni阶频响函数（FRF）矩阵，上标H表示复共轭转置。

频响函数矩阵可以表示为部分分式的和，即极点/留数的形式：

式中：N为模态个数；λk为系统极点；为频响函数的k阶留数矩阵，φk、γk分别为模态振型向量和模态参与向量。

假定输入是白噪声，其自功率谱密度矩阵为一个常数矩阵，即Gff（jω）=C，则式（5.2.1）变为

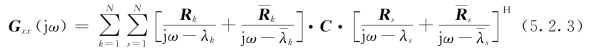
将上式两部分相乘并分解为部分分式的和，则输出的功率谱密度矩阵可以表示为如下极点/留数形式：

式中，Ak为输出响应功率谱密度矩阵的第k阶留数矩阵，它是一个Hermitian矩阵，和输出响应功率谱密度矩阵具有相同的维数No×No，其表达式为

式中，αk为系统极点的负实部。系统极点可表示如下：

Ak可进一步表示为模态振型的形式：

式中：为一标量常数。

通常情况下，一般结构阻尼较小，式（5.2.4）中的前两项将占主导地位，而且对于一个确定的频率ω，仅有限个模态贡献显著，典型的情形是一个或两个模态。记这些对应模态固有频率的集合为Sub（ω），对于小阻尼结构，响应的功率谱密度可以表示为

可以看出，式（5.2.8）与式（5.2.2）的表达式很相似，极点包含了频率和阻尼信息，其中的留数项都同模态振型成比例。

5.2.1.2　识别算法

1.功率谱密度矩阵的奇异值分解

频域分解法首先要估计功率谱密度矩阵，系统在白噪声激励下，由响应测试数据可以得到功率谱密度的估计为在其离散频率ω=ωk处，对）进行奇异值分解可得

式中：为Uk的列向量；Sk=diag为按ski（i=1，2，…，No）降序排列的奇异值。

2.复模态指示函数CMIF

若处只是单个模态的谐振点，则中只有sk1达到最大值。一般的，若处是i个模态共同的谐振点，则ski（i=1，2，…，No）中有i个奇异值在ω→ωk处达到局部最大，若令所有小的和没有达到局部最大的奇异值等于零，则对角矩阵Sk的秩与ωk点的模态数相等，且Uk中与非零奇异值ski相对应的列向量uki是第i阶模态振型。可见，通过矩阵Sk可以辨识结构的模态频率和振型，Sk被称为复模态指示函数（Complex Mode Indicator Function，CMIF）。采用CMIF识别结构频率和振型的基本方法如下：

假设结构有No个实测输出响应（可以是位移或加速度），数据采样频率为Fs，分析数据长度为L。通过互（自）功率谱密度计算可得No×No功率谱矩阵序列其中，K=1，2，…，L/2；Δω=2π·Δf；Δf=Fs/L。由式（5.2.9）可知，对每个k的每个取值对进行奇异值分解得到

将的对角元素整理成No×L/2矩阵，即可得CMIF的离散序列矩阵：

式中，si，K是第i个奇异值的第K次计算结果。CMIF每个行序列s1，s2，…，sNo构成No个奇异值曲线，奇异值的峰值对应于系统的模态。

假设结构的模态数为Ne，则奇异值曲线对应Ne个峰值，相应的模态频率为{Ki·Δω}，Ki∈K为奇异值曲线峰值对应的横坐标。每个奇异值曲线峰值处只存在一个单独的模态，则的第一列是第i阶模态振型。的每个元素对应一个响应测点位置，其幅值代表位移量，相位代表方向。实际计算振型时，可直接根据相位的正、负确定振动位移的方向。振型可按下式计算：

式中：sign（·）为符号函数；angle（·）为求复数的相位；|·|为求复数的幅值。

由以上可知，频域分解法可以直接识别结构的频率与振型，但无法获得结构阻尼比。由于式（5.2.9）的奇异值分解过程将系统的谱函数矩阵分解成了一个个单自由度的谱函数，在此基础上可以用于半功率法得到阻尼比参数。

5.2.1.3　功率谱密度函数的模态频率置信区间（MCF）的确定

在功率谱密度图中，对应r阶模态固有频率ωr处的峰值附近，该阶模态将起主导作用。如果在此处仅有一个模态起主要作用，则的第一列）是第i阶模态振型，对应的奇异值就是相应单自由度系统的自功率谱密度函数，奇异值曲线峰值的选取一般都是凭经验拾取，而且精度取决于计算功率谱密度函数时傅里叶变换的精度。因此必须寻求比较准确的方法确定奇异值曲线的峰值，辨别所拾取峰值是结构真实模态频率还是水流噪声引起的虚假模态频率，并同时确定该阶模态起主要作用的优势频域带宽。本书定义模态一致性指标函数（Modal Coherence Function，MCF）为

(www.xing528.com)

式中：为第i阶模态振型即奇异值向量的第一列；相邻点的奇异值向量，其中K=1，2，…，L/2进行遍历。

MCF计算的是奇异值曲线峰值处模态振型向量与在奇异值峰值曲线附近点的第一列奇异值向量之间的相关关系。如果模态一致性函数在某个频率带宽内等于1或近似等于1，则说明在该频带宽度内，该阶模态频率起主导作用，该频带宽度即为该阶模态的优势频域带宽。根据该阶模态的频率带宽进行傅里叶逆变换，即可得出该单自由度功率谱密度函数的时域波形。

5.2.1.4　阻尼比的计算

1.半功率带法

式（5.2.9）的奇异值分解过程将系统的谱函数矩阵分解成了一个个单自由度的谱函数，在此基础上可以用于半功率法得到阻尼比参数。

对于一个单自由度结构振动体系，结构的位移频响函数H（ω）可表示为

式中：m为结构质量；（k为结构刚度）为结构的固有圆频率；（c为结构阻尼）为结构的临界阻尼比。

频响函数H（ω）为复数，可用幅值-相位的方程表达，即

式中：|H（ω）|与θ（ω）分别为频响函数的幅值和相位，其可表达为

式（5.2.16）所述的单自由度结构的幅频特性曲线如图5.2.1所示，为求幅频特性曲线值所对应的圆频率ω′0，令

由式（5.2.19）解得

代入式（5.2.16）得

一般工程结构阻尼比ξ很小（ξ≤0.1），则

可见，由幅频特性曲线峰值所对应的频率可确定结构的自振圆频率。为确定结构的阻尼比，考察半功率点处所对应的频率值，即满足方程

方程（5.2.23）的两个解为

式（5.2.27）为确定结构阻尼比的半功率点法。

图5.2.1　单自由度结构的幅频特性曲线

2.半功率带法的改进

对于小阻尼系统，用传统半功率点法识别，通常就认为离散谱线中明显尖锐的谱峰对应固有频率，操作较为方便。但实际上用半功率点法会遇到以下两种情形：①与局部谱峰左右相邻的两条谱线均小于半功率数值；②局部最大值左右的谱线远远偏离对称状态，一侧有超过半功率的谱线，而另一侧临近的谱线均远远小于半功率点。这两种情形均使传统半功率点的确定有困难，文献[86]用线性插值的方法确定半功率点，大大降低了阻尼比的识别误差。其基本原理如下：

设已经找到幅值的局部最高谱线频率为f0，幅值为G0，而FFT的谱线间隔为Δf。左边半功率点位于f1和f2之间（f2=f1+Δf），右边半功率点位于f3和f4之间（f4=f3+Δf）。f1～f4的对应幅值分别为G1～G4。通过线性插值确定半功率带宽，首先应确定图5.2.2中左半功率点和右半功率点所对应的频率fa、fb。左边两条谱线f1和f2顶端的直线方程为

图5.2.2　线性插值法确定半功率点示意图

线性插值左边半功率点满足方程

由此可得线性差值半功率带宽为

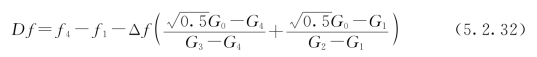
则估计的阻尼比ξ=Df/（2f0）为

如果f1和f4恰好为半功率点，则式（5.2.33）就回到普通的半功率点法。