小波阈值降噪方法优化

小波阈值降噪方法的基本思想是对含噪声信号f（t）作小波分解后的各层系数中，对大于和小于某一阈值的小波系数分别进行处理，然后再利用处理后得到的小波系数重构原信号，达到降噪的目的。

设ωj，k是观测信号f（t）的小波系数，记为ω。η（ω）表示阈值处理后的系数，即阈值函数，表示对ω的模大于或小于阈值T的不同处理结果。在阈值降噪方法中，有两个关键问题：一是阈值函数的选取；二是对阈值的具体估计。

4.1.3.1　阈值函数的选取

常用阈值函数有硬阈值函数和软阈值函数。硬阈值函数[图4.1.1（a）]：

软阈值函数[图4.1.1（b）]：

这两种阈值函数在实际中经常使用，也取得了较好的效果。但方法本身也存在着一些缺点，如硬阈值函数方法在ω=T，η（ω）不连续，用η（ω）重构信号时会产生振荡；软阈值函数方法得到的η（ω）虽然连续性好，但在|ω|＞T时，η（ω）与ω存在着恒定偏差，直接影响重构信号的性质。因此为了克服上述阈值函数的一些缺点，有必要对阈值函数进行一些改进，常用的效果较好的阈值函数有：

（1）由多项式插值法构造：

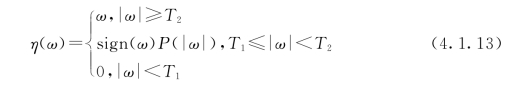
式中，P（|ω|）为插值多项式，可取一次、二次或三次多项式。其插值条件分别为

(www.xing528.com)

式（4.1.13）表示的阈值函数克服了硬阈值函数在点T处不连续，软阈值函数在|ω|较大时，η（ω）与ω总有一定偏差的缺点，因而使得降噪效果比较理想，但要估计两个阈值T1、T2比较困难。

（2）软、硬阈值折中法构造：

折中法构造的阈值函数如图4.1.1（c）所示，当λ=0和1时，式（4.1.15）就成为硬阈值函数和软阈值函数。当0＜λ＜1时，η（ω）的值介于软、硬阈值函数得出的值之间，因而这种阈值函数降噪效果较好。它使得η（ω）的值更接近原信号的小波变换值，并通过调整λ值以获取更好的降噪效果。

图4.1.1　阈值函数

4.1.3.2　阈值的估计

对阈值的具体估计是关系到信号降噪效果的一个关键问题，阈值太小，达不到降噪效果，阈值太大，信号的一些重要特征又将被虑掉，重构信号会引起偏差。阈值的估计比较复杂，常用的一种简单估计为

式中：σ为噪声的标准方差；N为信号的长度。

在实际应用过程中，T值的估计应是自适应的，即应考虑到信号的相对平稳性和信噪比的大小。对于平稳性较差的信号，T值应取得小一些，相反情况T值应取得较大。对于同一信号，信噪比大时，噪声功率小，则T值可取得小些。