以一泄水槽中的悬臂板(模拟闸墩)为例,基于本方法对结构进行传感器优化,通过建立室内试验模型,按优化配置结果进行布点,并以此为前提开展基于泄流激励下的结构模态参数识别模型试验。悬臂梁结构尺寸(高×宽×厚)为50cm×25cm×4cm,材料参数为:ρ=1650kg/m3,E=9.5×106 N/m2,μ=0.47。建立三维实体有限元模型,结构共有450个单元,768个节点,每个结点有三个自由度(分别为Ux、Uy、Uz),模型底端固定,进行有限元模态求解后,可得到该模型模态振型。
模态分析结果表明,前6阶主要表现为悬臂梁的侧向振动或侧向扭振,第7阶以后表现为垂向拉伸或高阶弯曲振动,考虑到悬臂梁在泄流激励下的振型主要是以低阶侧向振动为主,因此本试验动力测试也主要以梁的侧向振动(即Uz向)测试为主,故进行传感器优化时,将悬臂梁侧面上的节点Uz方向视为可布置传感器测点集合(即可量测点),共240个自由度,选取前6阶模态进行优化布点研究。
悬臂梁侧面Uz方向的240个自由度MAC矩阵柱状图如图3.4.1所示,QR分解后得到的初始配置(6个自由度)的MAC矩阵柱状图如图3.4.2所示,QR分解后选取的初始测点位置图如图3.4.3所示,优化选点后的12个自由度MAC矩阵柱状图如图3.4.4所示。

图3.4.1 悬臂梁侧面Uz方向的240个自由度MAC矩阵柱状图

图3.4.2 QR分解后得到的初始配置(6个自由度)的MAC矩阵柱状图
图3.4.5为在经QR分解后选取的初始位置中每增加一个自由度时MAC矩阵最大非对角元的变化曲线,可以看出,曲线呈逐渐下降直至趋于稳定,说明增加一定的测点后剩余测点对动力测试的贡献不大,当增加15个自由度时,即选取悬臂梁模型21个自由度时能达到最优化效果,但此时所需传感器数量仍然过多,经济上不合理,综合最大非对角元曲线变化,在初始配置中增加6个传感器就可达到很好的优化效果,因此选取12个自由度作为该悬臂梁结构传感器的最终配置。传感器最终配置测点位置图如图3.4.6所示。

图3.4.3 QR分解后选取的初始测点位置图
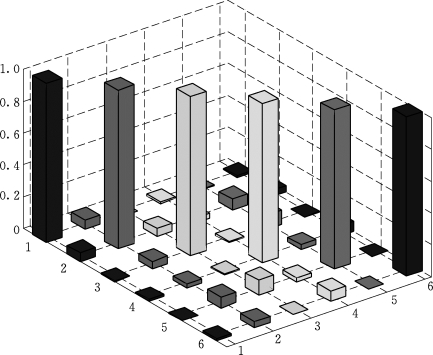
图3.4.4 优化选点后的12个自由度MAC矩阵柱状图
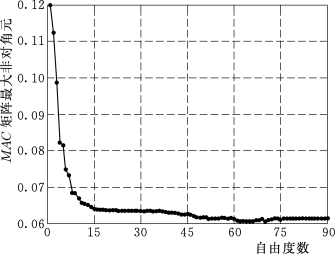
图3.4.5 MAC矩阵最大非对角元的变化曲线
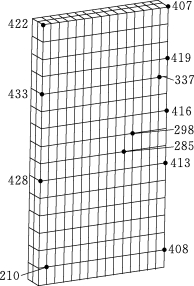
图3.4.6 传感器最终配置测点位置图(https://www.xing528.com)
最终选取的12个自由度见表3.4.1,其中前6个自由度为QR分解的结果,各测点在结构上的位置如图3.4.6所示(图中数字为有限元节点编号),表3.4.2为各方案下MAC矩阵的最大非对角元。
从表3.4.2中可以看出,最终选取的12个自由度的MAC矩阵最大非对角元仅为0.075,结果较优。
表3.4.1 悬臂梁结构传感器最优配置

表3.4.2 各种传感器配置的MAC矩阵最大非对角元

泄水槽中的悬臂梁实体模型如图3.4.7所示,依据优化配置方案共布置传感器10个(节点210和节点408处于水下部位,故未布置传感器),传感器采用东华DH107型压电式加速度传感器(频响范围0.5~6000 Hz),信号的采集与处理采用DHDAS动态信号采集分析系统,测试系统的连接与采集如图3.4.8所示。

图3.4.7 泄水槽中的悬臂梁实体模型

图3.4.8 测试系统的连接与采集
典型测点(416节点)加速度原始动态信号及降噪后信号时程如图3.4.9所示。以采集的动态信号为基础,采用基于奇异熵定阶的ERA模态参数识别方法进行模态识别(详见5.1.2节),降噪后的信号以及模态识别结果如图3.4.9及表3.4.3所示,结果表明,识别结果与计算值较吻合。
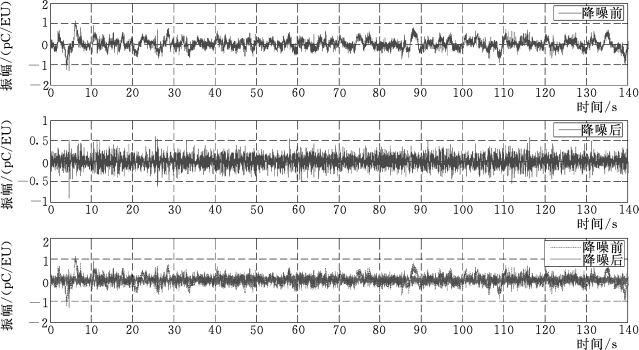
图3.4.9 典型测点(416节点)加速度原始动态信号及降噪后信号时程
表3.4.3 悬臂梁结构模态识别与有限元计算结果对比

免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




