多自由度系统复模态分析优化

实模态分析中，认为振动系统中各点的振动相位差为0°或180°，无阻尼或比例阻尼的振动系统满足此条件。对实模态分析而言，模态系数φ为实数。但实际结构往往都是有阻尼的，而且并非都是比例阻尼，因此结构振动时，各点除了振幅不同外，相位亦不尽相同，即相位差不一定是0°或180°，模态系数成为复数，即形成复模态。

对于实模态分析，阻尼矩阵定义为质量矩阵和刚度矩阵的线性组合，因此通过与模态振型矩阵的坐标变换运算可以使其转化为对角矩阵。而对于黏性阻尼的一般情况，采用无阻尼的固有振型模态矩阵的坐标变换运算不能使阻尼矩阵对角化，即阻尼矩阵不能在N维主空间解耦，因此采用状态空间法来建立系统的运动方程，可以找到方程的解耦途径。

假设黏性阻尼力与速度成正比，因此运动方程为

将式（2.2.51）与式（2.2.52）联立，并以矩阵的形式表示，可得

令称为状态向量。式（2.2.53）可改写为

式（2.2.54）称为状态方程。考虑自由振动情况，则式（2.2.45）为

式中都为2N×2N阶矩阵。

设式（2.2.55）的解为

式中，Ψ=[ψ1 ψ2 … ψN]T，代入式（2.2.55），可得

求解式（2.2.57），可得2N个复特征值和特征向量，分别记为

特征值：

特征向量：

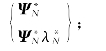
对第r阶模态，其特征值与特征向量分别为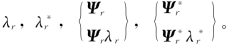

令则式（2.2.57）可写成

对第r阶模态则有

将上式左乘则有

利用A′、B′矩阵的对称性，有；将式（2.2.60）减式（2.2.59）可得

当λr≠λs时，则

将式（2.2.53）代入式（2.2.51）可得

式（2.2.62）和式（2.2.63）即为复模态的正交性条件，由于是2N维向量，因此复模态是在2N维复特征空间中正交，与实模态正交条件不同（实模态是在N维主空间中正交）。

当r=s时，可得

对全部模态而言，模态矩阵为

特征矩阵为

将模态向量中的共轭部分分别排列，可得

因此，对全部模态而言，正交性条件可由下式表示：

当r=s时，由式（2.2.59）可得

式中，由于A′为满秩矩阵，特征向量矩阵Ψ亦为满秩矩阵，因此ar亦为满秩矩阵，故

以上各式中，λr（r=1，2，…，N）为系统的复模态频率；为系统的复模态向量或复振型系数向量，为2N×1维向量。λr及均为复数，均共轭成对，都是系统的复模态参数。下面对复模态振型进行分析。

对状态向量用复模态坐标进行变换，可得

式中：Q、Q*为复模态坐标。

将式（2.2.71）代入状态方程（2.2.55），同时左边乘由正交性条件，得

式（2.2.72）说明系统在以特征向量为基向量的2N维复状态空间中是解耦的。

对第r阶模态，则有(www.xing528.com)

式中：qr为第r阶复模态坐标。

式（2.2.73）和式（2.2.74）的解分别为

对于全部模态而言，则有

式中：分别为t=0时的模态坐标向量及其共轭。

将式（2.2.77）代入式（2.2.71）并取向量的上半部，可得

同理可得速度响应向量：

对l点的瞬时位移则可写成：

式中，ψlr、λ、qr0均为复数，可用模与相角表示。设

式中：ηlr、pr为第r阶模态下l点的模态系数及模态坐标的幅值；γlr、θr分别为它们的相角；αr、βr为复模态频率的实部及虚部。

将式（2.2.81）～式（2.2.83）代入式（2.2.80），整理得到

式（2.2.84）即为复模态自由振动的解，它表明系统在复模态时的自由响应为N个复响应的叠加。可见，复模态时，系统第l点响应不仅具有幅值，而且有相位，不同点的相位是不同的。假设系统只有1阶模态，则各点响应列向量为

因此，系统各点的响应不仅幅值不同，而且相位也不同，这就形成了复模态不同于实模态的运动特性。

2.2.5.1　复模态特性

（1）复共轭特性。复模态时，系统的特征值与特征向量均为复数，而且共轭成对，共有2N个复特征值，即λ1，λ2，…，λN，λ*1，λ*2，…，λ*N，相应的有2N个复特征向量，即

（2）正交性。复模态时，在以复特征向量为基向量所张成的2N维空间中正交，而实模态则在N维主空间中正交。

（3）解耦性。对复模态而言，系统的运动微分方程在复特征向量所张成的2N维状态空间中解耦，而实模态则在N维主空间中解耦。

（4）运动特征。复模态时，系统呈现一些与实模态不同的运动特点，主要有：

1）复模态时，系统各点的相位不同，存在着相位差，且无一定规律；而对于实模态，各点间的相位差为0°或180°。

2）由于复模态时各点运动有一时间差异，因此它们不同时通过振动的平衡位置；而对于实模态，各点同时通过振动平衡位置。尽管如此，对于复模态而言，各点的振动频率和周期仍然相同，由βr决定，对一定模态而言它是常数。

3）对复模态，系统振动时，无一定振型，节点亦不一定是固定的，而作周期性移动。这与实模态截然不同。

4）复模态的自由振动是衰减振动，而且各点的衰减率相同，衰减率由αr表示，与实模态相同。

2.2.5.2　复模态传递函数表达式

由式（2.2.54）和式（2.2.72）可得

对第r阶模态，可写成

式（2.2.87）的解可由Duhamel积分求得

式（2.2.88）和式（2.2.89）中等式后边的第一项相当于自由振动解，第二项则相当于受迫振动解。

设初始状态（t=0）为振动平衡位置，即，则系统受迫振动的响应向量由式（2.2.71）可写成

对式（2.2.90）两边作拉氏变换，得

因此，传递函数矩阵为

式中：Ar、A*r为留数矩阵及其共轭。

令s=jω，则系统的频响函数矩阵为