运动微分方程简介

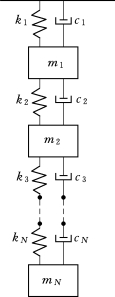
图2.2.1　多自由度线性定常系统

以N自由度的比例阻尼系统作为研究对象，如图2.2.1所示的多自由度线性定常系统，其运动微分方程为[78]：

式中：M、C、K分别为系统的质量、阻尼和刚度矩阵。通常M及K为实系数对称矩阵，而其中质量矩阵M是正定矩阵；刚度矩阵K对于无刚体运动的约束系统是正定的，对于有刚体运动的自由系统是半正定的。当阻尼为比例阻尼时，阻尼矩阵C为对称矩阵。M、C、K均为N×N阶矩阵。X和F分别为系统各点的位移响应向量及激励力向量。

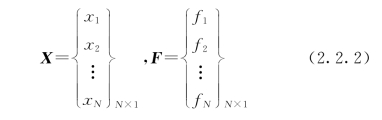
式（2.2.1）是用系统的物理坐标X、X·、X··描述的运动方程组。在其每一个方程中均包含系统各点的物理坐标，因此是一组耦合方程。当系统自由度数很大时，求解十分困难。能否将上述耦合方程变成非耦合的、独立的微分方程组，就是模态分析所要解决的根本任务。模态分析方法就是以无阻尼系统的各阶主振型所对应的模态坐标来代替物理坐标，使坐标耦合的微分方程组解耦为各个坐标独立的微分方程组，从而求出系统的各阶模态参数。这就是模态分析的经典定义。

对式（2.2.1）两边进行拉氏变换，可得

式中：s为拉氏变换因子；X（s）、F（s）分别为位移响应与激励力的拉氏变换（初始条件为零），即

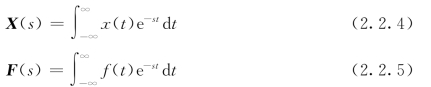
式（2.2.3）又可写为

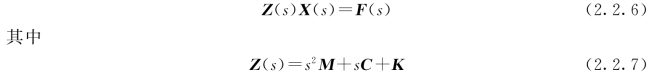
式中：Z（s）为位移阻抗矩阵，为N×N阶矩阵。

阻抗矩阵Z（s）的逆矩阵称为传递函数矩阵：

对线性时不变系统，其极点在复平面左半平面，因此可将s转换成jω，便可得出在傅氏域中的阻抗矩阵及频响函数矩阵：(www.xing528.com)

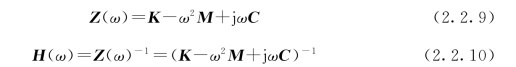
此时，系统的运动方程为

由振动理论知，对线性时不变系统，系统的任一点响应均可表示为各阶模态响应的线性组合。对l点的响应可表示为

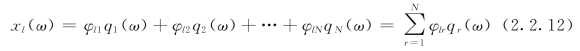
式中：φlr为第l个测点、第r阶模态的振型系数。

由N个测点的振型系数所组成的列向量为

式中：φr为第r阶模态向量，它反映该阶模态的振动形状。由各阶模态向量组成的矩阵称为模态矩阵，记为

式中：Φ为N×N阶矩阵。

式（2.2.12）中的qr（ω）为第r阶模态坐标。其物理意义可理解为各阶模态对响应的贡献量，其数学意义可理解为加权系数。各阶模态对响应的贡献量或权系数是不同的，它与激励的频率结构有关。一般低阶模态比高阶模态有较大的权系数。

由式（2.2.12）与式（2.2.14）可得系统的响应列向量为

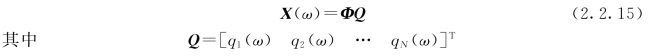
将式（2.2.15）代入式（2.2.11），得

下面分别对几种情况进行讨论。