脉动压力的谱密度及类型

泄流脉动荷载一般可用概率方法和描述随机数据的统计函数描述。以p（t）表示某点脉动压力，在平稳、各态历经性假定下，可用功率谱密度函数G（f）（简称谱密度）表征p（t）的频率结构：

式中：p（t，f，Δf）为p（t）在f至f+Δf频率范围内的分量。

G（f）定义在（0≤f＜∞）频率域，称单边谱密度。双边谱密度S（f）定义在（-∞，+∞）频率域，与G（f）有如下关系：

p（t）的自相关函数R（τ）与G（f）互为傅里叶变换，即

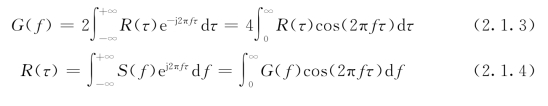
p（t）的均方值ψ2与G（f）有如下关系：

p（t）的均值也可以由谱密度G（f）求得：

式中：积分下限0-表示从下面接近0；积分上限0+表示从上面接近0。

式（2.1.6）表明，p（t）的均值等于G（f）中零频处δ函数曲线下面积的正平方根。

当p（t）具有零均值，即μ=0时，显然均方值等于方差σ2，由式（2.1.5）可知，这时：(www.xing528.com)

σ2的正平方根称标准差，表征脉动压力的平均强度。脉动压力的相对强度常用σ/μ或[（σ/γ）/（v2/2g）]表示，后者常用β表示，称为压强系数，即

p（t）的取值规律可用概率密度函数描述。在许多泄流条件下可假定p（t）为正态分布。p（t）的正态概率密度函数为

以上可知，只要知道某点p（t）的谱密度G（f）或S（f），便可求出G（f）或S（f）有关的p（t）其他统计函数，进而分析p（t）的统计特性。因而，谱密度G（f）或S（f）是描述p（t）特征的最重要的统计参数之一。

可以设想泄流的脉动压力由许多具有一定能量的频率分量组成，谱密度的物理意义即表征组成p（t）的这些频率分量所具有的平均能量大小。由于不同泄流条件下构成p（t）的频率分量不同，各频率分量具有的能量大小及其在总能量中所占比重不同，在不同泄流条件下p（t）的G（f）也不同。即使在同一泄流条件下，不同点处p（t）的G（f）也有区别。大量原型观测资料分析表明，水流脉动压力的谱密度G（f）从频率域能量分布结构考察，基本可分为下列四种类型[50]：

（1）有限带宽的近似白噪声谱——脉动压力的能量在有限带宽内近乎均匀分布，如图2.1.1（a）所示。

（2）宽带噪声谱——频带宽，脉动能量在频带内分布比较均匀，没有十分突出的能量集中区，如图2.1.1（b）所示。

（3）具有优势频率的宽带噪声谱——频带较宽，脉动能量在整个频带内分布较均匀，但有明显、突出的能量集中区，如图2.1.1（c）所示。

（4）窄带噪声谱——频带较窄或脉动能量特别集中在一个或几个狭窄的频区，谱密度在这些狭窄频区上有突出的峰值，如图2.1.1（d）所示。

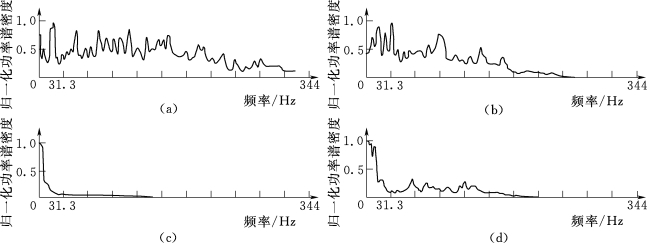
图2.1.1　脉动压力的谱密度类型

由于脉动结构是有尺度的，当水流内部包含以某种瞬间速度运动的大小不等的各种尺度脉动结构时，在谱密度图上则表现为频带较宽，各频率分量的能量基本接近或大致相等，脉动能量在频带内的分布较均匀，没有十分突出的能量集中区，此类脉动压力谱密度常为近似白噪声谱或宽带噪声谱。当水流内部包含多种尺度的脉动结构，且脉动结构中存在能量相对较大而明显占优势的频率分量时，在谱密度图上则表现为频带较宽，脉动能量在频带内的分布较均匀，但有明显、突出的峰值，此类脉动压力谱密度常为具有突出优势频率的宽带噪声谱。当水流内部仅以某种尺度的脉动结构为主时，在谱密度图上表现为脉动能量主要集中在狭窄的一个或几个区域，且在这些狭窄的频区上有突出的峰值，此类脉动压力谱密度常为窄带噪声谱。一般情况下，闸坝泄流结构的脉动压力谱密度均属于上述四种基本谱型中的一种或某几种的组合。