网格是构成有限元分析模型的重要组成元素,也是有限元分析计算的基础。网格的划分是将理想化模型拆分成有限数量的区域,这些区域被称为【单元】,单元之间由节点连接在一起。
1.网格类型
按网格单元的测量方法进行划分,Simulation可以创建如下网格类型。
●3D四面实体单元,如图9-39所示。
●2D三角形壳体单元,如图9-40所示。
●1D横梁单元,如图9-41所示。
按网格单元形状进行划分,Simulation中有四种单元类型:一阶实体四面体单元、二阶实体四面体单元、一阶三角形壳单元和二阶三角形壳单元。在SolidWorks Simulation中,称一阶单元为【草稿品质】单元,二阶单元为【高品质】单元。

图9-39 CAD模型和3D四面实体单元
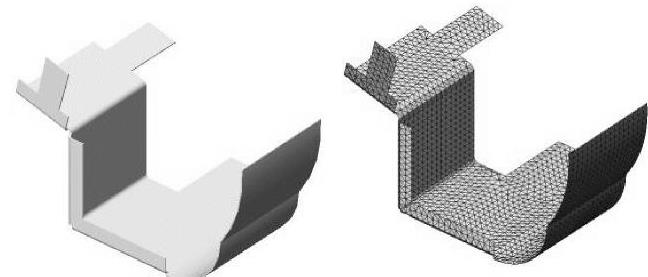
图9-40 CAD钣金模型和2D三角形壳体单元
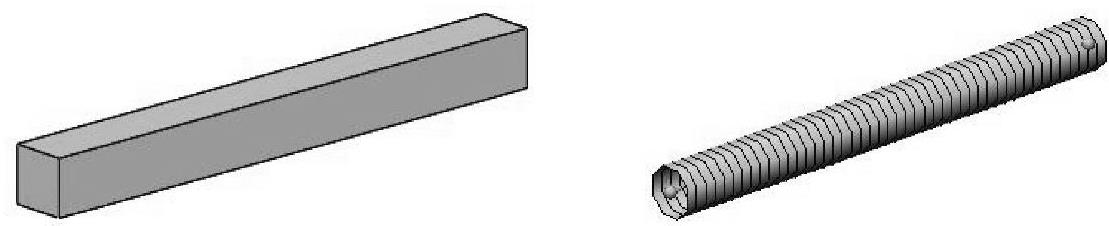
图9-41 横梁CAD和1D横梁单元
技巧点拨
线性单元也称作一阶或低阶单元。抛物线单元也称作二阶或高阶单元。
由于二阶单元具有较好的绘图能力和模拟能力,推荐用户对最终结果和具有曲面几何体的模型使用高品质选项,Simulation默认选择即为高品质。在进行快速评估时,可以使用草稿品质网格化,以缩短运算时间。
线性四面单元由四个通过六条直边线连接的边角节来定义。抛物线四面单元由四个边角节、六个中侧节和六条边线来定义。图9-42为线性和抛物线四面实体单元的示意图。
图9-43为一阶、二阶的线性和抛物线三角形壳体单元的示意图。
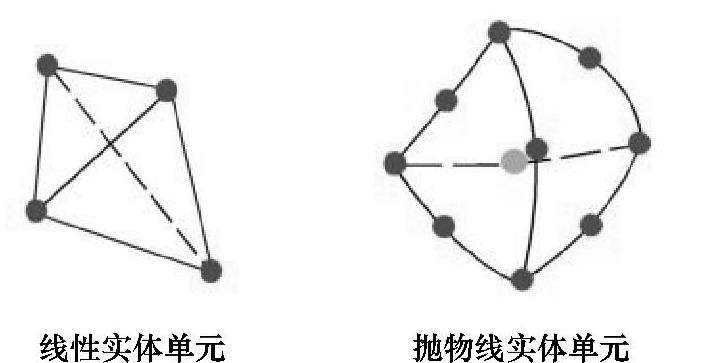
图9-42 一阶与二阶实体单元
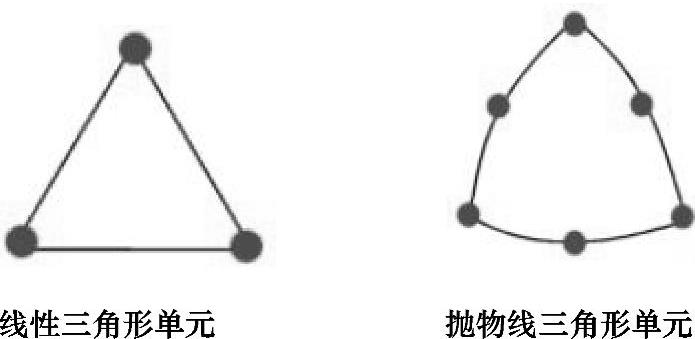
图9-43 一阶与二阶的壳体单元
2.网格划分注意事项(https://www.xing528.com)
我们在划分网格时,需要注意以下几个方面的问题。
(1)网格密度
有限元方法是数值近似算法,一般情况下,网格密度越大,其计算结果与精确解的近似程度越高。但是,在已经获得比较精确计算结果的情况下,再加大网格密度并没有实际意义。
一般而言,网格密度(单元数)相同时,抛物线单元产生的结果的精度高于线性单元,原因如下。
●它们能更精确地表现曲线边界。
●它们可以创建更精确的数学近似结果。不过,与线性单元相比,抛物线单元需要占用更多的计算资源。
对于不同的研究对象,其单元格长度的取值是不同的。确定单元格长度可采用如下3种方法。
●数据实验法,分别输入不同的单元格相比较,选取计算精度可以达到要求,且计算时间较短、效率较高,收敛半径的单元格长度最小,这种方法较复杂,往往用于无同类数据可参考的情况。
●同类项比较法,借鉴同类产品的分析数据。比如,在对摩托车铝车轮进行网格划分时,可以适当借鉴汽车铝车轮有限元分析时的单元格长度。
●根据研究对象的特点,结合国家标准规定的要求,与实验数据相结合。比如,对车轮有限元分析模型,有许多边界参数可参考QC/T212-1996标准的要求,同时结合铝车轮制造有限公司的实验数据取得。
(2)网格形状
对于平面网格而言,可以选择三角形网格和抛物线网格。对于三维网格,可以选择的网格形状有四面体与混合网格。选择网格形状,很大程度上取决于计算所使用的分析类型。例如,线性分析和非线性分析对网格形状要求不一样,模态分析和应力分析对网格形状的要求也不同。
(3)网格维数
在网格维数方面,一般有三种方案可供选择。一是线性单元,有时也称为低阶单元。其形函数是线性形式,表现在单元结构上,可以用是否具有中间节点来判断是否是线性单元。无中间节点的单元即线性单元。在实际应用中,线性单元的求解精度一般来说不如阶次高的单元,尤其是要求峰值应力结果时,低阶单元往往不能得到比较精确的结果。第二种是二次单元,有时也称为高阶单元。其形函数是线性形式,表现在单元结构上,带有中间节点的单元即二次单元。如果要求得到精确的峰值应力结果,高阶单元往往更能够满足要求。而且,一般来说,二次单元对于非线性特性的支持比低阶单元要好,如果求解涉及较复杂的非线性状态,则选择二次单元可以得到更好的收敛特性。第三种是选择所谓的p单元,其形函数一般是大于2阶的,但阶次一般不会大于8阶。这种单元应用局限性较大,这里就不详细讲述了。
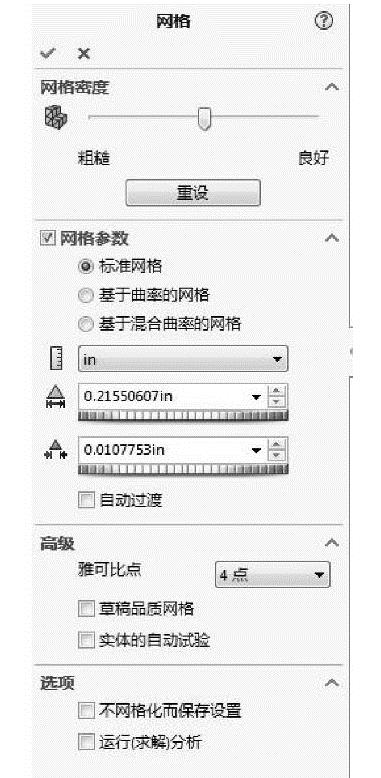
图9-44 【网格】属性面板
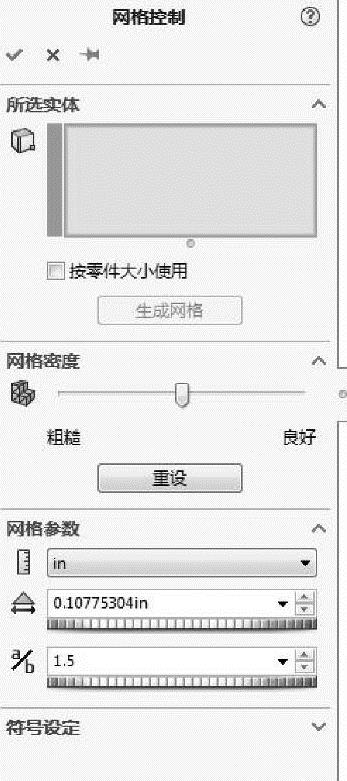
图9-45 【网格控制】属性面板
3.网格划分工具
若要创建网格,可以在菜单栏中执行【Simulation】|【网格】|【生成】命令,或者在Simulation算例树中,右击【网格】项目并选择【生成网格】命令,即可打开【网格】属性面板,如图9-44所示。
如果需要在模型中创建不同单元大小的网格,可以使用【应用网格控制】工具,打开如图9-45所示的【网格控制】属性面板。可以选择模型上的面、边线、顶点或装配体中的某个零组件,分别设置不同的网格密度。
下面通过上机实践操作来演示如何创建1D横梁单元和2D壳体单元,两个实例的源模型相同。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




