了解有限元法：概述与应用

在机械工程中，有限元法已经作为一种常用的方法被广泛使用。计算零部件的应力、变形和进行动态响应计算及稳定性分析等都可用有限元法，如进行齿轮、轴、滚动轴承及箱体的应力、变形计算和动态响应计算，分析滑动轴承中的润滑问题，焊接中残余应力及金属成型中的变形分析等。

有限元法的计算步骤可归纳为以下三个基本步骤：网格划分、单元分析、整体分析。

1.网格划分

有限元法的基本做法是用有限个单元体的集合来代替原有的连续体。因此，首先要对弹性体进行必要的简化，再将弹性体划分为有限个单元组成的离散体。单元之间通过节点相连接。由节点、节点连线和单元构成的集合称为网格。

通常把三维实体划分成四面体（4节点）或六面体单元（8节点）的实体网格，如图9_-1所示。将平面划分成三角形或四边形单元的面网格，如图9-2所示。

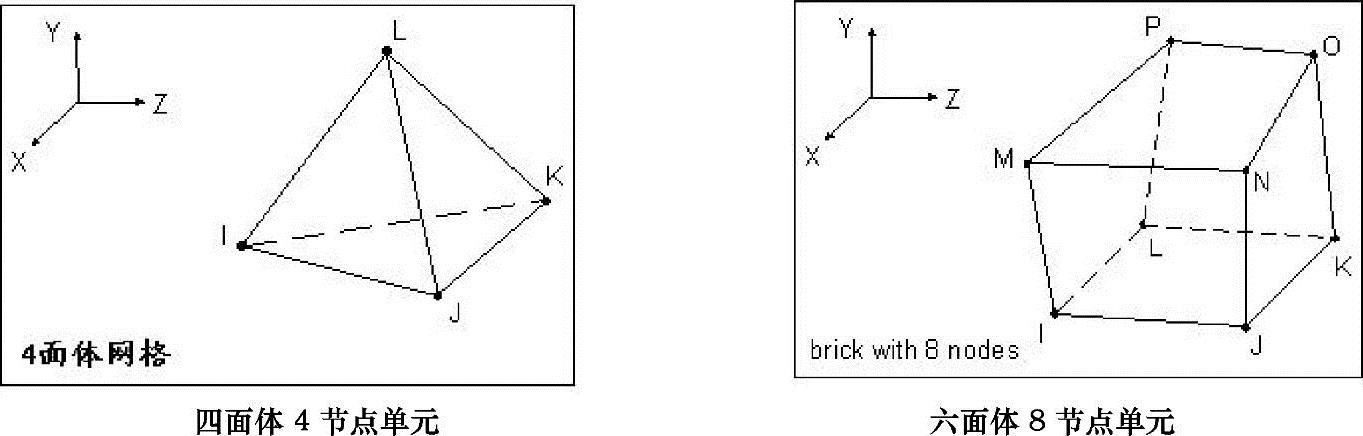
图9-1 实体网格与单元

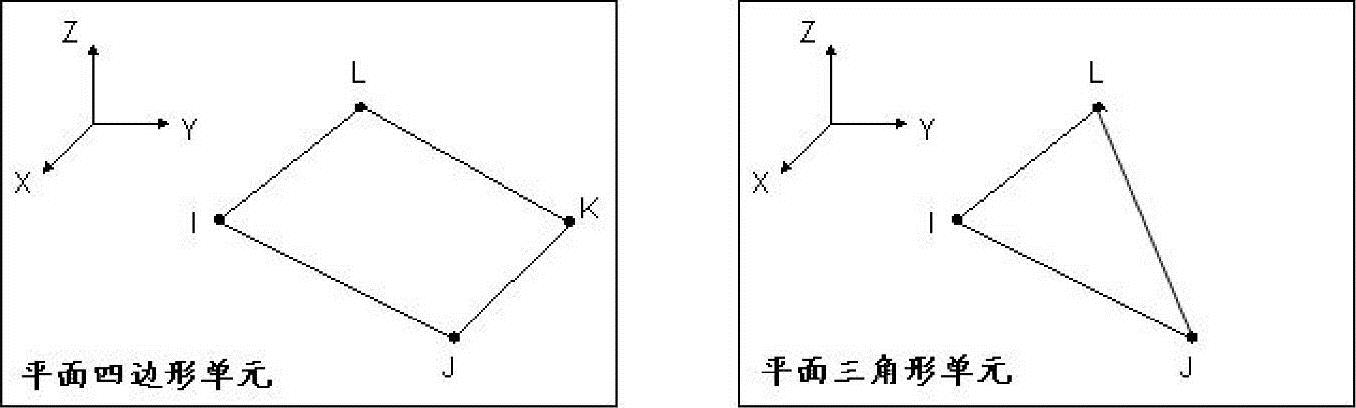
图9-2 平面网格单元

2.单元分析

对于弹性力学问题，单元分析就是建立各个单元的节点位移和节点力之间的关系式。

由于将单元的节点位移作为基本变量，进行单元分析首先要为单元内部的位移确定一个近似表达式，然后计算单元的应变、应力，再建立单元中节点力与节点位移的关系式。

以平面三角形3节点单元为例，单元有三个节点I、J、M，每个节点有两个位移u、v和两个节点力U、V，如图9-3所示。

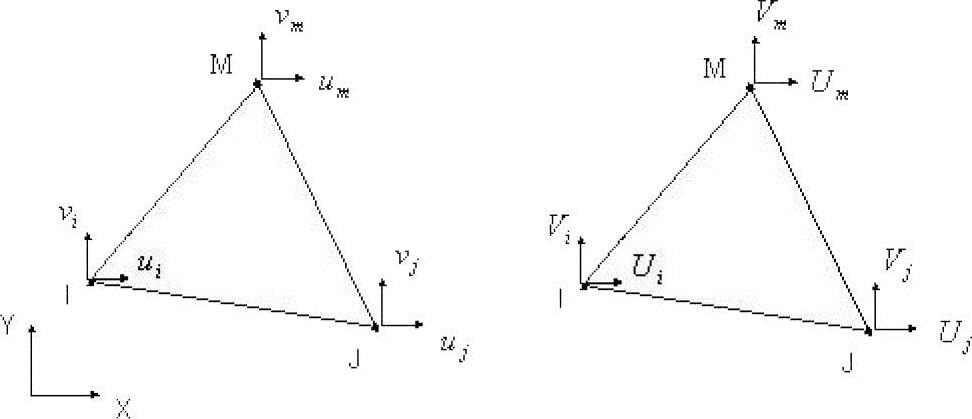
图9-3 三角形3节点单元

单元的所有节点位移、节点力，可以表示为节点位移向量（vector）。

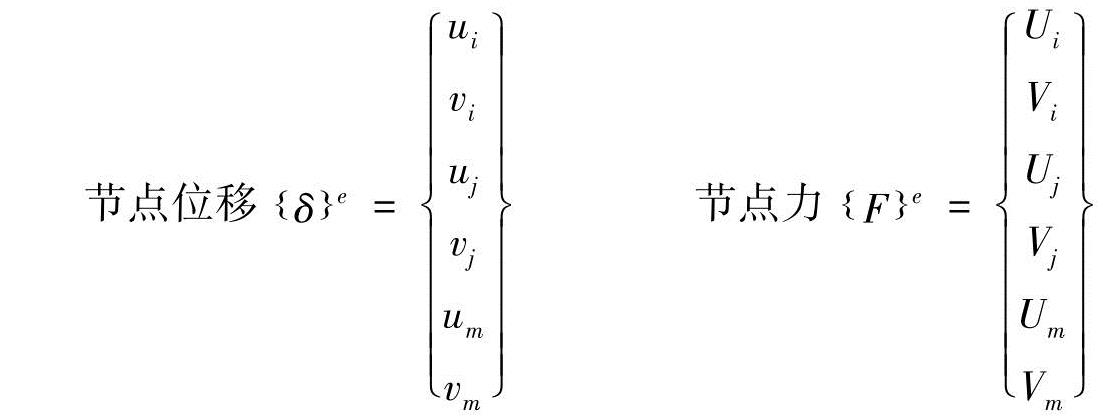
单元的节点位移和节点力之间的关系用张量（tensor）来表示。

{F}^e=[K]^e{δ}^e

3.整体分析

对由各个单元组成的整体进行分析，建立节点外载荷与节点位移的关系，以解出节点位移，这个过程称为整体分析。同样以弹性力学的平面问题为例，如图9-4所示，在边界节点i上受到集中力P_xⁱ、P_yⁱ作用。节点i是三个单元的结合点，因此要把这三个单元在同一节点上的节点力汇集在一起建立平衡方程。

i节点的节点力：

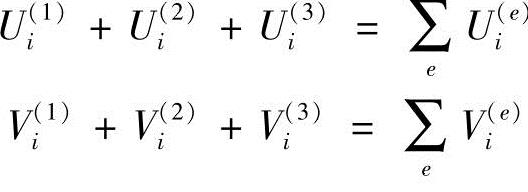(www.xing528.com)

i节点的平衡方程：

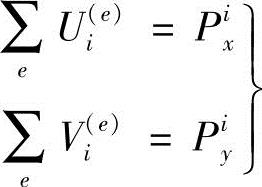
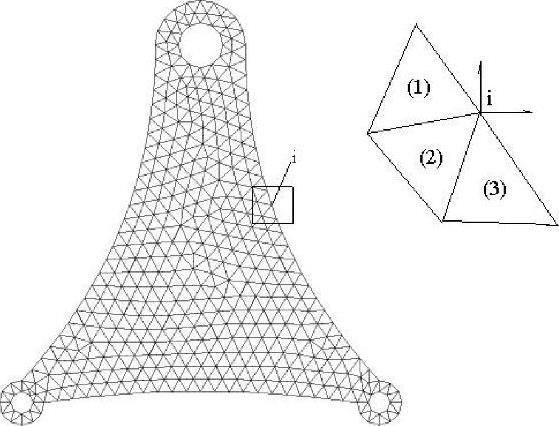
图9-4 整体分析

4.等效应力（也称为von Mises应力）

由材料力学可知，反映应力状态的微元体上剪应力等于零的平面，定义为主平面。主平面的正应力定义为主应力。受力构件内任一点，均存在三个互相垂直的主平面。三个主应力用σl、σ2和σ3表示，且按代数值排列，即σl＞σ2＞σ3。von Mises应力可以表示如下。

在Simulation中，主应力被记为P1、P2和P3，如图9-5所示。在大多数情况下，使用von Mises应力作为应力度量。因为von Mises应力可以很好地描述许多工程材料的结构安全弹塑性性质。P1应力通常是拉应力，用来评估脆性材料零件的应力结果。对于脆性材料，P1应力较Von Mises应力能更恰当地评估其安全性。P3应力通常用来评估压应力或接触压力。

Simulation程序使用von Mises屈服准则计算不同点处的安全系数，该标准规定当等效应力达到材料的屈服力时，材料开始屈服。程序通过在任意点处将屈服力除以von Mises应力而计算该处的安全系数。

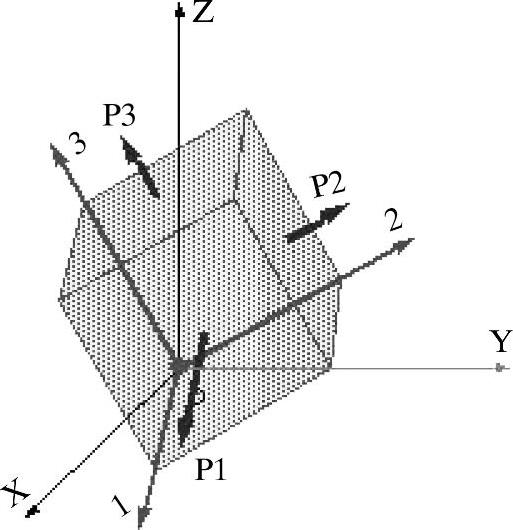
图9-5 主应力图解

安全系数值的解释如下。

●某位置的安全系数小于1.0表示此位置的材料已屈服，设计不安全。

●某位置的安全系数等于1.0表示此位置的材料刚开始屈服。

●某位置的安全系数大于1.0表示此位置的材料没有屈服。

5.在机械工程领域内可用有限元法解决的问题

（1）杆、梁、板、壳、三维块体、二维平面、管道等各种单元的各种复杂结构的静力分析。

（2）各种复杂结构的动力分析，包括频率、振型和动力响应计算。

（3）整机（如水压机、汽车、发电机、泵、机床）的静、动力分析。

（4）工程结构和机械零部件的弹塑性应力分析及大变形分析。

（5）工程结构和机械零件的热弹性蠕变、粘弹性、粘塑性分析。

（6）大型工程机械轴承油膜计算等。