传统钣金展开放样方法简介

传统钣金构件的展开放样有以下两种方法：图解法、计算法。

1.图解法

图解法是基于画法几何原理，利用几何作图完成全部展开步骤，方法直观，但效率低、误差大、步骤繁杂。常用的图解展开方法一般有以下3种。

●平行线展开法：主要应用于素线相互平行的构件。

●放射线展开法：应用于素线交汇于一点的构件。

●三角线展开法：由可展表面组成的构件一般都可以用三角线展开法绘制展开图。

下面将分别介绍这3种展开方法。

（1）平行线法

平行线法主要适用于棱柱面、圆柱面、椭圆柱面等柱面构件表面沿着与棱线或素线垂直的方向旋转打开，并依次摊开在同一平面上形成展开图。比如，对于斜截面柱面，一般先将圆柱表面分成若干等份，并确定各等分处素线的实长，然后将圆柱底面圆周展为直线，在直线的各相应等分点处画出各素线的实长，显然各素线是相互平行的，用曲线连接各素线上端点，即得到斜截面圆柱的展开面。

当形体表面有平行的边线或棱的构建时，如圆管、矩形管、椭圆管以及由这类管所组成的各种构建，均可用平行线法作展开图。平行线法就是将构建表面分成若干平行部分平面或用素线分成若干梯形小平面进行展开，如图6-82所示。

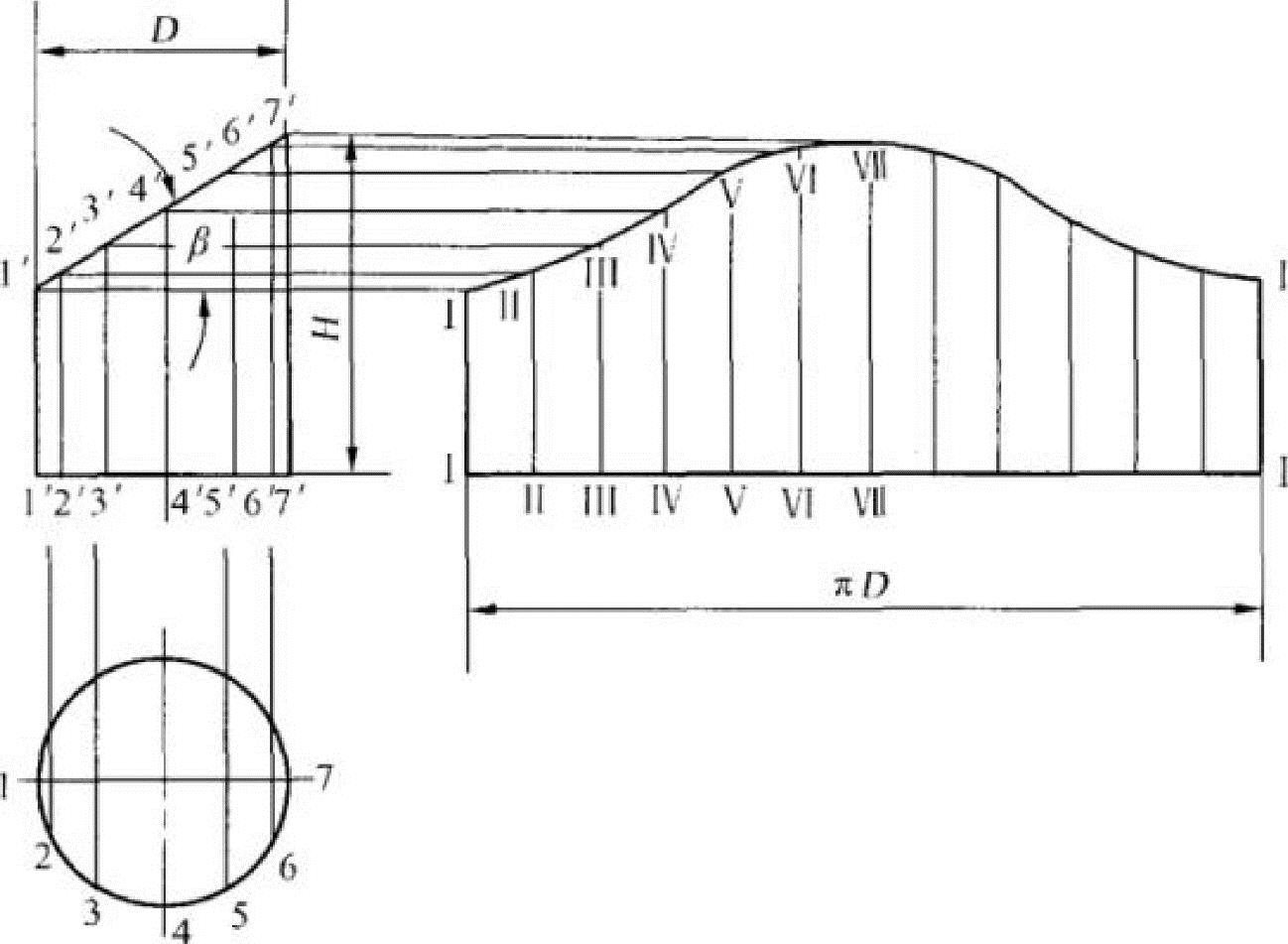
图6-82 平行线法展开斜截圆柱面

平行线法是作展开图的基本方法，应用最为广泛，其主要操作步骤如下。

●画出制件的主视图和断面图。主视图表示制件的高度，断面图表示其周长。

●针对其曲面的结构，依照一定的规则，将该曲面划分为若干个彼此相连的梯形微面元。

●对每个梯形微面元，都用其四顶点组成的平面梯形逐个替代，即用N个梯形替代整个曲面，其替代误差随着N的增加而减小。

●在同一平面上按同样的结构和连接规则组合画出这些梯形，得到模拟曲面的近似展开图形。

（2）放射线法

放射线法主要适用于棱锥面、圆锥面、椭圆锥面等锥面结构的展开。放射线法的绘制原理与平行线法类似，但锥面展开后各素线不是平行面，而是相交于一点。放射线法作图是通过假想沿结构的某条棱线或素线将构件打开，然后将构件表面围绕锥顶打开，在换面逼近时使用的面元是三角形，但这些三角形共一顶点，呈扇状摊开在同一平面上形成展开图，如图6-83和图6-84所示。

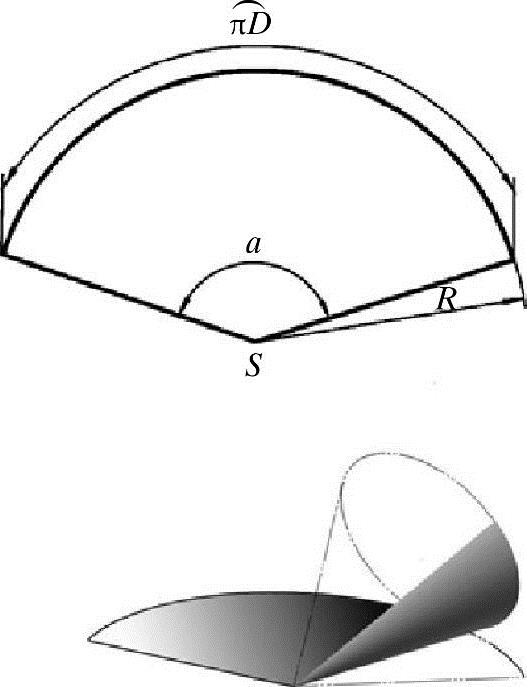
图6-83 侧滚法展开正圆锥

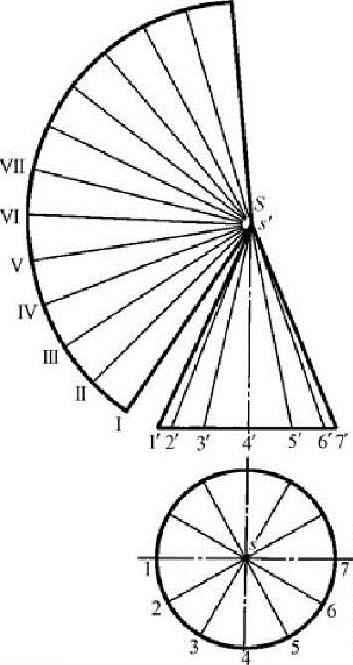
图6-84 正圆锥的展开

放射线法的主要操作步骤如下。

●针对某曲面的结构，依照一定的规则，将该曲面划分为N个共一顶点、彼此相连的三角形微面元。(www.xing528.com)

●对每个三角形微面元，都用其三顶点组成的平面三角形逐个替代，即用N个三角形替代整个曲面，其替代误差随着N的增加而减小。

●在同一平面上按同样的结构和连接规则组合画出这些呈放射状分布的三角形组，从而得到模拟曲面的近似展开图形。

（3）三角线法

三角线法主要适用于盘旋面、不可展的直纹曲面等曲面的近似展开。三角线法的原理是将形体的表面近似地看作由许多边与边相邻的三角形构成，然后求出各个三角形的真实形状，并将它们拼凑在一起。用三角线法展开钣金件时，通常先在曲面上作一系列素线，将曲面划分为若干小曲面单元，每个小单元一般分为四边形曲面，然后利用四边形的一条对角线将四边形分成两个三角形，最后把全部三角形依次拼画在一起形成展开面。

三角形法在换面逼近时使用的面元是三角形，可用于柱面、锥面等各种曲面的展开，应用广，准确度高。图6-85为天圆地方构件的展开。

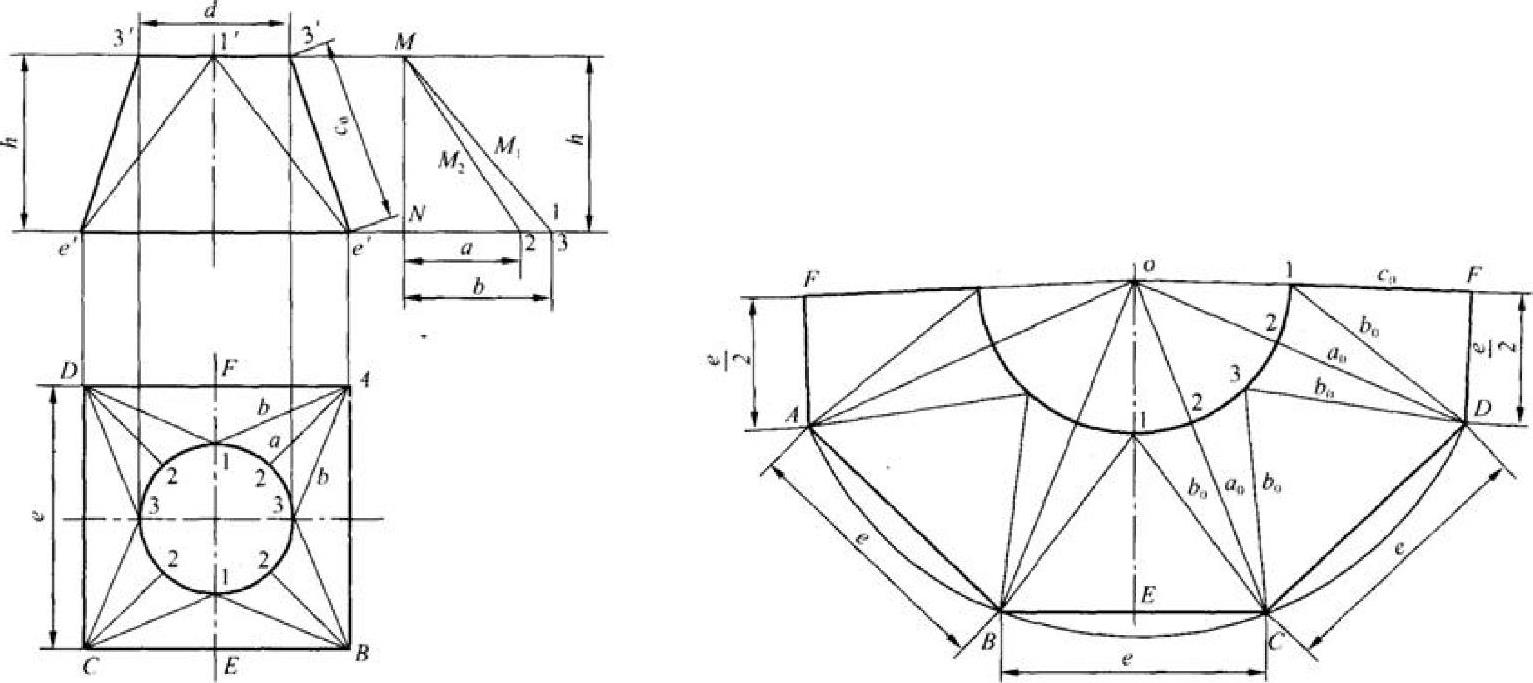
图6-85 天圆地方构件的三角形法展开

三角形法的主要操作步骤如下。

●针对某曲面的结构，依照一定的规则，将该曲面划分为若干个彼此相连的三角微面元。

●对每个三角微面元，都用其三顶点组成的平面三角形予以替代，即用N个三角形替代整个曲面，其替代误差随着N的增加而减小。

●在同一平面上按同样的结构和连接规则组合画出这些三角形，于是得到曲面的近似展开图形。

2.计算法

钣金展开的计算法主要基于解析几何原理，根据构件的已知几何尺寸，通过理论计算推导出形成构件展开图所需要的几何参数，然后通过曲面拟合，绘制出构件的展开图或者把数据传送给数控系统进行加工编程。对于可展开曲面，一般可以直接推导出展开面上边界曲面的方程，但习惯上仍可求出曲面上各等分素线端点的位置坐标，或者素线的长度；对于不可展开面，可计算出近似展开时所需的长度、半径等几何参数。

钣金展开放样的计算法精度高，通用性强，能够克服图解法展开大型构件时场地占用面积大的缺点，还能为计算机辅助展开提供算法基础，所生成的数据能够用于后续的自动化下料设备。常用的计算法有实长计算法、坐标计算法、参数化方法和计算数表达法四种。

实长计算法较多地适用于用三角线图解方法展开的构件。实长计算法在构件展开时通常计算出有关线段的实长，然后再利用这些实长数据来绘制构件的展开图。该方法用计算代替了图解法中求线段实长的作图过程，所得结果更加准确，但最后的展开图一般仍用作图方法来完成。图6-86为圆侧口圆底连接管用实长计算法进行展开时的几何模型，其已知尺寸为D、d、L和H，有关计算公式如下。

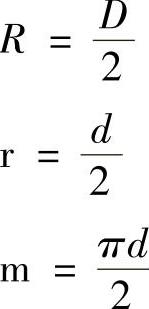
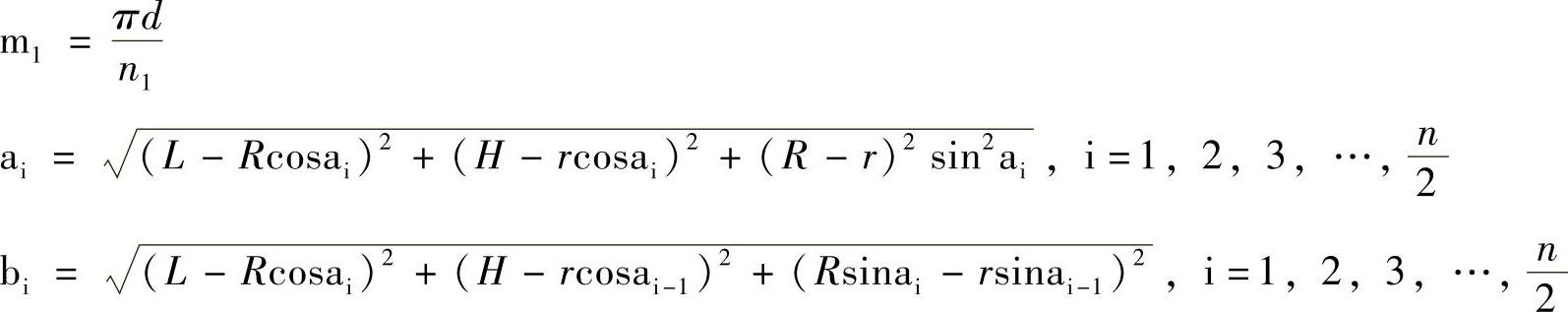
式中，n、n₁分别是求上、下口圆周等分数量，通常取n=n₁；a等分角度的计算增量a_i=i×360°/n。根据求得的线段实长a_i、b_i，即可画出展开图形，其中曲线s₁和曲线s₂可由各线段的端点拟合而成。

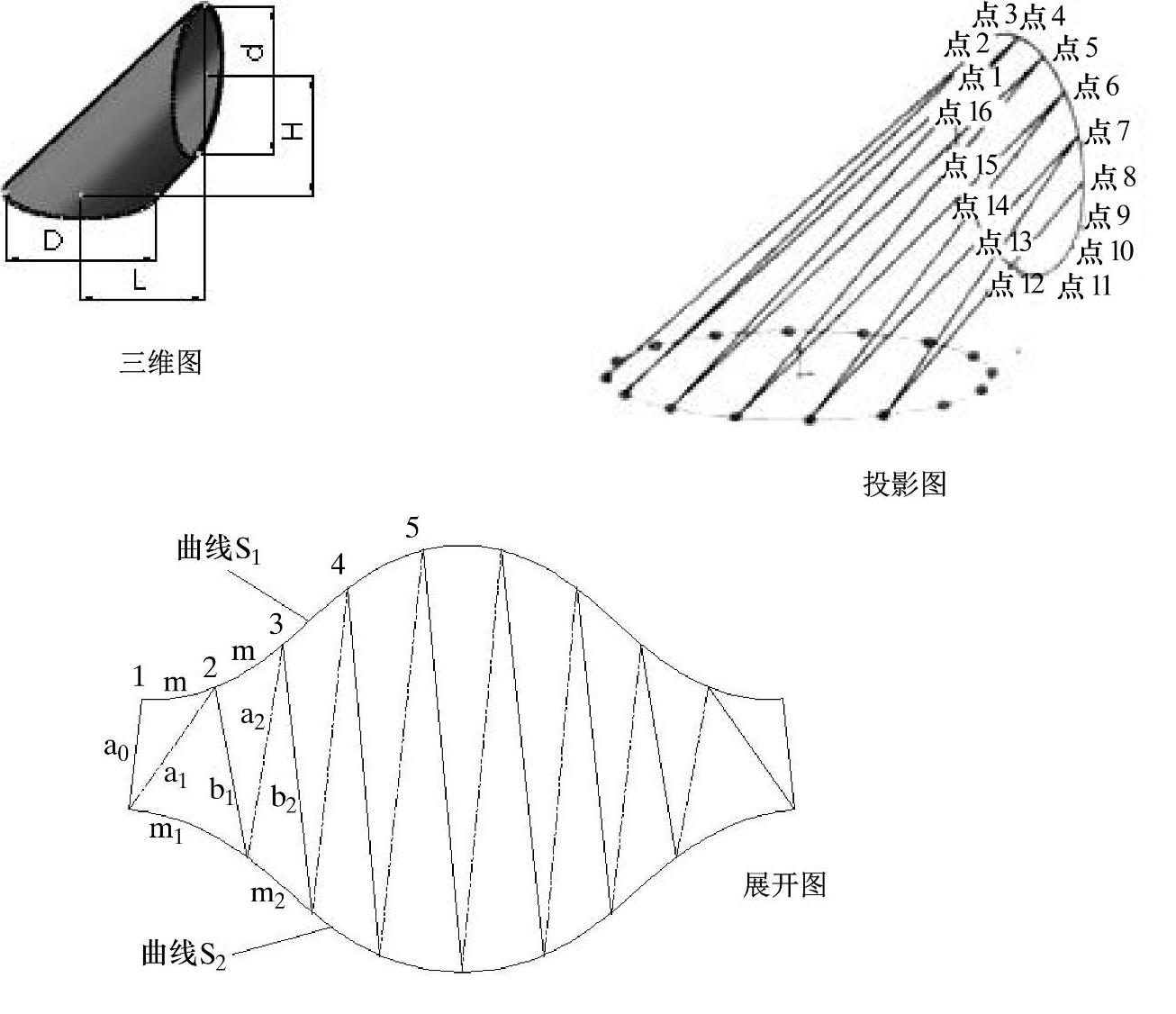
图6-86 计算法

坐标计算法主要适用于可展开曲面，特别是柱面和锥面的计算展开，这类构件在图解法中一般是用平行线法和放射线法展开的。坐标计算法的数学基础与实长计算法没有什么本质区别，用坐标计算法展开构件时，首先把展开图放在一平面直角坐标系或坐标系中，建立构件空间曲线与其展开曲线之间从三维到二维的点的对应关系，然后直接计算出展开图中点的二维坐标。

对于一些常用的钣金结构，通过变化几个几何参数，就可以得到相同种类、不同形状和结构的系类构件，这类构件的展开放样就可以采用参数数化方法，即建立起尽量通用的计算展开数学模型，展开时通过参数赋值的变化实现相同类型、不同尺寸的构件的展开。

对于一些特别常用的典型钣金构件，在推导出展开面的计算公式之后，为了便于使用者查阅，可将计算数据制成图标，该方法即为计算表法。