锚杆方位选择对阻滑力系数的影响

对不稳定岩体的最佳锚固矢量的选取决定于两个因素：一是要便于施工；二是要最大限度地发挥锚固件的作用。对于前者，只要锚固方向的倾角大于5°就可以满足施工方便的要求了；对于后者，要明确不稳定岩体的滑动方向和倾角（表9-12）。

表9-12　边坡不稳定岩体的滑动的方向与倾角及加固方向和倾角表

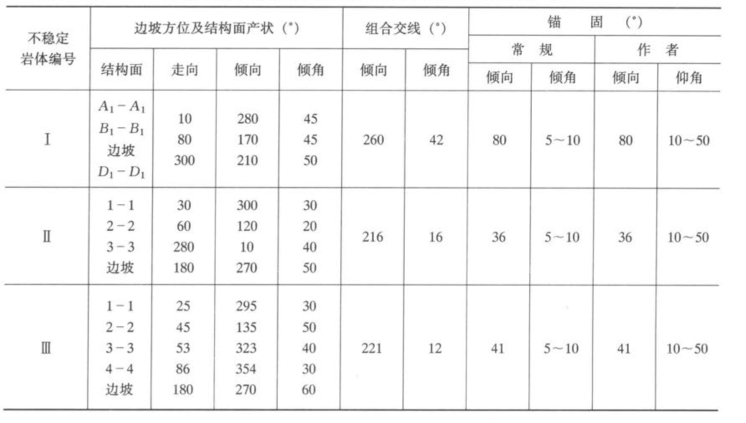
图9-34　边坡锚固示意图

（a）锚固件倾向与组合交线倾向相反；（b）锚固杆件倾向与组合交线倾向相同P—锚固杆体的容许拉断力；N—杆体作用在组合交线上的正应力；β—组合交线的倾角；γ—锚固杆体的倾角；α—边坡坡角

Ⅰ号不稳定岩体加固方向与加固倾角，由图9-34（a）可以看出，用锚杆加固不稳定岩体时，固杆件倾向与不稳定岩体的组合交线倾向相反，可以把锚固为P 分解为正应力N 与阻滑力R2，而N 与组合交线附近的摩擦系数的积R1 构成了阻滑力，两力由式（9-11）可以看出，它们与P、β、γ与tanφ有关：

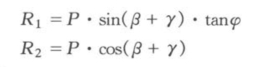
每根杆件所形成的阻滑力：

令sin（β+γ）·tanφ±cos（β+γ）为±Rf，-Rf 为阻滑力系数，Rf 下滑系数。

由图9-34（b）可以看出，用锚杆加固不稳定岩体时，由于杆件加固方向选择失当，不仅不会加固不稳定岩体，而会促使不稳定岩体更加不稳定。其中：

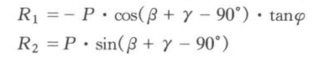
下滑力：(www.xing528.com)

对公式（9-16）、（9-17）的讨论　一般来说，图9-34（a）所示的不稳定岩体的锚杆加固方向和倾角，从根本上分析是对的，然而不一定是最佳的。假定组合交线的倾角为42°，组合交线附近的摩擦角为26.6°，锚固杆件的倾角γ为变数，由30°变化到-30°，利用公式（9-16），可以作出图9-35。将公式（9-16）可以简写成R=-P·Rf。其中P为锚固杆体的容许拉断力，-Rf 为阻滑力系数。由图9-35可以看出，-Rf 当γ为30°时仅等于0.784，而当γ为-15°时，-Rf 可以大到1.118。由此可以看出，若选用γ为-15°时，比选用30°时，可以提高锚固件的阻滑力42.6%。

图9-35　锚固件杆体的阻力系数

Rf 与锚固角γ的关系曲线图
γ—倾角为正值，俯角为负值

常规选用的γ角分别有5°、10°、15°、20°等4种，若按著者推荐的γ为-15°，可以分别提高锚固件的阻滑力7%、10%、15%和23%。

由图9-34（b）所示原理推导出的公式（9-12），是著者提醒有关人员，不要一味迁就施工条件的方便，而最佳加固效果才是我们要追求的。如果组合交线的倾角β=42°，γ=70°tanφ=0.5，则按9-12公式可以算出-Rf 仅有0.088；如γ=15°按公式（9-16）计算的-Rf =1.118，后者是前者的12.7倍。由此可见锚固杆件的方位选择是多么的重要。

根据9-34（a）所示原理，我们推导出了锚固杆件在不同的γ与β角的情况下的不同阻滑系数公式（9-16），并绘制了图9-35，由该图可以清楚地看出：

（1）无论锚固件的倾角γ怎么变化，它们的阻滑系数-Rf 随着组合交线倾角β值的变大而绝对值变小；

（2）采用低倾角的锚固件（图9-36），其阻滑力要比高倾角锚固件的阻滑力要明显的大。

图9-36　锚固杆件的阻滑系数Rf 与组合交线的倾角β的关系曲线

【注释】

[1]kg是质量单位，kgf（千克力）才是力的单位，但此力的单位属已废除的计量单位，1kgf=9.80665kN——编辑注。