用极射赤平投影法解决岩体加固方向与倾角问题

运用赤平极射投影方法求解不稳定岩体的加固方向与倾角，是以赤平极射投影的基本原理和静力学的基本原理为依据的。该方法假定所有的地质结构面都是平面；假定所有的地质结构面贯穿整个研究的岩体；假定岩块是刚性的，块体本身没有变形和破坏；假定地质结构面数目是有限的；整个被分析的岩体处于三维笛卡儿坐标系统之中，y 轴指向正北，x 轴指向正东，z 轴指向上方。

关于刚体的概念，在边坡、坝基、洞体等稳定性分析中，岩体受力后，本身形态是可能有变化的。如岩体中的断层破碎带，在外部载荷作用下，出现压缩变形；露天矿开挖卸荷条件下会出现岩体回弹变形。在一般的情况下，当岩体受力后形状的改变与原来的整个岩体相比，是微小的条件下，在静力学及理论力学中研究岩体的平衡时，可以将这种形状的改变，忽略不计，使得理论分析更为理想，而所发生的误差也不会太大。因此，可以把岩体看做刚体。

作用于岩体上的力，一般以力的3要素来表示：①力的作用点；②力的方位和指向；③力的大小。根据力的3要素，力作用于岩体上，必须有着力点，实际上当然不可能集中在一点作用，而必须有块相当的面积或体积来分布它的作用，因此，力都是“分布力”。在岩体稳定性分析中，为了简化起见，都以集中力表示。

作用在岩体上的力，不只是一个，而是许多时，这许多力合称为力系。在岩体稳定性分析时，根据力系内许多力作用的情况不同，将力系分为：平面力系和空间力系。

作用在岩体上的许多力，如工程荷载、地震力、构造应力、爆破力以及岩体自重等等。如果它们的作用线不在同一平面内，这就是空间力系。事实上岩体都是立体的，作用在它上面的许多力，一般不在同一平面内，所以，大多数的岩体工程，如边坡、地下洞室、大坝基础等等，都是处在空间力系的受力状态中。

为了更好地研究不稳定岩体的加固方向和倾角，著者在此节内大量引用了孙玉科教授介绍的赤平极射投影方法以及他所创造的“实体比例投影”［18］，正由于在这些创造性研究成果的基础上，著者才能可能研究解决岩体的加固方向与倾角问题。现将我们的研究成果介绍于后。

（一）赤平极射投影的基本原理

赤平极射投影是表示物体上的点、线、面的角距关系的平面投影，并不涉及面的大小、线段绝对长度或点与点间的绝对距离。

投影原理：赤平极射投影是利用一个球体作为投影工具，如图9-13。通过球心作一平面“NWSE”叫赤平面，极射就是从球体的一个端点F（称为极点）发出的射线，如FS，FH，等。H 是球体上的一个质点，由极点F 向H 发出的射线“FH”，必然通过赤平面NWSE，射线与赤平面的交点M，就叫做质点H 在赤平面上的投影。如已知结构面（HNKS）的产状：走向SN，倾向E，倾角α，求它的赤平极射投影：

（1）赤平面上的E，S，W，N 分别代表东、南、西、北的方位，如图9-13 所示。作通过球心，并走向南北的面，同时倾向东，这个面在球面上的位置为HNKS，即结构面与球面的交线。HNKS 面在球体中与赤平面的夹角α，就是它的倾角。

（2）结构面与上半球面的交线是由极点F 向发出射线，与赤平面的交点可连接成这个弧线就表示结构面在赤平面上的投影曲线，即求得的结构面的赤平极射投影。

图9-13　结构投影原理示意图

图9-14　结构面投影图

（3）把赤平面从球体中拿出来，如图9-14，弧线即结构面的投影线，SN 表示走向方位，弧凹所指的方位向东，是倾向，W与M之间的距离表示倾角α，当倾角等于90°时，M点落在球心上，则W与M的间距最大，等于球的半径；当倾角等于零度时，M点与W相重合，无间距。作图时利用投影网上的刻度，可以直接读数，如图9-15（a）。

图9-15　力线投影图

作图时一般选用20cm或10cm为直径的吴氏投影网为适宜，投影网上的上下两极分别代表南北，左右两侧代表东西。作图时把绘图透明纸放在投影网上，用圆规按投影网相同的半径画圆，在圆周上标注东、南、西、北的4 个方位。然后根据结构面的产状，运用投影网就可以绘出投影图，即文献上所说的上半球极射投影图。

（二）空间力系的基本投影方法

1.力线投影

用线段的长短和方位代表力的矢量。在选定比例尺之后，线段长短表示力的大小，线段的倾向和倾角表示力的方位。面的产状用其倾向和倾角表示。

如已知力P 作用在水平面上，力P 的产状：指向210°，俯角40°。绘出力P 的投影。

作图步骤：

（1）先在透明纸上画好投影圆，其半径与投影网半径相等，并在投影圆上标注方位：东南西北。然后将透明纸覆盖于投影图上，使南北的方位与投影网的南北极重合。重合后确定力P 的指向方位210°，标记A 点，如图9-15（a）。

（2）在投影网上，使A 点与投影网的赤道线一端相重合，如图9-15（b）。然后根据力P 的俯角40°，确定B 点。BO 连线即表示力P 的投影。

（3）将透明纸脱离投影网，得到力P 的投影，如图9-15（c）。BO 向圆心的方位表示指向（210°），CB 线段表示倾角40°。

（4）根据图9-15（c），沿力P 的指向方位作一剖面，则得到力P 作用线的剖面图，当选定比例尺时，力线的长度即表示力P矢量的大小，如图9-15（d）所示。

2.力面投影

力面有两个含义：一是指力所作用的平面，一般是作用在节理面上、层面上、断裂面上等等。在岩体稳定分析中这些面统称为结构面。二是指力所在的平面，如图9-15（d）所示，在空间力系分析中需要求作包括力的平面。这两种力面在投影中表示是一样的，都需要给出它们的产状才能绘制投影。

已知力面的产状，走向北30°东，倾向南东，倾角30°，绘作投影。

在图9-16（a）上，采用上述方法，画出力面的AB 走向线；在图9-16（b）上，画出力面的弧线将透明纸脱离投影网后，即得图9-16（c），其AB连线为力面走向，凹形向着圆心的方向为其倾向，从C点到D点的距离为倾角。

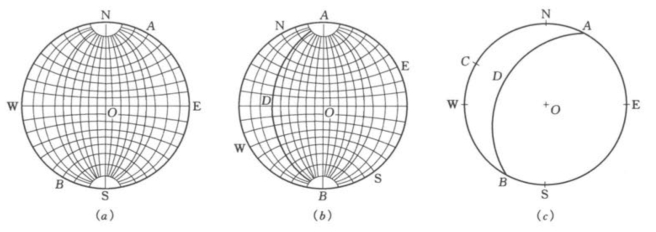
图9-16　力面投影图

3.力面法向线投影

在岩体力学分析中，经常需要知道受力的结构面上所受法向（垂直于结构面的方向）应力的大小，如已知力面的产状，走向N50°W，倾向40°，倾角40°。求力面的法向线投影。

首先画出力面的投影，如图9-17（a）；其次是根据法线垂直力面，因而法线的投影也垂直于力面的走向线ab 的道理，将法线CO 投影在赤道线上，如图9-17（b），C点与O点的连线CO即为法向投影；最后判读9-17（c），可知法线倾向为220°，倾角为50°。

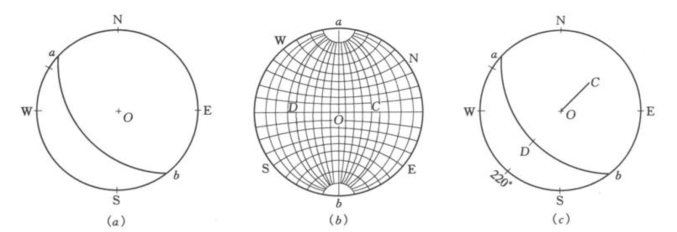
图9-17　力面法向线投影图

4.含力线面投影

通过已知力线，可以作无数个面。若作一个特定的面，必须给定面的走向。

已知力线的产状，指向北40°东，俯角36°。作通过力线，并走向北20°西的面。力线的投影为CO；画NW340°面的走向线ab；使ab线与北南极重合，根据C点所在的经线划弧，即得含力线面的投影acb；判读图9-18，可知该面的倾角为40°。

5.力面的垂直投影

作已知力面的垂面，如果不给定垂面的走向线，可作无数个垂面。因此必须给定垂面的走向方位，才能作出它的投影。

如已知力面的产状，走向N50°W，倾向40°，倾角40°。求作已知力面的垂面，垂面的走向为N20°W。

已知力面的投影垂面走向线cd；画已知力面的法线投影oe（法线垂直力面）；使c，d两点与两极点重合，根据c点所落的经线位画弧得该弧即所求已知力面的垂直投影（图9-19）。

6.通过两个力线的共面投影

三维空间力系的合成与分解，首先应求出两个空间力的共面，求出共面之后才能进行力的合成与分解。

如已知两个力线：力P 的指向30°（方位角），俯角40°；力N 指向140°（方位角），俯角30°。求通过力P 和力N 的共面投影。

作ao 与bo 分别代表P 和N 的投影；使a、b 两点同时落在同一条经线上，画弧该弧即为共面投影，其走向为NW345°，倾向70°，倾角为50°（图9-20）。

7.两力面的组合交线

图9-18　含力线面的投影

图9-19　力面的垂直投影

图9-20　含两力线的共面投影

已知：力面的走向为NE40°，倾向为SE∠30°，力面的走向NW340°，倾向为NE∠40°，作两个力面的投影两力面的交点为c，连cO 即为两个力面的组合交线；交线倾向SE117°，倾角为30°（图9-21）。

8.垂直于力线面的投影

如已知力线的产状：指向北30°东，俯角40°，求作垂直于该力线的面。

根据力线产状，作其投影AO，使AO 与赤道线重合，从A 点起向圆心方向查90°定点，通过B点按投影网画弧即为垂直力线面的投影。的倾向210°，倾角50°（图9-22）。

9.同时垂直两个力面的共面投影

如已知两个力面的产状：一是倾向SW200°∠40°；一是倾向NE70°∠50°。

作两个力面的投影分别作两个力面的法线投影；力面的法线投影）和BO力面的法线投影）；通过A、B 点画弧即为同时垂直两个力面的共面投影。共面倾向NW320°，倾角66°（图9-23）。

图9-21　两力面组合交线投影图

图9-22　垂直力线的投影图

图9-23　垂直两个力面的共面投影

10.求两个已知力面的夹角

如已知两个力面的产状：一是SE130°∠50°；二是NE10°∠40°。

绘出两力面的投影得知组合交线AO；作出交线AO 的垂面投影两个交线，OA 与OB；CO 和BO 之间的夹角为∠BOC。该夹角为105°（图9-24）。

（三）求空间共点力系的合成

岩体稳定分析是一个空间力学问题。岩体的稳定取决于空间力系的平衡条件。为解决这一问题，首先要研究力系的合成与分解。解决三维空间力系问题，应用解析法比较复杂，但应用赤平极射投影法比较简单。在这里应用赤平极射投影法，主要是解决空间共点力系的关系，即力的作用线不在同一平面上，但有共同的交点，作图时把这个共点设在投影圆的中心。

1.两个空间共点力的合力

已知力P1 为80kgf，倾向SW210°，俯角40°；力P2 为60kgf，倾向SE140°，俯角50°。

（1）AO 为P1 的投影，BO 为P2 的投影（图9-24）。

（2）绘作P1 与P2 的共面投影

（3）在共面内用角数据表达P1 和P 2 的相对位置，为此将图9-24 覆于投影网上，使共面的走向线KH 与投影网的两极点重合，然后，根据A、B 两点所落的纬线，来判读它们的角数据。

（4）按比例尺绘共面矢量图解即将图9-25（a）中的投影面KBAH，转换为图9-25的真实面先根据P1 和P2 的相对位置，绘出力线的方位A 与B，如图9-25。

图9-24　求解两个已知力面的夹角图解图

图9-25　共点力系合面图解

然后，再选定比例尺，以1cm 长线段代表20kgf 作图，按平行四边形法则，进行图解。

得合力：

根据9-25，可知R 的相对位置：

（5）根据R的相对位置，求真实的空间方位。即在共面投影线上，按∠HOM=74°，在图9-25中确定M点，MO为合力R的投影，如图9-25所示。根据R的投影可判读倾向是186°，俯角为50°。

作图结果：合力R 等于128kgf，空间方位：指向186°，俯角50°。

2.3个空间共点力系的合力

力P1 为100kgf，倾向30°（方位角），俯50°；

力P2 为60kgf，倾向130°，俯角40°；

力P3 为40kgf，倾向270°，俯角20°。

（1）作力线的投影，分别为AO，BO，CO，如图9-26（a）。

图9-26　三个空间共力点系合面图解

（2）先绘作P1 和P2 的共面投影

（3）根据9-26（a），判读P1 和P2 在共面投影线上的相对位置，以角数据表示如下：

P1的角数据，即∠KOB=50°，P2的角数据，即∠KOA=116°。

（4）按比例尺绘P1和P2的共面矢量图解，将共面从投影圆中取出来，得到图9-26（b），图中P1和P2的相对位置，是根据它们的角数据绘制的，选力线的比例尺，1cm为20kgf，按平行四边形法则，图解求得R1 的大小：

又根据图9-26（b），可判读R1 在共面上的相对位置，角数据∠KOG=92°。

（5）将合力R1，在共面上的相对位置，转换到投影图中，求在共面投影线上的相对位置，根据角数据∠KOG=92°，可在投影线上定出R1力线的投影GO，如图9-26（a）所示。

（6）绘R1和P3的共面投影线并判读R1和P3在上的相对位置：

R1 的角数据　∠FOG=60°。

P3 的角数据　∠FOG=160°。

（7）按比例尺绘R1 和P3 的共面矢量图解，如图9-26（c），根据平行四边形法则求得合力R 的大小：

则

根据图9-26（c），可判读R 的角数据∠FOQ=77°。

（8）根据R 在共面上的相对位置，把它转换到共面投影线上去，得到力线R的投影是QO。同时又可判读R 的倾向是45°，倾角是72°。

作图结果：R=135kgf，倾向45°，俯角72°。

小结：

可以把上述两例的图解步骤，归纳为：

根据已知力的产状条件，作力线的投影；利用两个力线的投影，求两个力的共面；在共面投影上判读各力线的相对位置，以角数据表示；按比例绘制共面上的力矢量图，运用平行四边形法则求合力的大小及判读它的相对角数据；将共面矢量图上的合力相对角数据，转换在共面投影上，确定合力的空间方位。

（四）空间共点力系的分解

在岩体稳定分析中，先是求合力，而后根据岩体结构条件，将合力再进行分解，求得结构面上所受分力的情况。

1.一个合力分解为两个分力

如已知合力及求R 力作用结构面上的法向分力和滑动结构面上的下滑分力。合力R为50kgf，其倾向140°，倾角40°；结构面走向30°，倾向300°，倾角30°。

图9-27　一个合力分解为两个分力图

（1）绘作合力R 的投影FO 和结构面的投影如图9-27（a）。

（2）画结构面的法向线投影QO［如图9-27（b）］。画法向线与合力R 的共面投影

（3）法向力方向即法向线投影方向QO；沿结构面下滑分力的方向即是共面与结构面组合交线EO 的方向。

（4）确定共面内合力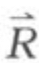，法向力，下滑力的相对位置：

（5）根据在共面内的相对位置按比例绘制力的矢量图［图8-27（c）］，根据平行四边形法则将分解为和(www.xing528.com)

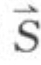得=46kgf；=20kgf，在这里要特别注意的方向。根据图9-27（c）所示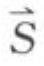，不是下滑分力，而是上滑分力；垂直于结构面。

如果还需要判读和的空间方位，可根据图9-27（b）。按和箭头指向方向延长至大圆周上，可直接读出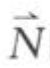的倾向118°，倾角68°；的倾向167°，倾角20°。

2.合力分解为三个分力

如已知合力为100kgf，求分解为垂直于3个结构面上的分力它们的已知条件如表9-4 所示。

（1）如图9-28（a），合力的投影是AO，结构面的投影是

（2）3个分力分别垂直于3 个结构面，因此它们的方位，即是相应的结构面法向方位，在图9-28（b）中绘制法向线投影，同时还可以判读法向线的方位，如表9-5 所示：

表9-4　已知条件表

表9-5　各结构面的法线方向表

（3）先绘P1O 与P2O 的共面投影再绘P3O 与R 的共面投影如图9-28（b）中所示。

（4）绘'的组合交线BO，BO 为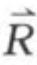的第一次分力 投影。

（5）在共面作第一次分解：一个是P3O；另一个是

即：

在共面的相对位置：

的角数据：∠bOA = 91°

（6）根据上的相对位置，绘力的矢量图，如图9-28（c）。选定比例尺，并按平行四边形法则，求得：

图9-28　合力图解为三个分力图

（7）因BO 是的组合交线，所以BO 也在共面内，这样在内有三个力：

在共面 的相对位置：

的角数据：∠a'OB = 56°

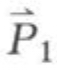的角数据：∠a'OP1 = 112°

的角数据：∠aOP2 = 55°

（8）根据在共面上的相对位置，绘力的矢量图，如图9-28（d），按平行四边形法则，求得：

图解结果如表9-6。

表9-6　图解成果表

（五）实体比例投影

运用赤平极射投影方法可求结构面在岩体中的空间方位，但不能表示结构面的具体位置及不稳定岩体的形状和大小。若用实体比例投影方法与其结合起来，就可以进行岩体稳定分析中的岩体重量计算。

实体比例投影，是用垂直投影方法将岩体的立体结构化为平面结构，并根据实测数据按比例绘出不稳定岩体的断面图。

如图9-29 所示，边坡被两个结构面切割的不稳定体为KMLZ，它将沿结构面组合交线MZ的方向向下滑动。

1.投影方法

将不稳定体KMLZ 垂直投影到水平投影面上，得到K'M'L'Z'，其中MZ为两个结构面的组合交线，它的投影为M'Z'。LZ及KZ 为两个结构面分别与边坡坡面的交线，它们的投影为L'Z'及K'Z'。KM 及LM为两个结构面分别与边坡坡顶的交线，它们的投影为K'M'及L'M'，这些交线即为不稳定体的边界条件图（图9-29）。

立体示意图中K及L两点为两结构面的实测点，两点间的距离在水平投影面上为K'L'，是实测的比例长度。平面投影图的比例是根据实测边坡或设计边坡的断面底宽E 适当地选取，以便精确表示方位，又便于绘制图形。比例尺可选用1/100、1/200、1/500或1/10000 等等。

2.作图步骤

边坡的方位，实测结构面的产状及实测点为已知条件，如表9-7所示。求边坡变形的边界条件。

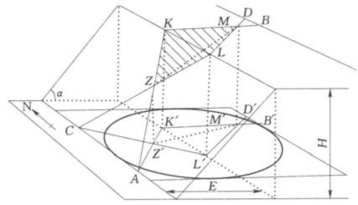
图9-29　实体比例投影立体示意图

表9-7　边坡方位及结构面的产状

表9-9　实体投影方向与赤平投影方向的关系

表9-8　按赤平极射投影求出的交线方位

（1）采用赤平极射投影方法求结构的组合交线。根据边坡的方位和结构面的产状要素，应用吴氏投影网，绘制投影曲线，分别为D1-D1、A1-A1、B1-B1，如图9-30（a）所示。在3 条曲线上有3 个交点K1N1M1，做各点向圆心O 点的联线，分别得出结构面的组合交线方位。K1O 和N1O 为两结构面分别与边坡坡面的交线，M1O 为两结构面的组合交线，其方位如表9-8 所示。

图9-30　图解分析示意图

（a）赤平极射投影面；（b）实体比例股影图；（c）边坡断面图

（2）根据实测边坡断面底宽E，选取适当的比例尺，以E 为半径画圆，作实体水平投影图，如图9-30（b）所示。其次将投影面分为左右两侧，以通过圆心的直线为界，左侧为坡面交线的投影面，右侧为坡顶面交线的投影图。

（3）根据两结构面的实测距离及相对位置，按比例画在投影面上，即为K2 及N2 的两点。

（4）以K2 及N2 两点为基础，引组合交线的方位。以赤平投影求得的方位为准。按方位角度，实体投影方位等于赤平投影方位。按作图方法，实体投影方位平行于赤平投影方位，如表9-9 所示。

作图后，得出边坡的不稳定体为K2O2N2M2。

（5）根据水平投影图，引作边坡断面图。如图9-30（c），断面图应通过M2O2 的方向。断面图上的M3及O3 两点为投影平面上的M2 及O2 两点的投影。两点的联线M3O3 为边坡不稳定体的滑动线，该线与水平面的夹角为β，与边坡坡面的夹角为φ。角数据的大小可直接从边坡断面图上测出。所测得的数值即为边坡计算的边界依据。

（六）由3 组或4 组结构面构成的边坡滑动面的图解分析

3组或4组结构面所形成的非稳定组合结构，其性质仍然取决于各结构面的组合交点在投影面上的位置。若组合交点之一，位于坡面投影半圆的范围之内，即形成非稳定结构。

现设想两个实例：一是由3个结构面组合的边坡；另一是由4 个结构面组合的边坡，它们的边坡方位及结构面产状如表9-10所示。

按着表9-10的方位和产状，分别绘制赤平极射投影及实体比例投影图，如图9-31和图9-32所示。从实体比例投影图中可以明显地看到，边坡被3个结构面切割的最大的不稳定体为aZcM，被4个结构面切割的最大的不稳定体为aZdM。而其他的不稳定体被各自的最大的不稳定体所包容，为局部的不稳定体。根据上述实例，并通过图解分析，可帮助解决以下几个方面的问题：

（1）通过图解可反映出主要起控制作用的结构面（如图9-31中的1-1、2-2；图9-32中的1-1、2-2）和次要结构面（如图9-31中的3-3；图9-32中的3-3、4-4）之间的关系。

（2）通过图解分析，可明显地反映出边坡的滑动方向，即符合结构面组合交线的方向。

（3）通过图解分析，可反映出边坡变形的形状及规模。

表9-10　边坡方位及结构面的产状

（七）应用空间共点力系的分解法验算岩体的稳定性

有一个岩质边坡，坡高20m，在边坡上有一个滑动体，是由两个结构面组合而成的，如图9-31（a）中的1为透视图；2 平面实体比例投影图；3 沿组合交线Oc 的断面图，已知条件如表9-11。

表9-11　已知结构面及边坡产状表

滑动体的稳定性以稳定系数K 来表示，即抗滑力与滑动力之比。为算出这个系数，首先需要计算滑动体的自重，然后将自重分解为3个分力：一个下滑力和两个垂直结构面的法向力。

图9-31　图解分析示意图

（a）赤平极射投影图；（b）实体比例投影图

图9-32　图解分析示意图

（a）赤平极射投影图；（b）实体比例投影图

（1）首先需要计算滑动体的体积和自重。滑动体为三角形棱锥体acbo（9-33a）

式中　S △——三角形面积△acb；

H ——边坡的高度20cm。

滑动体自重

岩块容重γ=2.5 tf/m3

（2）运用投影方法求滑动面的面积△cbO 和△caO，因两个结构面是对称的，所以两个面的面积相等。

根据已知条件，绘结构面投影边坡面如图9-33（c）。

利用图9-33（c）求滑动面△cbO 各边的角数据关系，根据∠2Oc=42°，∠2Ob=82°和Oc=40m［由图9-33（a）断面图求得］可绘出△cbO，如图9-33（d）所示。

（3）将滑动体自重R 分解为3个分力：两个法向分力N1 与N2，然后绘包括N1 和N2 的共面再绘自重力R 与下滑力P 的共面投影b-b'。

先在共面b-b'上将R 分解为P 和N 两个分力。根据R，P，N 在共面b-b'上的相对角数据，绘矢量图，如图9-32（e），按平行四边形法则求得分力P 和N 的大小得：

在共面上将N 分解为N1 和N2 两个分力。根据N，N1，N2 在共面上的相对位置、绘矢量图，如图9-33（g），按平行四边形法则求：

得

（4）验算滑动体的稳定系数。抗滑力（T）的大小取决于滑动面的摩擦角和内聚力，法向力及滑动面的面积。滑动力为P

抗滑力

稳定系数

这个实例是一个典型例子，主要是为了说明运用投影图解法验算滑动体的稳定性，把这个典型例子弄明白了，掌握了基本方法，碰到复杂的问题，也是不难解决的。

（八）不稳定岩体的加固方向与倾角

目前，边坡与地下洞室岩体加固的勘察设计，大都是工程地质人员在边坡上，在沿地下洞室方向与其垂直方向的勘探平洞里，对出露的地质构造进行工程地质编录的基础上，根据有关规程、规范进行设计。对于一些大型工程，有些单位在编录的基础上，进行一些岩体稳定性的有限元分析、块体分析和地质力学模型试验，而后对不稳定块体进行加固设计。至于加固方向，如何加固，是系统锚固还是随机锚固等问题，就研究甚少，甚至对加固方向从来没有专家进行过研究。

著者在本章里对现行加固勘察设计的方法进行了简要的叙述，其目的在于在研究现状的基础上，提出用极射赤平投影法求解不稳定岩体加固方向和倾角这一极为重要的新方法。

1.对岩体进行岩性构造工程地质编录

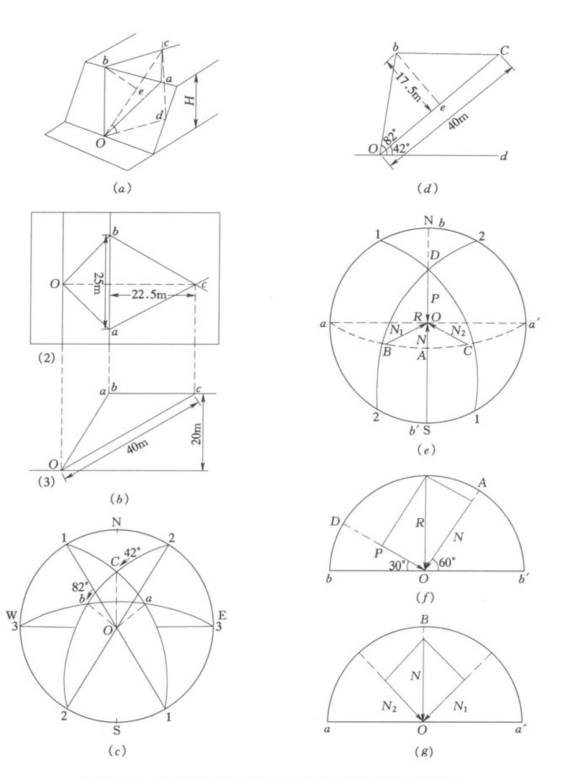
图9-33　应用空间共点力系分解法验算岩体稳定性图

这里所述的岩体是指可能加固的边坡岩体与可能加固的地下洞室岩体。首先对其分布的岩性要有正确的定名，最好用岩矿薄片鉴定，对其厚度、岩相变化和风化卸荷程度等都要论述，尤其对软弱结构面（前已详细介绍）对其空间分布及其规模尺寸要特别予以详细描述；其次对褶皱构造，特别是断层及其影响带，除常规描述项目都要描述外，对其空间分布的产状变化，水文地质、工程地质特性，如含泥情况、透水透浆性以及岩体强度变化都要详细描述；最后，对岩体内的节理裂隙（主要是裂隙）除按常规描述项目进行描述外，要对裂隙宽度最好用塞尺仔细丈量，对裂隙走向长度、倾向长度，要尽可能多地收集资料，要特别注意裂隙分布规模与岩性的关系。

2.在工程地质水文地质编录图上圈出可能不稳定岩体

可能不稳定岩体在某些文献上也有称“关键块体”的。首先在编录图上根据断层交会角锥体（在开挖面上构成的三角体）圈出可能不稳定岩体。

3.对可能不稳定岩体进行稳定性初判

（1）几何判定法。由块体理论可知，块体可动的充分必要条件是：

式中由半空间裂隙（断层）面子集所确定的集合，简称为裂隙锥JP。这个裂隙锥必须是“非空集”，即不是不可能事件。

开挖的半空间集称为开挖锥EP。开挖集与裂隙锥的并集应是空集，即EP 与JP 同时出现是不可能的。再明确地说：若裂隙锥JP 完全包括在空间锥EP 内，则该裂隙锥在几何形态上就可以判属为可动块体。

（2）图解分析法。是用赤平极射投影与实体比例投影两种方法进行图解分析。

1）稳定结构。是指两种结构面的组合交线倾向与边坡倾向相反，或者说，在赤平投影图上两组结构面投影的交点M 位于坡面投影的对侧半圆之内。在实体比例投影图上更为明显，组合交线的M 点落在坡面投影面上，在坡面投影面上无交点，故组合交线向坡内倾斜，一般应属稳定结构。

2）非稳定结构。岩体结构体的稳定与否，取决于各结构面的组合交点在投影面上的位置。若组合交点之一位于坡面投影半圆的范围之内，即形成非稳定结构。

（3）软弱结构面产状及其交线分析法。即利用赤平极射投影方法求解的各组合交线产状及软弱结构面倾向进行岩体稳定性分析。

1）洞室顶拱岩体稳定性分析。在编录图上，凡是见到3个结构面围成的三角形岩体，且各软弱结构面的倾向不能交会者（即角锥体的角锥朝上）为非稳定结构岩体。

2）边坡与洞室岩壁岩体稳定性分析。在编录图上，凡是见到由3 个软弱结构面围成的任意三角形（出露三角形），且3条组合交线倾向临空面的方向者为非稳定岩体，而它们的组合交线倾向临空面的倾角愈大，其稳定性愈差，反之则稳定性就愈大。

4.对初判的不稳定岩体进行力学分析法

对初判的不稳定岩体进行力学分析应有一定的步骤：

（1）在地质编录的基础上，认真分析影响边坡稳定性的工程地质因素。既要从地质成因方面研究岩体变形的发生、发展规律，又要从力学方面研究岩体稳定性的平衡条件和它可能的演变。

（2）研究可能不稳定岩体的边界条件。因为它们的破坏特征，主要受结构面所控制，而岩体结构面的物理力学性质与其有密切关系。

（3）从初判的不稳定岩体的阻力与滑动力等方面进行量的分析计算，只有如此才能判断它们的不稳定程度，补充多少阻力才能使其稳定。解决这个问题已有许多计算公式可供选择，但这并不是惟一的重要问题，而是力学指标的选取，则是具有决定性的问题。

（4）计算可能不稳定岩体的不稳定程度固然重要，而如何决定锚固（加固）方向则是更重要的问题。因为任何不稳定岩体都有其固有的滑动方向，不从最有效或最大限度地发挥锚固件的锚固力进行的设计，都不是好设计。