神经元模型简介

关于人工神经网络，一种广泛认可的定义是“神经网络是由具有适应性的简单单元组成的广泛并行互联的网络，它的组织能够模拟生物神经系统对真实世界物体所做出的交互反应”(Kohonen，1988)。其中的“简单单元”，即人工神经元(以下简称神经元)模型，是构成人工神经网络(以下简称神经网络)的基本单元，是对生物神经元的一种形式化描述。神经元对生物神经元的信息处理过程进行抽象，并用数学语言语义描述，常称为节点或处理单元。

在众多的神经元模型中，提出最早且影响最大的是1943年心理学家McCulloch和数学家W.Pitts提出的M-P模型，如图4-1所示，可以看出，M-P模型是一个按照生物神经元的结构和工作原理构造出来的一个抽象和简化了的模型。M-P模型中，一个神经元同时接收到来自n个其它神经元传递过来的输入信号，这些输入信号通过带权重的连接进行传递，神经元接收到的总输入值将与神经元的阈值进行比较，然后通过激活函数处理，以产生神经元的输出。

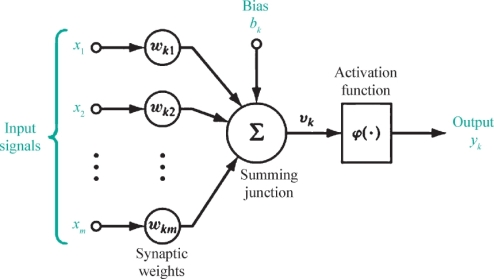
图4-1　M-P神经元模型(www.xing528.com)

M-P神经元模型中，激活函数反映了神经元输出与其激活状态之间的关系，不同的激活函数使得神经元具有不同的信息处理特性。常用的激活函数有4种形式，分别为:阈值型、非线性型(S型，如Sigmoid函数)、分段线性型(如ReLU函数)、概率型。图4-2给出几种典型的激活函数。把许多个神经元按照一定的规则连接起来，就构成了神经网络。M-P模型开启了人工神经网络的序幕。

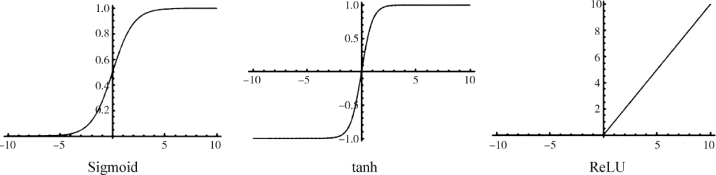
图4-2　典型的激活函数