基于空间关系的遥感图像检索技术

随着对地观测技术的发展，可获取的遥感图像的空间分辨率越来越高，在光谱特征、纹理特征、形状特征等视觉特征的基础上，增加目标之间空间关系特征的表达和空间推理，可以有效提高遥感图像的分类、识别和检索的精度。如图3-15所示，图中红色区域中包含的多个目标(建筑物)之间存在明显的空间关系，当检索类似的由一组目标构成的复杂场景(如机场、码头、停车场等)时，必须考虑多个目标之间的空间关系。但是，目标之间的空间关系对计算机来说是一个复杂而模糊的概念，除了需要研究图像上目标之间空间关系的描述模型，还要研究相应的满足不变性的空间相似性度量模型。

图3-15　遥感图像上多个目标之间存在明显的空间关系特征

一、空间关系表达模型

Egenhofer指出空间关系表达了空间数据之间的一种约束。空间关系描述了遥感图像上地理实体之间存在的一些具有空间特性的关系，一般分为拓扑关系、方位关系和度量关系。其中，拓扑关系和方位关系属于空间关系中的定性关系，度量关系属于空间关系中的定量关系[26]。

1.拓扑关系

拓扑关系指的是拓扑变换下的拓扑不变量，主要描述目标的邻接和关联关系。在拓扑关系形式化描述模型方面，代表性的模型包括4交叉模型(Egenhofer，1991)、9交叉模型(Egenhofer，1993)、基于Voironoi图的9交叉模型(陈军，1999)、空间逻辑模型(RCC)(Randell等人，1992)和空间代数模型(李志林，2002)等。

其中，4交叉模型是由两个空间目标A和B的内部点集、边界点集的交集形成的拓扑关系模型，在交集为φ或者非φ的情况下，可以获得若干种点点关系、点线关系、点面关系、线线关系、线面关系和面面关系。例如，由4交叉模型获取的8种面面拓扑关系为:相离、相接、相交、相等、覆盖、覆盖于、包含、包含于。

Egenhofer等人在4交叉模型基础上构建了经典的9交叉模型，是由两个空间目标A和B的内部点集、边界点集和余点集的交集形成的拓扑关系模型，定义如下:

在交集为φ或者非φ的情况下，可以区分两个空间目标之间的29＝512种拓扑关系，但在实际应用中与之对应的拓扑关系并没有这么多。与4交叉模型相比，9交叉模型比能区分拓扑关系总的种类更多，但是能区分的面面关系也是8种，图3-16给出9交叉模型区分的8种面面拓扑关系及对应的9交矩阵。

图3-16　8种拓扑关系及对应的9交矩阵

针对9交叉模型在空间关系表达方面仍然存在不足的情况，研究人员又提出一些改进模型，如基于维数扩展的9交叉模型(Clementini，1994)、基于Voronoi图的9交叉模型(陈军，1999)等、广义9交叉模型(Abdelmoty A.I.等人)等。

2.方位关系

方位关系描述的是目标在空间上的顺序关系或者位置关系(比如前后、上下、东西、南北等)，是两个空间目标之间互为源目标和参考目标的相互指向关系。常用的方位关系表达模型包括基于几何近似的表达、基于符号投影的表达、基于方向关系矩阵的表达等。

1)基于几何近似的表达

基于几何近似的表达，其基本思想是采用空间目标的几何近似之间的关系代替空间目标之间的关系，例如最小外接矩形(MBR)、最小外接圆(MBC)等，优点是直观、实现简单、计算复杂度低，缺点是空间目标的几何近似之间的关系与空间目标之间的实际关系之间常常会存在不一致的情况。以MBR为例，一个对象的MBR定义为完全包含该对象的矩形，用X和Y方向上的最大值和最小值来标识，如图3-17所示。具体应用中常将MBR作为粗过滤器来判断对象是否满足一定的空间关系。

图3-17　图像中目标(A)的MBR表示

2)基于符号投影的表达

基于符号投影的表达的代表性方法是二维串(2D string)，其基本思想是采用符号投影的方法，将不同空间目标的边界沿着X轴和Y轴做正射投影，生成有顺序关系的字符串来表达目标之间的空间关系，从而将图像对象之间的二维空间关系转换为一维空间关系。应用于图像检索时，首先采用自动或者半自动的方式把图像对象分割出来，然后基于2D String表达对象间空间关系。

2D String定义了三种空间操作符:“＝”，“＜”，“:”，分别表示具有相同投影、左/右关系或者上/下关系、具有相同位置三种空间关系。以图3-18为例，目标之间的空间关系用2D-String来表示的结果为:A＝D:E＜A＝B＜C，A＜B＝C＜D:E。

图3-18　基于2D String的空间关系表达

为了表达图像对象间更复杂的空间关系表达，研究人员提出一些2D String的变种，如2D C-String、2D C＋-String、2D G-String、2D H-String、2D T-String、2D B-String、2D-Be String等，从空间分割、拓扑关系充分表达、计算复杂度等方面进行了更加全面的考虑。

3)方向关系矩阵

方向关系矩阵用关系矩阵的形式描述两个空间目标之间方位关系的细节信息，可以作为空间查询和空间推理的基础。基本思想是:将平面空间划分为9个区域，每个区域称为一个方向片，分别对应一个主方向，如图3-19所示。

图3-19　方向矩阵模型中关于方向片的划分(A为参考目标)

空间目标A和B的方向关系定义为对两个目标的9个方向片求交的之后得到的方向关系矩阵，即

Goyal又对方向关系矩阵进行了进一步的改进，采用源目标在某一方向片区的面积比例代替交集来构建方向关系矩阵，即

4)基于直方图的方位关系表达

基于直方图的空间关系表达以直方图的形式描述图像上两个目标或多个目标之间方位、朝向以及距离的变化的能力，以方位关系表达为主，有时也会包含目标之间的部分类型的拓扑关系表达。例如F-直方图(P.Matsakis，2004)通过计算两个目标之间力的关系反映二者的方位关系；R-直方图(Yuhang Wang，2003)在度量两个目标之间的方位关系时，在角度之外增加了距离标签，以增加拓扑关系(相交和包含)的表达。

5)基于图的方位关系表达

基于图的空间关系表达以节点和边的方式表达图像上的目标及目标之间的空间关系，采用图匹配的方法来衡量空间相似度。例如基于属性关系图(attributed relational graph，ARG)的空间关系表达中，分别用图像中的目标和目标之间的空间关系所对应的属性信息来描述属性图中的节点和边。

3.度量关系

度量关系是用某种度量空间中的度量来描述目标间的关系，如目标间距离。度量关系本身是一种依赖某种具体空间度量的定量空间关系。对于面积、周长、直径等定量的度量关系，所采用的数学描述公式比较统一，可以直接计算。对于距离度量而言，点状目标之间的距离常用欧氏距离、广义距离、契比雪夫距离等来定义；而对于非点状目标而言，距离度量则往往有多种定义，有时会引入模糊理论来进行描述。

Egenhofer等人(2007)对度量关系进行了较为深入的研究。例如，可以采用分割度量描述线/线之间的度量关系(空间目标A的内部、边界和外部(余)被目标B的内部、边界和外部(余)分割的程度)。表3-3给出线/线之间的分割度量所对应的9交矩阵，其中用到了线的长度和有限区域的面积这两个度量概念。

表3-3　基于9交矩阵的线/线度量关系的表达[29]

除了单纯包括线面间度量关系的研究之外，还有一些关于拓扑和度量相结合的空间关系描述方法(邓敏，2002；景黎，2007；吴长彬，2009)。三种空间关系相结合有助于实现目标地物更准确更精细的区分。

二、基于F-直方图的遥感图像多目标方位关系表达及检索

F-直方图提供了一种描述两个目标间方位空间关系的手段，通过计算两个目标之间力的关系来反映两个目标的方位空间关系。

1.基于F-直方图的空间关系表达

如图3-20所示，E表示一个物体或者目标，Δα(v)为一条方向线，其中，α为方向线与参考方向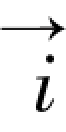的夹角，方向线与物体E相交的部分E∩Δα(v)记作Eα(v)。(www.xing528.com)

图3-20　方向线示意图[30]

一条方向线在通过两个目标时，会分别与两个目标相交，产生两个线段的集合Aθ(v)和Bθ(v)。那么沿着这一条方向线，两个目标间力的作用就是这两个集合中线段间力的合成。对任意角度θ做一组平行线，计算每条平行线上两目标的引力，求和便得到一个力量值。引力由式(3.42)、式(3.43)计算出，式中变量含义如图3-21所示。对θ∈(0，2π)的每一个角度重复上述运算，再利用式(3.44)就得到两目标的F-直方图φAB(θ)。

图3-21　引力计算示意图[29]

图3-22　目标与其旋转和尺度变换结果所对应的F-直方图

旋转和尺度不变性是多目标空间关系描述子必须具备的能力。但是，当图像中的目标发生旋转或尺度变换时，相应的F-直方图的变化表现为平移和幅值的变化。如图3-22所示，当原始目标旋转90°之后，对应的F-直方图向右平移30度；原始目标等比例缩小1倍之后，对应的F-直方图的幅值减小一半。旋转和缩放之后，目标之间的空间关系保持不变。

F-直方图同样适用于描述多目标之间的方位关系。如图3-23所示，增加两个参考物体A和B，然后分别以参考物体A、B为顶点，将目标分成M个区域(M＝20)，每8°为一个区域。对于每个区域i(i＝1，2，…，M)，求参考物体与目标间的F-直方图，计算其力的均值W{i}，代表第i个区域对力的贡献。令

图3-23　多目标间方位空间关系的确定[31]

相似性度量模型如下式:

首先计算出目标图像中目标的空间关系向量S，再计算两图的相似度d(d∈[0，1])。其中，M表示每个参考物体将图像分成的区域数。两组目标越相似，d值越大，当两组目标完全相同时，d＝1。

2.遥感图像多目标空间关系建模及相似性匹配

1)多目标方位空间关系建模

由图3-22可知，当图像中的目标发生旋转或尺度变换时，相应的F-直方图会发生平移和幅值变化。因此，在遥感图像多目标空间关系检索时，需要首先解决F-直方图的旋转和尺度不变性问题。

Scott G.等人(2005)提出，如果能找到一个参考物体，使得这个参考物体与多目标间的相对位置不变，即参考物体随着目标的旋转而旋转，随着目标的平移而平移，就可通过计算参考物体与每个目标的F-直方图来描述这组目标的空间关系，即可解决F-直方图的不变性问题。

旋转不变性的解决方法:首先找到一组目标的中心O，以O为圆心求出这组目标的外接圆，参考物体应在这个外接圆外。然后，利用主成分分析方法(PCA)找出这组目标的主轴方向。寻找主轴方向的方法是:首先，找到每个目标的中心，其坐标分别为(x1，y1)，(x2，y2)，…，(xN，yN)，其中，N为目标的个数，再以向量x＝(x1，x2，…，xN)，y＝(y1，y2，…，yN)为原始方向，取PCA变换后的第一主分量，作为主轴方向e＝(x0，y0)，使参考物体位于主轴方向和圆心O所确定的直线上，这样就可以确定参考物体的具体位置。由于一个参考物体，只可以保证目标在180°以内旋转的相对位置不变，要想获得目标360°旋转的不变性，需确定两个参考物体A和B，这样无论原目标如何旋转，只要参考目标与多目标间的相对位置不变，F-直方图就不会发生改变。

尺度变换不变性的解决方法:分别以参考物体A、B为顶点，将目标分成M个区域(如图3-23所示，其中M＝20)，每8°为一个区域，对于每个区域i(i＝1，2，…，M)，求参考物体与多目标间的F-直方图，计算其力的均值W{i}，代表第i个区域对力的贡献。最后，对空间关系向量S[参见式(3.45)、式(3.46)]进行归一化处理，即可满足尺度不变性。

2)遥感图像多目标空间关系相似性匹配

采用式(3.47)进行基于F-直方图的遥感图像多目标方位关系的相似性匹配，图3-24给出一组匹配结果，数据源来自瑞士某城市的Quickbird卫星影像。首先从中选取一块包含一组简单房屋在内的感兴趣区域(尺寸为255×255像素)，并对其分别进行旋转和尺度变换。可以看出，当原始图像旋转90°或者缩小为原来的1/2，变换前后的F-直方图保持不变，充分表明增加参考物体之后，F-直方图满足了旋转和尺度不变性。

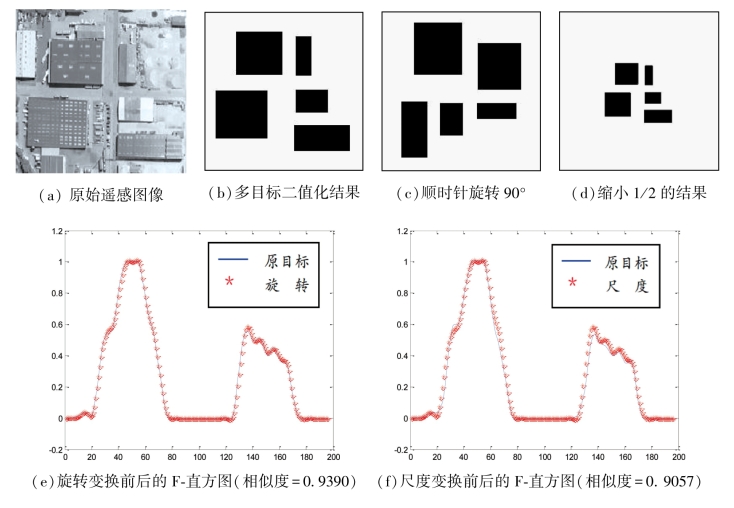
图3-24　多目标尺度变换前后的F-直方图匹配结果

三、基于属性关系图的遥感图像空间关系表达及检索

基于图的空间关系表达包括属性关系图(attributed relational graph，ARG)和空间方位图(spatial orientation graph，SOG)等。其中，ARG模型是一种加权关系图，包括了对原始图像全局信息和局部信息的描述，其抽取和建立是对图像结构信息的高度概括，在基于图像内容和结构的图像检索及目标识别中获得了广泛的关注和应用，如Selim Aksoy(2006)将其用于遥感图像多目标空间关系的表达及检索。

属性关系图由节点和连接节点的边构成。其中，节点表示空间目标，边表示目标之间的空间关系。对遥感图像而言，节点表示构成复杂场景(如建筑物群、港口、机场、油库等)的单一目标，边表示多个单一目标之间的空间关系。

1.基于属性关系图的空间关系表达

2.基于属性关系图的空间关系检索流程

基于属性关系图的检索流程可以描述为如图3-25所示。

(1)采用无监督算法(如边缘流算法)对图像进行分割，并构建所有目标图像的属性关系图。

(2)采用谱嵌入算法(用于边匹配)和子图同构算法(用于节点匹配)实现图像的相似性匹配。如果图之间相似，则光谱嵌入算法的相似性距离GDe和子图同构算法的相似性距离GDn很小，反之亦然。光谱嵌入算法旨在根据边界相似性估算两图像间的距离。光谱图嵌入法运用邻接矩阵拉普拉斯算子得到特征向量，在小范围特征空间中实现光谱嵌入(嵌图)；子图同构算法则是根据图像节点之间的相似性进而得到图像之间的相似性。将谱嵌入算法和子图同构算法相结合得到最后图像之间的相似性。

光谱嵌入公式:

①对于查询图像节点Gq，训练图像节点Gi，与最小非零特征值相对应的特征向量代表嵌图主要组成部分，计算嵌图之间的距离相似度GDe；

②通过查询图像节点Gq，训练图像节点Gi之间相似性距离GDe评估图之间的距离

图3-25　基于属性关系图的图像检索流程图

子图同构公式:

如果Gq不能与Gi中任何节点相匹配，在这种情况下，节点匹配通过估算G Dn(Gi，Gq)得到相应的，进而输出相似性由大到小排序的检索结果。

③返回并输出相似集合。

图3-26给出两组基于属性关系图的检索结果图，并与基于灰度共生矩阵的检索结果进行了对比。以UCMD数据集为例，分别选取棒球场(baseball diamond)和十字路口(intersection)作为查询类别。红色框表示错误检索类别，并在其下注明所属类别。实验结果充分体现了空间关系在遥感图像表达方面的优越性。

图3-26　基于ARG和GLCM的遥感图像检索结果