基于形状特征的遥感图像检索技术

关于形状，至今还没有从几何学、统计学或形态学给出一个确切的定义，使之能与人的感觉相一致。一般认为，在描述图像的内容时，形状特征与颜色特征和纹理特征相比，包含了一定程度的语义信息。形状特征通常采用边缘和区域特征来描述。其中，基于区域的形状描述方法注重几何形状的全局特征，描述形状局部特征的能力相对有限，常采用几何参数，如面积、周长、中心、对称性、散射性等来描述，也可以采用各种矩描述算子来描述，如几何不变矩、Legendre矩、Zernike矩(Zernike moments descriptors，ZMD)、复数矩、正交的Fourier-Mellin矩，以及网格描述算子(grid descriptors)等。基于轮廓的形状描述方法通过比较形状的二维轮廓的接近程度进行形状匹配，具有较强的描述形状局部特征的能力。常用的基于轮廓的形状描述方法有多边形近似(polygonal approximation)、自回归模型(autoregressive models)、傅里叶描述子(fourier descriptors，FD)、曲率尺度空间描述算子(curvature scale space descriptors，CSSD)等。理想的形状描述子应该满足不变性(invariance)、稳定性(stability)、唯一性(uniqueness)及细节检测能力(sensitivity)。

遥感图像上的许多地物目标都有其特定的形状特征。遥感图像的空间分辨率不同，遥感图像形状的含义也不同。在高分辨率遥感图像上，遥感图像的形状代表的是地物目标本身的几何形状；在中低分辨率遥感图像上，图像形状代表的是同类地物目标的分布形状。基于目标形状特征的遥感图像检索，就是通过比较查询图像和遥感图像上目标的形状特征之间的相似性，从而实现对感兴趣目标的快速查找和定位。

图3-11　基于Contourlet域谱直方图的遥感图像纹理特征检索结果

一、基于小波变换的遥感图像形状特征提取

小波变换具有提取多尺度可视化信息的能力，在提取物体形状特征方面引起了人们的关注。将小波变换应用于基于形状的图像检索的方法有:小波重要系数法和方向细节直方图法等，但是通常的基于规则抽样进行离散小波变换获得的小波系数缺少平移不变性。Mallat建议采用小波变换模极大值(wavelet transform modulus maxima，WTMM)来描述信号的奇异点信息，因为小波变换模极大值是在对多尺度小波变换进行不规则抽样的基础上得到的，可以满足平移不变性，这是理想的形状特征描述子必须考虑的一个指标。对于图像而言，小波变换模极大值描述的是图像中目标的多尺度边界。小波变换模极大值边缘检测方法主要利用了小波变换对突变信号的敏感性，以及它在时域和频域很好的定位能力，通过小波进行奇异性分析，可以实现奇异点定位，从而达到边缘检测的目的。除了应用于边缘检测之外，小波变换模极大值还被广泛用于噪声消除、信号重构、特征提取等。

1.小波变换模极大值

若θ(x，y)在整个平面上的积分值为1，且它在x或y为无限远处收敛为0，则定义θ(x，y)为二维平滑函数。现定义两个小波函数φ1(x，y)和φ2(x，y)为:

这样，图像f(x，y)的小波变换的两个分量在尺度为s时的定义为:

对于二进制小波变换:

可以看出，式(3.21)中小波变换的两个分量正比于梯度矢量∇(f*θ2j)(x，y)的两个分量，在任一尺度2j，梯度矢量的模为:

梯度矢量与水平轴的夹角为:

f*θ2j(x，y)上变化剧烈的点是沿着梯度方向A2j f(x，y)上模M2j f(x，y)为局部极大值的那些点，我们只需记录下这些模极大值的位置以及相应的模M2j f(x，y)和角度A2j f(x，y)的大小即可。

Mallat已经证明:

(1)小波变换模极大值方法具有平移不变性；

(2)如果信号本身的傅里叶变换是带限的且小波函数φ是紧支撑的，则小波变换模极大值的表示是完备的。

在实际应用中，小波变换最终体现在滤波器对信号的滤波上，可通过两个互相正交的高通、低通滤波器的递归循环卷积得到，其二维空间域的离散形式为:

式中，S2j f(x，y)表示信号的低通平滑分量，反映了图像的离散概貌，j＝0时即为原始图像，序列{hk}、{gk}分别为低通、高通滤波器的脉冲响应。

2.基于小波变换模极大值的遥感图像边缘检测

基于小波变换模极大值的遥感图像边缘检测的步骤可以总结为:

(2)根据式(3.22)和式(3.23)计算模M2j f(x，y)和角度A2j f(x，y)；

(3)记录小波变换域中模是局部极大值并且大于预设阈值的点，得到尺度从0到J的多尺度边缘图像；

(4)特征向量归一化。

特征向量归一化的目的在于消除由于特征向量中特征元素不统一而引起的欧氏距离空间相似性度量偏差。如果将目标的形状特征向量记为F＝[f1 f2…fN]T，其中N是特征元素的个数，设遥感图像目标库包含M个目标，用Fi＝[fi，1 fi，2…fi，N]T表示第i(i＝1，2，…，M)个目标的特征向量，则遥感图像目标形状库可以表示为一个M×N特征矩阵F＝{fi，j}，其中fi，j是Fi的第j个特征元素。F的每一列是长度为M的特征序列，即为Fj。设Fj是一个高斯序列，计算出其均值μj和标准差σj，然后利用公式(3.25)就可以将原特征序列归一化为N(0，1)分布的序列。

图3-12为一幅遥感图像(尺寸为608×384像素)基于小波变换模极大值方法的边缘检测结果。其中，尺度J＝1～3，小波变换选用二次样条小波，滤波器为

可以看出，小波变换模极大值方法可以检测出目标在不同尺度上的轮廓信息，随着尺度J的增加，过滤掉的噪声增多，但图像的边缘信息保留了基本的完整性。

图3-12　原始遥感图像及基于小波变换模极大值的边缘检测结果

二、基于多尺度形态学的遥感图像形状特征提取

1.形态学理论基础

数学形态学(mathematical morphology)是由法国数学家G.Matheron和J.Serra在20世纪60年代中期创立的一种建立在集合代数基础之上，用集合论方法定量地描述几何形状和结构的学科。数学形态学历经近四五十年的发展，至今已形成一个比较完备的理论体系，并且已经在图像处理、模式识别和计算机视觉等领域获得了非常广泛的应用，如抑制噪声、图像分割、特征提取、边缘检测、形状识别、图像恢复和重建等。用数学形态学方法进行图像边缘检测时，算法简单同时能够较好地保持图像细节特征，可针对不同的图像及要检测的不同目的灵活地选取不同形式的结构基元。

数学形态学的基础是二值形态学，最基本的二值形态学算子有4种:膨胀(dilation)、腐蚀(erosion)、开(opening)、闭(closing)。灰度形态学是二值形态学应用于灰度图像的推广，图像的函数空间从二维平面推广到三维空间，函数的值域从{(0)，(1)}推广到[0，255]。灰度形态学的膨胀、腐蚀、开、闭运算的定义如下:

灰度形态膨胀和腐蚀运算相当于局部最大和最小滤波运算，开、闭运算可构成灰度形态学梯度。灰度膨胀运算和灰度腐蚀运算均以结构元素为模板。其中，灰度膨胀运算可减弱或消除灰度值低的细节信息，同时增强灰度值高的区域边缘信息；灰度腐蚀运算可降低边缘部位灰度值高的细节信息，收缩灰度值高的区域边缘信息。针对不同的灰度形态基本算子的特点，可以构造不同的形态边缘检测运算形式，同时考虑到形态运算的全方位特性及多结构元多尺度分析特性，从而可构造出优良的形态边缘检测算法。

2.基于多尺度形态学的遥感图像边缘检测

由于形态算子实质上是表达物体或形状的集合与结构元素之间的相互作用，结构元素的形态就决定了运算的形态信息，多尺度形态学用于图像处理的基本思想就是通过改变结构元素的尺度，对图像进行多尺度分析，从而提取图像在不同尺度下的形状特征。(www.xing528.com)

一般来说，物体的不同尺度会对应不同层次的结构特征，而同一结构特征在不同的尺度层次上可能会有不同的表现，因此对物体本身的描述可以采用不同尺度层次的局部特征表征。多尺度形态学边缘检测算子利用不同尺度的结构元素提取图像的边缘特征，小尺度的结构元素去噪能力弱，检测边缘细节信息的能力较强；而大尺度的结构元素虽然检测到的边缘较粗，但去噪能力强，如果采用多个不同尺度的结构元素提取不同尺度的图像边缘信息，就可合成得到较理想的边缘图像。

多尺度形态学边缘检测算法步骤如下:

(1)用不同尺度的结构元素检测原始图像不同尺度的边缘信息。

对应于D1，D2，D3，D4，尺度n下的结构元素为nD1，nD2，nD3，nD4，且Drodn＝nDrod1，此时构造尺度为n的边缘检测算子为:

式中，

(2)采用式(3.27)合成不同尺度的边缘信息，生成边缘图像f′(x，y)。[k，l]表示尺度n的取值范围，wn为尺度n的边缘信息所占权重。

(3)采用非极大值点运算方法提取边界点:对于如式(3.30)所示的3×3矩阵，当像素a满足条件式(3.29)，则认为a为边缘点，否则用min{a1，a2，a3，a4，a5，a6，a7，a8}代替a。

(4)细化边界图，获取目标骨架图。

图3-13为一幅遥感图像(尺寸为608×384像素)基于多尺度形态学方法的边缘检测结果。其中，选用的结构元素如图3-13(a)所示，图(c)是边缘检测结果为尺度1和尺度3的加权合成结果，权值分别为0.4和0.6。可以看出，多尺度形态学方法通过叠加不同尺度的边缘检测结果，可以获取目标在不同尺度上的轮廓信息。

图3-13　原始遥感图像及基于多尺度形态学的边缘检测结果

三、基于不变相对矩的形状相似性匹配

在图像形状识别中，已经获得比较广泛应用的形状描述方法包括Hu不变矩描述子和傅里叶描述子等。其中，通过对Hu不变矩及不变矩快速算法的扩展而提出来的相对矩，不仅能够满足区域和结构的形状平移、尺度、旋转不变性条件，而且对于封闭及不封闭结构(结构在这里指表示目标形状的单像素骨架)均能有效识别，因而更具有普遍性。

1.区域不变矩

一幅数字图像f(x，y)的p＋q阶矩和p＋q阶中心矩定义为:

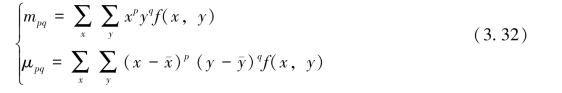
重心坐标(¯x，¯y)的计算:

这种几何矩和几何中心矩可用于描述区域的形状。Hu提出了7个不变矩，并且已经证明了这组矩满足平移、旋转、尺度不变性。

式中，

2.不变矩快速算法

为了快速计算区域不变矩，Chen提出了利用区域边界来计算区域矩的快速算法，将几何矩和几何重心矩分别定义如下:

式中，C代表一条平滑曲线，¯x＝m10/m00，¯y＝m01/m00，(p，q＝0，1，2，…)，经过证明，当用式(3.37)替代式(3.36)时，式(3.35)的7个矩描述子仍然满足平移、尺度、旋转不变性。

3.相对矩

由于区域矩的公式不能直接用来计算边界矩，为了进行轮廓特征的相似性度量，需要定义边界矩，因此需要对式(3.34)不变矩计算公式进行修正，式(3.33)中与区域有关的面积比例因子μ00失效，因此式(3.32)中的矩描述子不再满足尺度不变性。

为了得到适用于区域、封闭和不封闭结构的统一不变矩特征计算公式，王波涛等人(2001)提出利用矩之间的比值去掉比例因子μ00，从而使不变矩公式与面积或结构的比例缩放无关，而仅与几何形状有关。由此得到相对矩的计算公式:

相对矩描述子的优点在于其不仅具有结构平移、尺度、旋转不变性，而且统一了区域和结构的矩特征计算。

基于形状特征的遥感图像特征检索的步骤可以总结为:

(1)构建多源遥感图像数据集；

(2)提取遥感图像目标区域的轮廓边界信息作为形状特征；

(3)将查询图像的形状特征与待检索遥感图像的形状特征进行相似性匹配；

(4)根据距离值返回查询结果。

图3-14给出4组基于形状特征的遥感图像检索结果。以UCMD数据集为例，选取了十字路口(intersection)、中型住宅区(medium residential)、高速路(runway)、港口(harbor)作为查询类别，对比了基于小波变换模极大值结合相对矩和基于多尺度形态学结合相对矩的形状特征检索性能，红色框表示检索错误类别，并在其下注明所属类别。可以看出，与基于小波变换模极大值结合相对矩的检索方法相比，基于多尺度形态学结合相对矩的方法具有更好的局部特征表达能力，在查询图像为立交桥和中型住宅区时检索性能更好。但是两种方法在解决类间相似的问题时都存在明显局限性。

图3-14　基于形状特征的遥感图像检索结果