基于纹理特征的遥感图像检索技术

自从Haralick在1973年首次将纹理特征应用于遥感图像的分类以来，越来越多的研究认为，纹理特征是遥感图像分割、分类、目标识别等应用中最为基本和重要的特征之一。如前所述，纹理是一种不依赖于颜色或亮度的、反映图像中同质现象的视觉特征。在遥感图像中，纹理主要是由地物特征如森林、草地、农田、城市建筑群等产生。在高分辨率影像分析和识别中，特别是当遥感图像上目标的光谱信息比较接近时，纹理信息对于区分目标具有非常重要的意义。

传统的纹理分析方法一般可以分为统计法、结构法、模型法和变换域法。

(1)统计法:是基于像素及其邻域的灰度统计特性如一阶、二阶或高阶矩的纹理分析方法。经典的统计法包括灰度共生矩阵法、空间相关矩阵、自相关函数法、纹理谱统计法等。统计法思想简单、易于实现，但大多存在纹理特征识别能力一般且计算量大、实时性差的缺点。

(2)结构法:认为纹理由纹理基元组成，不同类型、不同大小和方向的纹理基元决定了纹理的表现形式。结构法假设纹理基元可以分离出来，并按某种排列规则进行排列，以基元特征和排列规则进行纹理分割。具体方法包括数学形态学法、句法纹理分析等。

(3)模型法:假设纹理是以某种参数控制的分布模型方式形成的，从纹理的实现来估计计算模型参数，以此描述不同的纹理特征，模型参数的估计是模型法的核心问题。常用的模型法包括分形方法和马尔可夫随机场方法。分形方法和马尔可夫随机场方法是目前应用最广、效果较好的模型分析法。分形方法主要表征了图像物理的自相似程度和粗糙性特征，分数维作为分形的重要特征和度量，把图像的空间信息和灰度信息有机结合起来。马尔可夫随机场则通过任意像素关于其邻域像素的条件概率分布来描述纹理，提供了一种表达空间上相关随机变量之间的相互作用的模型，可以和模拟退火、贪婪算法等优化算法结合应用。

(4)变换域法:基于人的视觉具有多通道和多分辨率的特征，认为纹理作为一种局部邻域信息，具有层次性、尺度性，纹理特征应能反映纹理的多尺度特征。建立在时、频分析和多尺度分析基础之上的方法能提取多层次纹理信息，具体算法如Gabor滤波器法、小波变换，以及在小波变换基础上发展起来的Contourlet变换、Curvelet变换等。

以下介绍几种代表性的纹理特征描述方法。

一、灰度共生矩阵

灰度共生矩阵(gray-level co-occurrence matrix，GLMC)是一个矩阵函数，由图像中某个方向上相隔一定步长的两个像素点确定，通过计算两个像素点灰度的相关性来反映图像的纹理特征。灰度共生矩阵的大小由图像的灰度级确定，对于灰度级为k的图像，灰度共生矩阵为k×k大小的矩阵。在一幅n×m大小的图像中，灰度共生矩阵中每个元素的计算公式如下:

式中，I(x，y)和I(x′，y′)代表两个灰度值，x′和y′通过初始点坐标x，y，步长d和角度θ计算得到。θ一般设置为0°、45°、90°和135°。

如图3-5所示，当步长为1，θ为90°时，对于左边的原始图像，统计图像中所有的灰度值为(1，1)的像素对得到P(1，1，1，90°)为1，统计图像中所有的灰度值为(1，2)的像素对得到P(1，2，1，90°)为2，依次计算8个灰度级的元素，可得到灰度共生矩阵。

图3-5　灰度共生矩阵(GLMC)计算示意图

二、2D Gabor小波滤波器

Gabor变换是D.Gabor针对傅里叶变换在时变信号、非平稳信号分析中的不足(既不能确定某些频率成分发生在哪些时间内，也不能表示某个时刻信号频谱的分布情况)，于1946年提出的一种采用高斯函数作为窗函数的局部化傅里叶函数，广义Gabor变换又称短时傅里叶变换。Gabor变换的时间分辨率和频率分辨率满足测不准原理(Uncertainty Principle)，也就是说，Gabor变换具有最小的时频窗，能做到具有最精确的时间-频率的信号局部化描述。作为一种在方向和频率上具有选择性的带通滤波器，Gabor滤波器可以通过改变方向、带宽和中心频率，形成一组不同频率、不同方向的多通道滤波器组，从而用尽可能少的滤波器表示图像完整的频谱信息，尽可能地覆盖图像的频域空间。利用多通道的滤波器，可以将图像映射到Gabor滤波器的不同频率、不同方向的通道中，再通过滤波器响应值变化的急缓程度来区分图像在不同频率、不同方向上的纹理特征。总之，Gabor滤波器具有时域和频域的联合最佳分辨率的良好性质，较好地模拟了人类视觉系统的视觉感知特性，已经被证明应用于纹理分析中非常有效。

2D Gabor函数是一个经过复数正弦函数调制的二维高斯函数，通过设计2D Gabor函数、带通区域中心频率、方向参数和尺度参数等，可以构造出一个具有方向和频率选择性的带通滤波器组，从而将图像信息分解到多个不同方向和不同频率的子带，实现特征提取。如果采用母Gabor小波作为2D Gabor函数，表达式如下:

作傅里叶变换:

式中，θ＝kπ/K表示滤波器的方向，k和s分别表示多尺度分解中的方向和尺度参数，K和S表示滤波器组的总方向数和总尺度数，a－S为尺度因子。设Ul和Uh分别表示最低中心频率和最高中心频率，滤波器组参数计算公式如下:

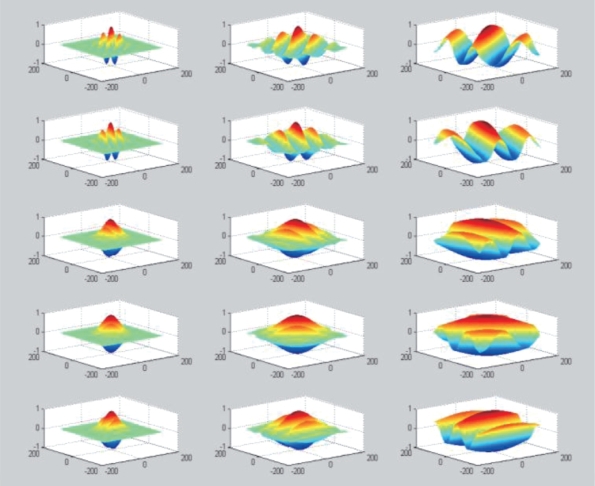
图3-6　Gabor滤波器gx，k(x，y)在3个尺度(S＝3)和5个方向(K＝5)上的实分量

图3-7　Gabor滤波器gx，k(x，y)在不同尺度和不同方向上的实部

对于给定图像I(x，y)，其Gabor小波变换可以定义为:

则纹理特征向量为:

(www.xing528.com)

其中，μmn和σmn分别表示变换系数的均值和方差，计算公式为:

距离计算公式:

其中，α(μmn)和σ(σmn)用来实现归一化。

图3-8给出了一组基于2D Gabor小波滤波器的遥感图像纹理特征检索结果。以UCMD为数据集为例，选取农田(agricultural)作为查询类别。可以看出，基于2D小波滤波器的遥感图像纹理特征包含了丰富的局部区域方向信息，因此十分适合于检索具有方向梯度信息的遥感图像。

图3-8　基于2D Gabor小波滤波器的遥感图像纹理特征检索结果

三、Contourlet变换

小波变换是在20世纪80年代中期发展起来的应用数学理论，具有良好的时、频局部变化特征和多尺度特性。小波变换及其理论分支能够提供对不同尺度的纹理的有效分析，为纹理的时频多尺度分析提供了一个精确而统一的框架，提供了遥感图像纹理特征多尺度分析的有效手段。随着人们对于小波变换在图像细节信息表达方面的局限性的认识，出现了以Curvelet变换和Contourlet变换为代表的新一代多尺度几何分析工具，以其在图像多方向和多尺度纹理特征表达方面的独到优势，获得了图像处理和分析领域众多研究人员的青睐。

Contourlet变换是Minh.N.Do和Martin.Vetterli在2002年提出的一种新的多尺度几何分析(multiscale geometric analysis，MGA)工具。Contourlet变换是一种从多尺度、多方向的角度来捕获图像固有几何结构信息的图像表示方法，满足各向异性尺度关系，有很好的方向性。Contourlet变换在表达图像时可以同时满足视觉信息描述的三个基本要素:尺度、空间和方向信息，对于图像边缘轮廓和纹理特征的表达有独到的优势。Contourlet的优秀特性使其一经提出就得到了图像分析和处理领域众多研究人员的高度重视，其在遥感图像方面的兴趣大多集中在融合、分类、压缩和检索。

Contourlet变换在获取不同方向细节信息方面的能力，使其在遥感图像纹理特征提取方面具有得天独厚的优势。Contourlet变换中，可以根据需要设置不同的变换尺度参数R和方向尺度参数l，当R＝3时，Contourlet变换的方向滤波器组将图像分级为2l个方向子带，一次3级Contourlet分解可以得到14个方向的高频子带信号。图3-9给出一幅原始遥感图像及其3级Contourlet分解效果图(包括一个低频子带信号和14个方向的高频子带信号)。

图3-9　遥感图像的Contourlet多尺度多方向分解

直方图是近似概率分布的基本统计方法，谱直方图包含了滤波器组响应的边缘分布特征。一幅图像的谱直方图，实际上是某一滤波器的频率响应和多滤波器组的集成响应在边缘分布上的一组向量组成。Contourlet域的谱直方图向量能够在多分辨率尺度上由粗到细的表征图像，并且能够克服一阶统计矩在表达变换系数时仅考虑变换系数统计特性的不足。Contourlet域谱直方图定义如下:

给定一个图像窗口W和一组Contourlet变换带通子带W(α)。子带W(α)的谱直方图计算公式为:

式中，δ(·)为狄拉克函数，v为子带内像素矢量。选择多个滤波器(1，2，…，K)进行滤波操作，可定义图像窗口W的谱直方图向量为:

式中，组成这一组直方图的变换域系数假设是相互独立的。因为每个滤波反映的边际分布都是一个概率分布，因此采用K-L距离离散度的最佳近似值——χ2统计量来定义两个光谱直方图HW1和HW2之间的距离为:

图3-10　遥感图像基于Contourlet变换的谱直方图

图3-10给出两幅遥感图像及其对应的3级分解14个方向的高频谱直方图(变换尺度参数R＝3，其方向参数l＝[1 2 3])，14个方向的纹理特征均归一化在0～63范围之内。对比可以看出，这两幅遥感图像具有不同的纹理特征，图像的Contourlet域谱直方图表现出明显的形态各异性质。

基于Contourlet的遥感图像纹理特征检索的步骤可以总结为:

(1)构建多源遥感图像数据集；

(2)对数据集中所有图像进行Contourlet分解，构建基于谱直方图的纹理特征库；

(3)对Contourlet变换低频系数进行归一化处理并表示为谱直方图，计算查询图像和目标图像的低频谱直方图之间的距离，实现粗过滤；

(4)对Contourlet变换得到的多尺度多方向高频系数进行归一化处理并同样表示为谱直方图，计算查询图像和目标图像的高频谱直方图之间的加权距离，实现精确检索；

(5)返回查询结果。

图3-11给出3组基于Contourlet变换的遥感图像纹理特征检索结果，以AID数据集为例，分别选择农田(farmland)、商业区(commercial)和池塘(pond)作为查询类别。对图像进行contourlet变换时，Contourlet分解方向参数l＝[1 2 3]，滤波器为“9-7”塔形分解和方向滤波器组。红色框表示错误检索类别，并在其下注明所属类别。可以看出，基于Contourlet变换的遥感图像纹理特征充分了考虑Contourlet变换各子带的边缘分布，因此更适用于包含大量结构性边缘信息的高分辨率遥感图像。