计算实例和M文件详解

1.编制绘制6种典型曲线的M文件

运算过程：

系数b=2.000000

输出的双曲线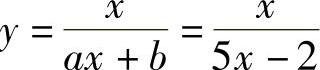苴他运算过程省略。输出的六种图形如图16一所示。典型曲线形态如图16-20和图16-21所示。

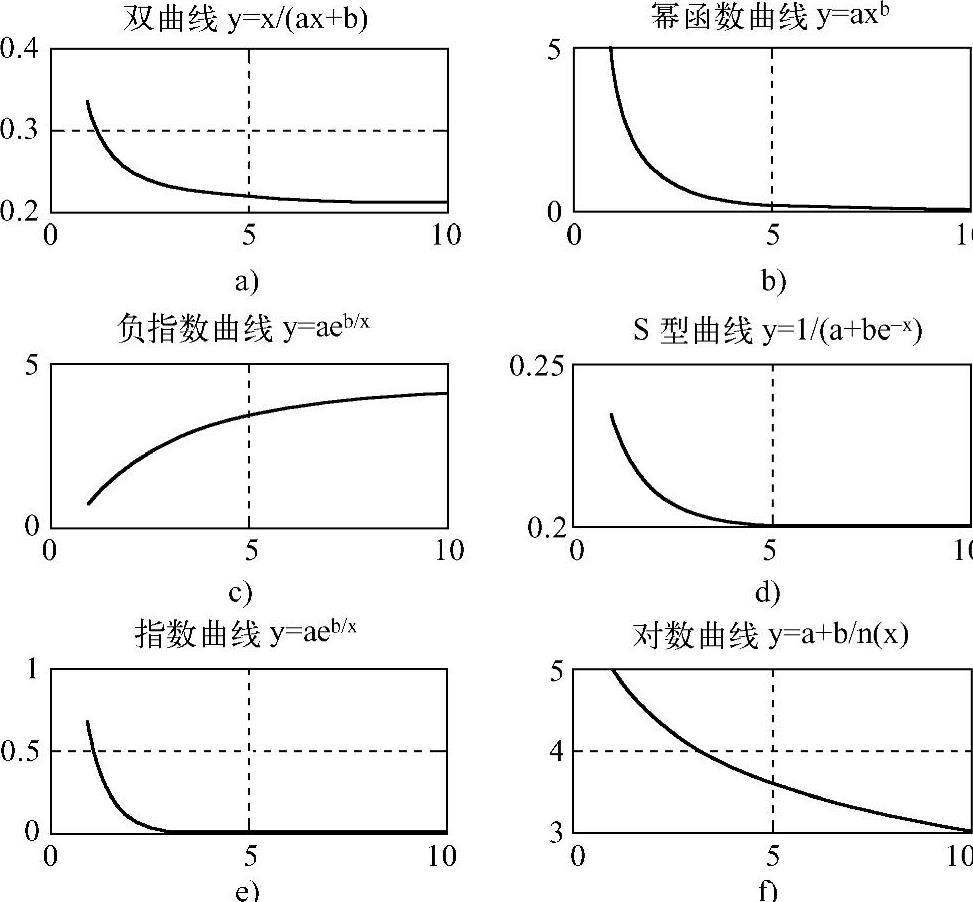
图16-20 b<0时六种典型曲线形态

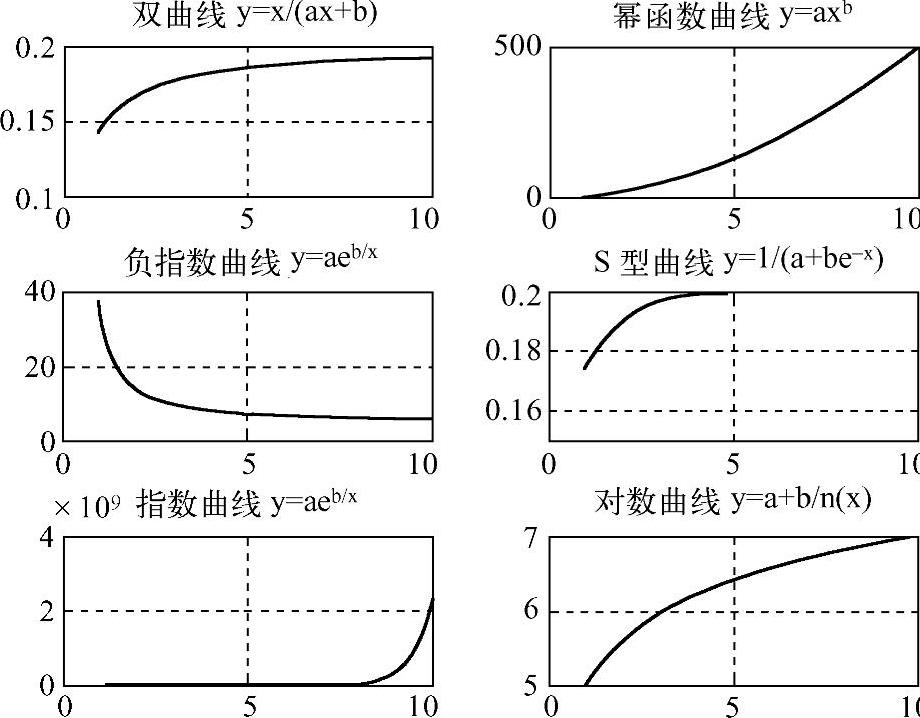
图16-21 b>0时六种典型曲线形态

2．编制典型曲线拟合的M文件

1)利用“switch-case-end”分支结构语句，绘制六种典型曲线与试验观测数据图形对比，从而判定曲线类型。

2)根据fH1线类型进行变量代换。

3)通过计算变量的均值、离差平方和、乘积平方和，确定回归系数。

4)根据曲线类型进行拟合系数代换。

5）通过计算剩余平方和、剩余标准误差和相关指数进行拟合效果与精度的检验。

6）利用“plot”语句绘制拟合曲线，并且与实验观测数据离散点图进行直观比较。

例16-9 已知标准圆柱齿轮复合齿形系数Y_FS与齿数（当量齿数）z（z_v）的关系，见表16-2。

表16-2 标准渐开线外齿轮（α_n=20°、h_a^*_n=1.0）的复合齿形系数

试将其拟合为函数曲线Y_FS=f（z_v）。

表16-2的数据图形如图16-22所示。经过与图16-19所示的典型曲线形态比较可知，应将其拟合为双曲线（b<0）。拟合计算结果得到曲线方程

经检验，拟合的标准误差是σ=0.022984，相关指数是R²=0.996424，这说明拟合效果好，精度高。

运算结果：(www.xing528.com)

输出圆柱齿轮复合齿形系数Y_FS与当量齿数Z_V的关系线图是双曲线[式（16-32）]，如图16-22所示。

3.编制多项式拟合的M文件

1）利用交互式函数polytool（x，y，1），确定多项式拟合的阶数。

2）利用函数[p，S]=polyfit（x，y，m）可直接求出m阶多项式的系数向量p有关信息S。

3)利用函数[yh，delta]=polyconf(p，x，S)或yh=polyval(p，x)求出拟合函数值yh。

4)进行拟合效果与精度的检验。

5)绘制拟合多项式曲线。

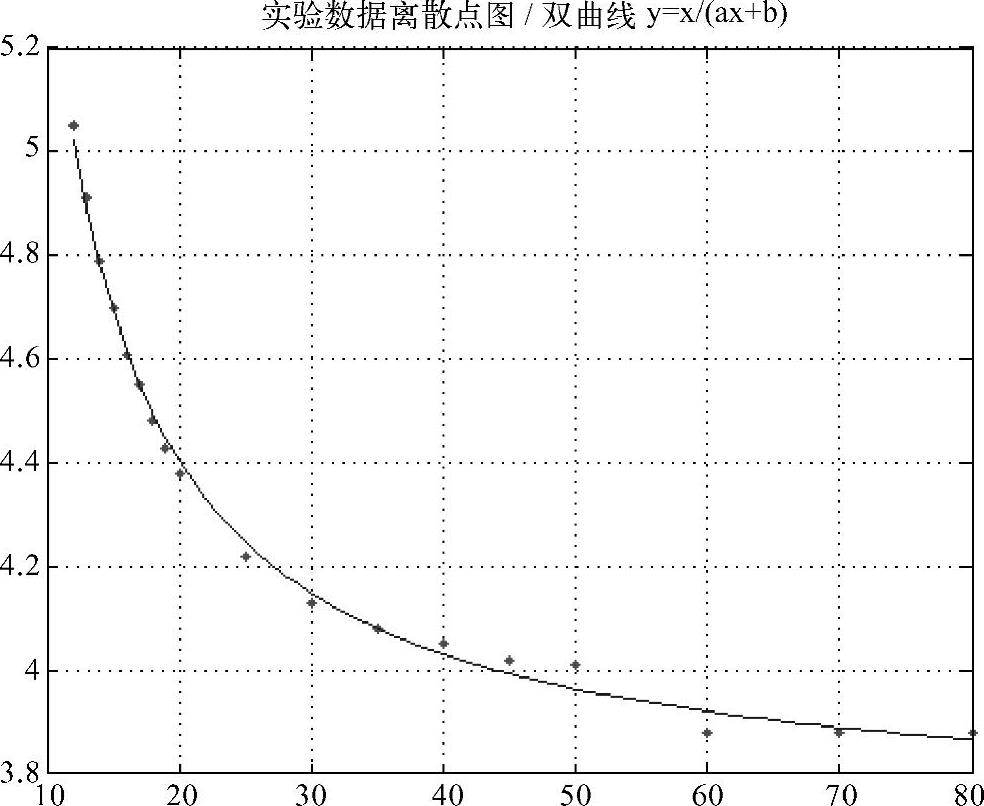
图16-22 圆柱齿轮复合齿形系数与当量齿数的关系

例16-10 已知螺旋副的效率η与导程角λ的关系，见表16-3。

表16-3 螺旋副的效率η与导程角λ的关系

试将其拟合为多项式曲线_η=a₀+a₁λ+a₂λ²+a₃λ³+…。

表16-3的数据图形如图16-24所示，在拟合动态过程中观察拟合图形。当取四阶多项式时，置信区间最小，得到相应的多项式方程是（数据只保留7位小数）

η=-0.0000001+0.0000239λ-0.0014875λ²+0.0429430λ³+0.3271429λ⁴ （16-33）

经检验，拟合的标准误差是α=0.001974，相关指数是R²=0.999369，这说明拟合效果好，精度高。

运算结果：

输出螺旋副效率_η与导程角λ关系的多项式线图[式（16-33）]，如图16-23和图16-24所示。

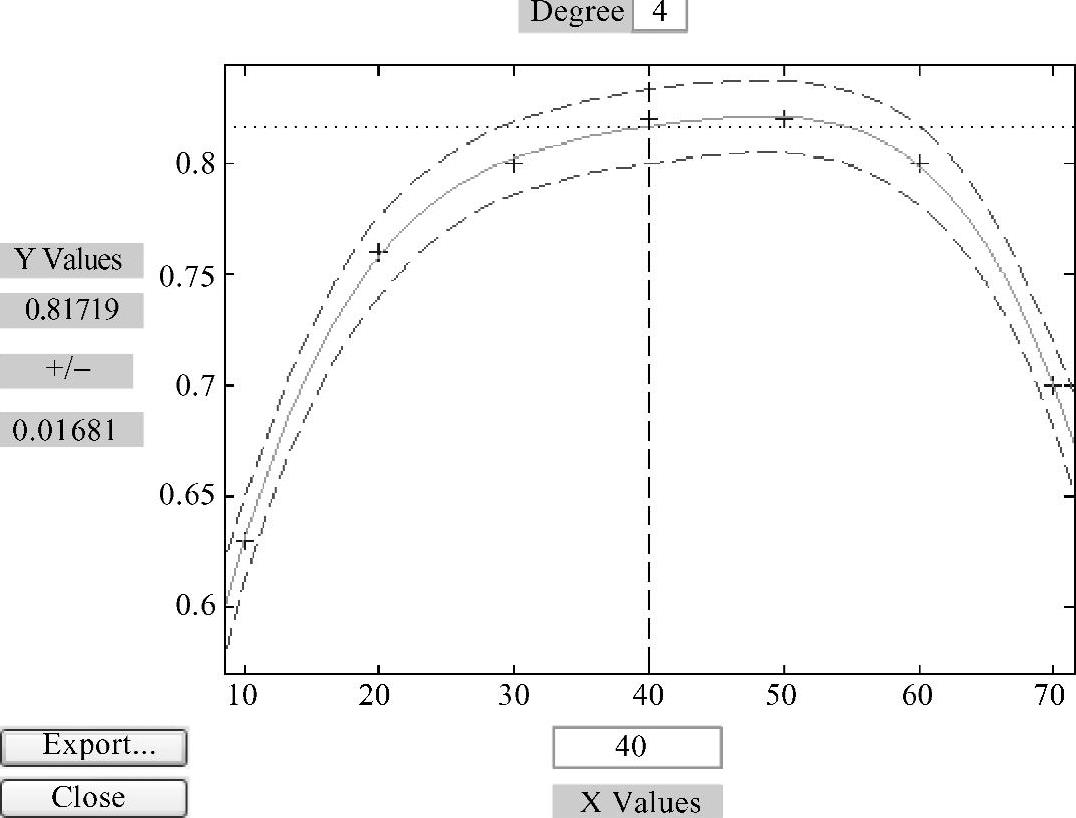
图16-23 螺旋副效率与导程角关系的多项式拟合

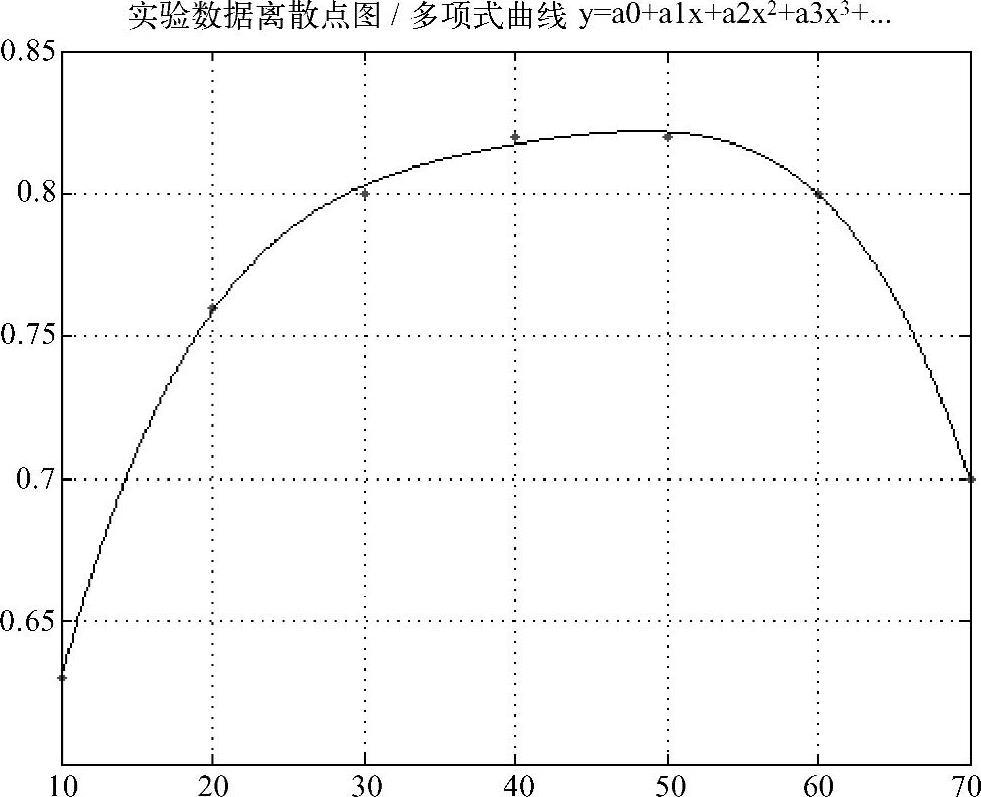
图16-24 螺旋副效率与导程角关系的拟合曲线