【摘要】：显著性检验 统计量如果F≥F0.01，认为回归是高度显著的；如果F≥F0.05，认为回归是显著的；如果F≥F0.01，认为回归是不显著的，y对x线性关系不密切。应当指出，在大多数工程实际问题中，若变量之间的关系是某种曲线关系，就需要进行实验数据的曲线拟合。一般首先确定函数类型，然后通过变量代换将其转换为直线拟合问题：或将曲线拟合问题转化为多项式回归的问题。
式中，回归系数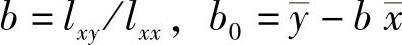
；x离差的平方和
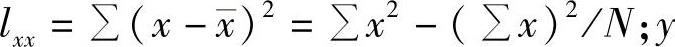离差的平方和
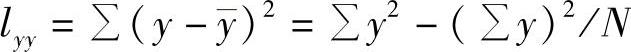，即是总离差平方和S；x和y离差乘积的和
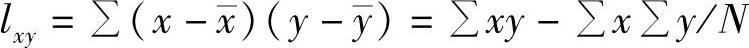；x和y是观察值，
是其均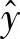值，
是拟合值。
（2）方差分析 总离差平方和
式中，回归平方和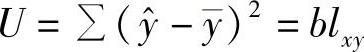
，反映观察值x和y线性相关对y的变差的影响；剩余平方和
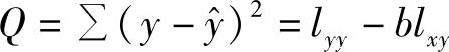，反映试验误差等其他因素对y的变差的影响。
（3）显著性检验 统计量
如果F≥F0.01（1，N-2），认为回归是高度显著的（在0.01的水平上显著）；如果F≥F0.05（1，N-2），认为回归是显著的（在0.05的水平上显著）；如果F≥F0.01（1，N-2），认为回归是不显著的（在0.10的水平上显著，可信赖程度为90%），y对x线性关系不密切。
利用回归方程，可以在一定显著性水平上确定与x对应的y的取值范围。
（4）剩余方差和剩余标准误差(www.xing528.com)
1）相关系数
2）剩余方差（剩余均方差）
它反映了排除x对y的线性影响后（或者当x固定时），衡量y随机波动大小的一个估计值。
3）剩余标准误差（剩余标准偏差、剩余标准离差）
它用来衡量所有随机因素对y的一次性观测平均变差的大小，σ越小回归直线精度越高。
应当指出，在大多数工程实际问题中，若变量之间的关系是某种曲线关系，就需要进行实验数据的曲线拟合。一般首先确定函数类型，然后通过变量代换将其转换为直线拟合问题：或将曲线拟合问题转化为多项式回归的问题。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
