建立数学模型优化工艺参数

例16-8 在M1080无心磨床上磨削轴瓦492Q外圆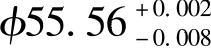，表面粗糙度R_Z=2μm，机床主电动机功率P_C=13kW。按磨削效率最高的要求，选择精磨工序最佳工艺参数。

1.确定设计变量

磨轮转速n=1300r/min，磨轮型号为GB60^#ZR₂A·P500×150×305，导轮型号为GB60^#ZR₂X·PSA300×150×127，有八级转速n_r=13r/min、17r/min、23r/min、30r/min、40r/min、53r/min、71r/min、94r/min。

可以参加优化的独立设计变量为

其中，t为磨削深度，单位为mm。

2.建立目标函数

以每分钟金属切除率最大化，即其负值最小化作为设计目标

minf（X）=10³/（x₁x₂x₃） （mm³/min）

3.确定约束条件

1）为了限制工件的表面粗糙度，工件磨削表面最大高度H_max不超过R_Z，即

式中，u是由砂轮特性决定的切削刃平均间隔，对某种砂轮用插值法求出u=0.22mm；λ是磨轮磨刃半顶角，取λ=53°；d_r是导轮直径，d_r=500mm；B_w是工件宽度，B_w=28mm；v是磨轮线速度，v=10^-3π500×1300=2042m/min；v_w是工件线速度，根据机床导轮有八级转速的变化范围n_r=13～94r/min，得到v_w=12.241～88.579m/min；K_h是表面粗糙度系数，用以考虑由于磨削振动、磨轮磨粒磨损和堵塞等因素造成工件的磨削表面最大高度H_max的实际值是计算值的几十倍，一般取K_h=40～100，这里根据实验统计资料取K_h=80。

经过整理，得到约束方程

2）防止磨削烧伤的约束条件

式中，C_b是由工件材料和磨轮种类决定的磨削烧伤临界系数，C_b=1920m·mm/min；t是磨削深度，t=0.002～0.03mm。(www.xing528.com)

经过整理，得到约束方程

3）在保证工件不产生磨削烧伤的前提下，磨轮有一定的耐用度

式中，C_T是工件材料系数，对于末淬硬钢C_T=2550，淬硬钢C_T=2260；T_b是磨轮耐用度的适用值，按照精磨技术条件取T_b=30min。

经过整理，得到约束方程

4）切削动力不能超过磨床主电动机的额定功率

0.0358（d_wv_αt）^0.7-ηP_C≤0 （16-18）

式中，η是磨床主电动机到主轴之间的传动效率，η≈0.95。

经过整理，得到约束方程

5）按照精磨技术条件，工件的轴向速度v_a≤2000mm/min，即

6）切削加工前工艺参数的边界条件。工件的形状精度（如圆度和圆柱度等）由磨床本身的设计要求、对托板形状与尺寸的选择、导板的调整、磨轮和导轮的修整等来保证。

工件的尺寸精度要根据具体磨削系统刚度，每磨削一批工件时磨轮的径向磨损量的情况，及时修整磨轮，并且改变最终加工位置，以使工件磨削尺寸重新位于公差带中心来保证。因此，边界约束条件是：

这是一个有11个约束条件（其中，g₁（X）～g₅（X）是性能不等式约束，g₆（X）～g₁₁（X）是边界不等式约束）的三维非线性优化设计问题。