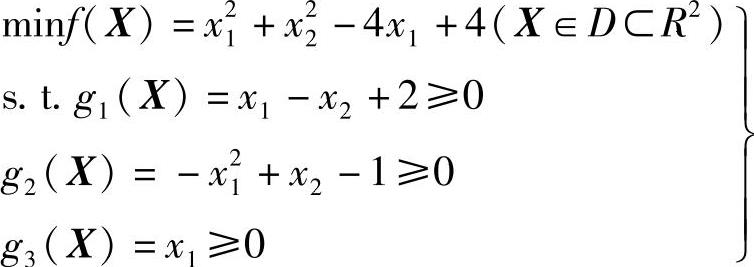
该问题的目标函数f（X）的等值线是以（2，0）为圆心的同心圆族。如图16-1和图16-3所示，约束函数g1（X）的等值线是与二维设计平面上X1轴正向成45°角的斜线族；约束函数g2（X）的等值线是以二维设计平面上X2轴为对称轴、开口向上的抛物线族；约束函数g3（X）的等值线是与二维设计平面上X2轴平行的直线族。显然，图中约束函数g1（X）=0和g3（X）=0时的两条直线，与g2（X）=0时的一条抛物线所围成的封闭区域，就是二维设计平面中的可行域D奂R2。
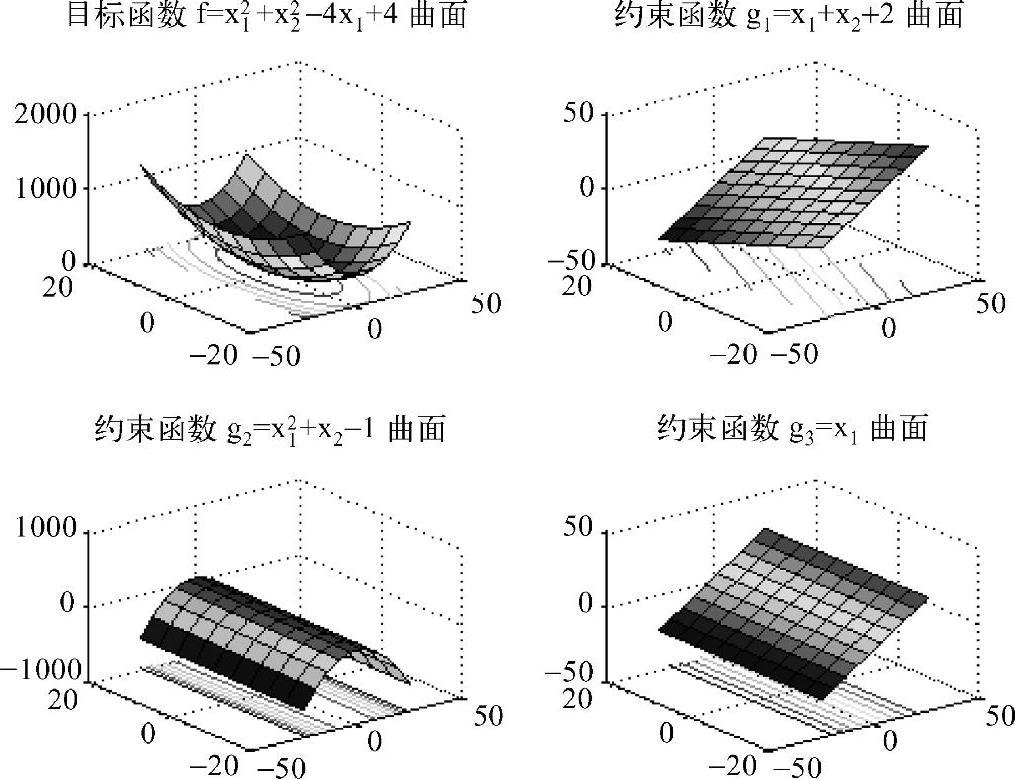
图16-1 二维约束优化问题的目标函数和约束函数曲面（例16-1）
图16-2所示是单独绘制的目标函数和约束函数各个曲面图，可见约束曲面g1（X）、g2（X）和g3（X）与二维设计平面X1OX2一般并不是正交状态。
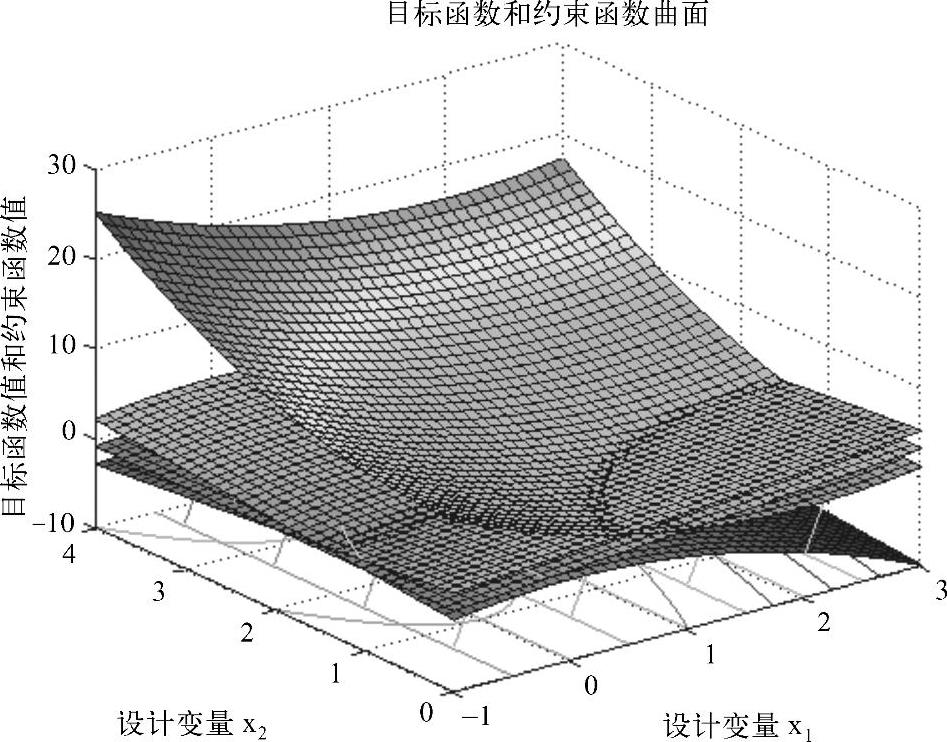
图16-2 二维约束优化问题的目标函数和约束函数曲面组合（例16-1）
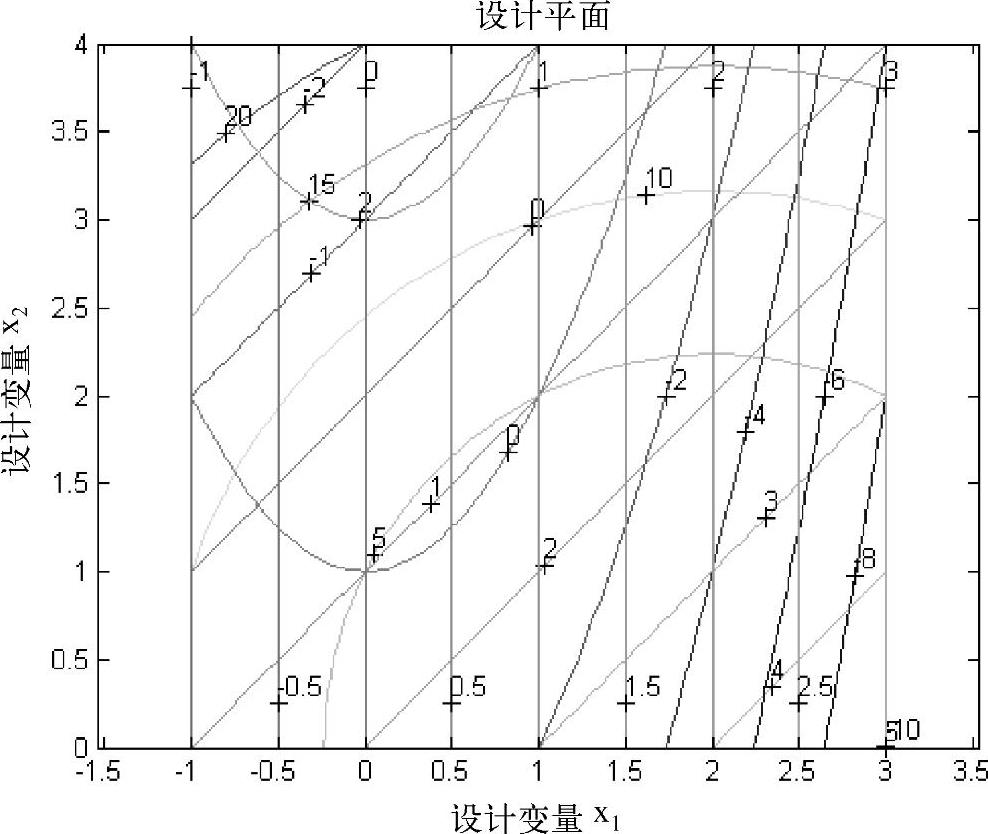
图16-3 二维约束优化问题的设计平面（例16-1）
例16-2 二维非线性约束优化问题（如图16-4所示）
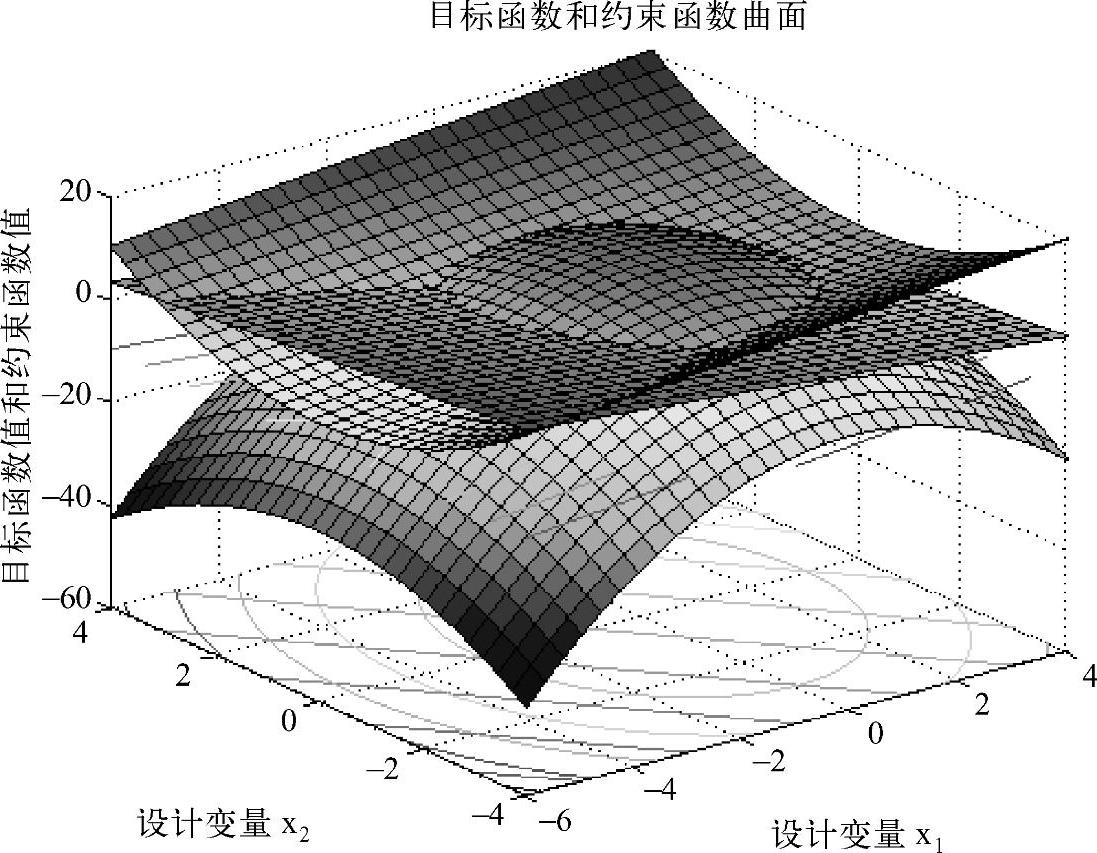
图16-4 二维约束优化问题的目标函数和约束函数曲面组合（例16-2）
如图16-5所示，目标函数f(X)等值线是以x1，轴为对称轴的抛物线族。约束函数g1(X)=0的线图是以(0，0)为圆心、半径为3的圆，约束函数g2(X)=0的线图是通过点(0，1)和点(1，0)的直线。约束极小点是X*=[-3，0]T。
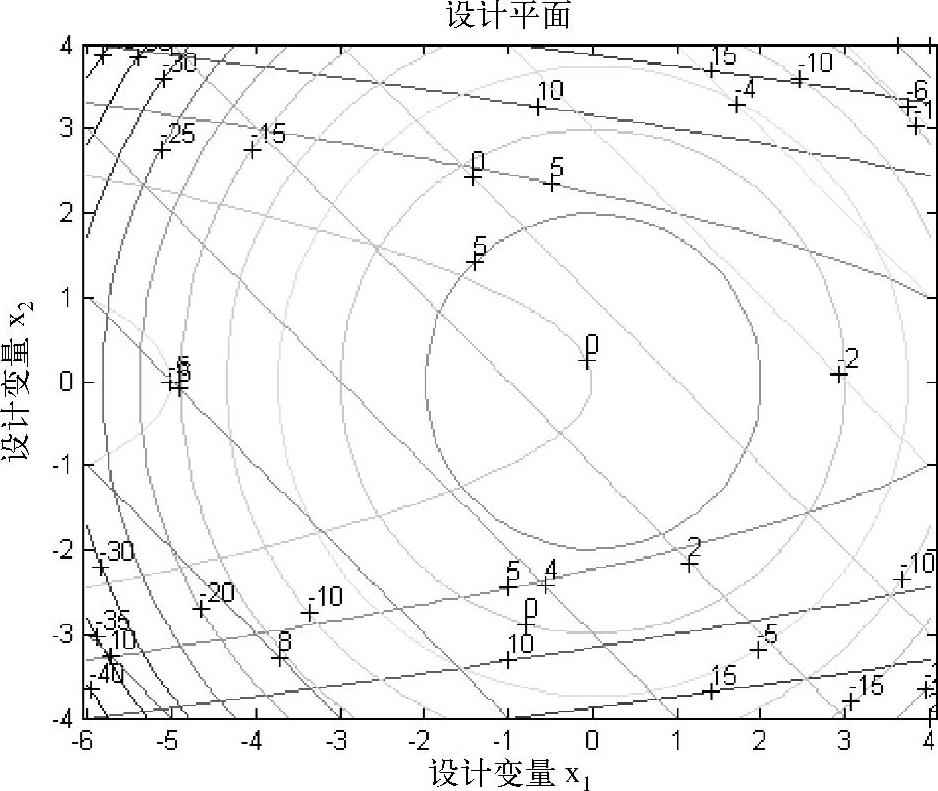
图16-5 二维约束优化问题的设计平面（例16-2）
例16-3 二维非线性无约束优化设计问题
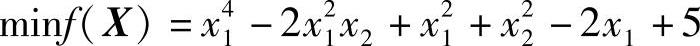
目标函数f（X）曲面、二维等值线和三维等值线如图16-6、图16-7和图16-8所示。
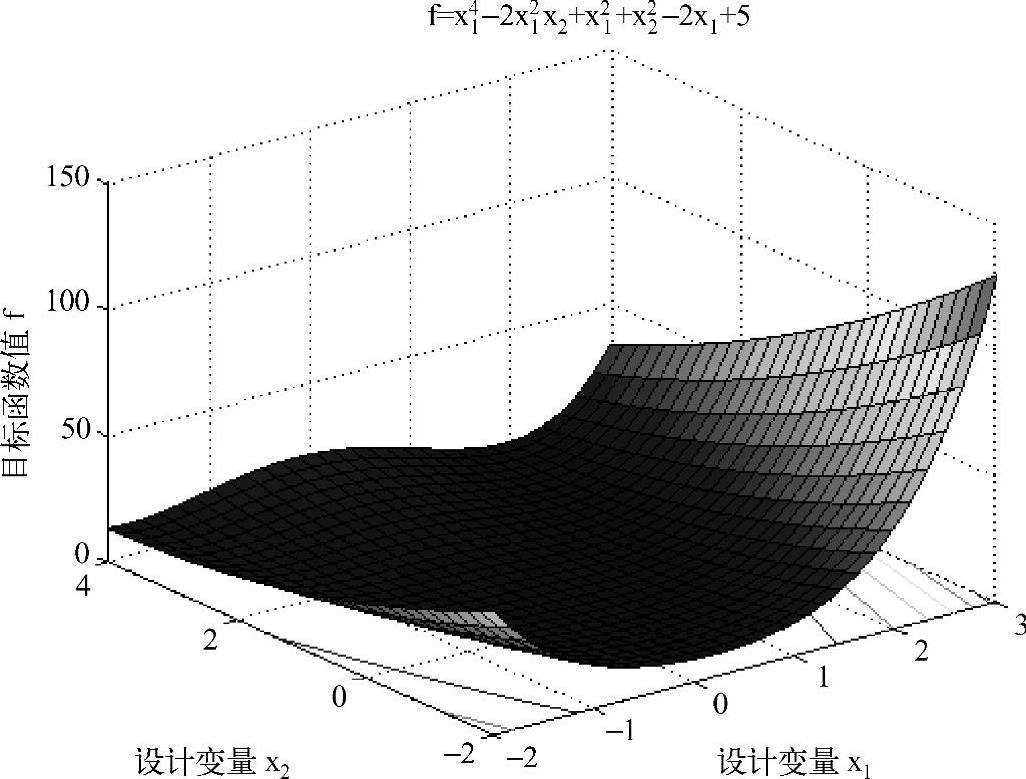
图16-6 二维优化问题的目标函数（例16-3）
例16-4 二维非线性无约束优化设计问题
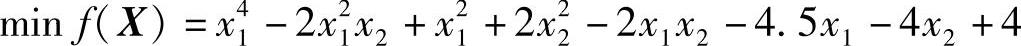(www.xing528.com)
目标函数f（X）曲面、二维等值线和三维等值线如图16-9、图16-10和图16-11所示。
图16-1～16-3，以及图16-4和16-5，分别对二维约束优化问题例16-1和例16-2进行了几何描述；图16-6～16-8，以及图16-9～16-11，分别对两个二维无约束优化问题进行了几何描述。
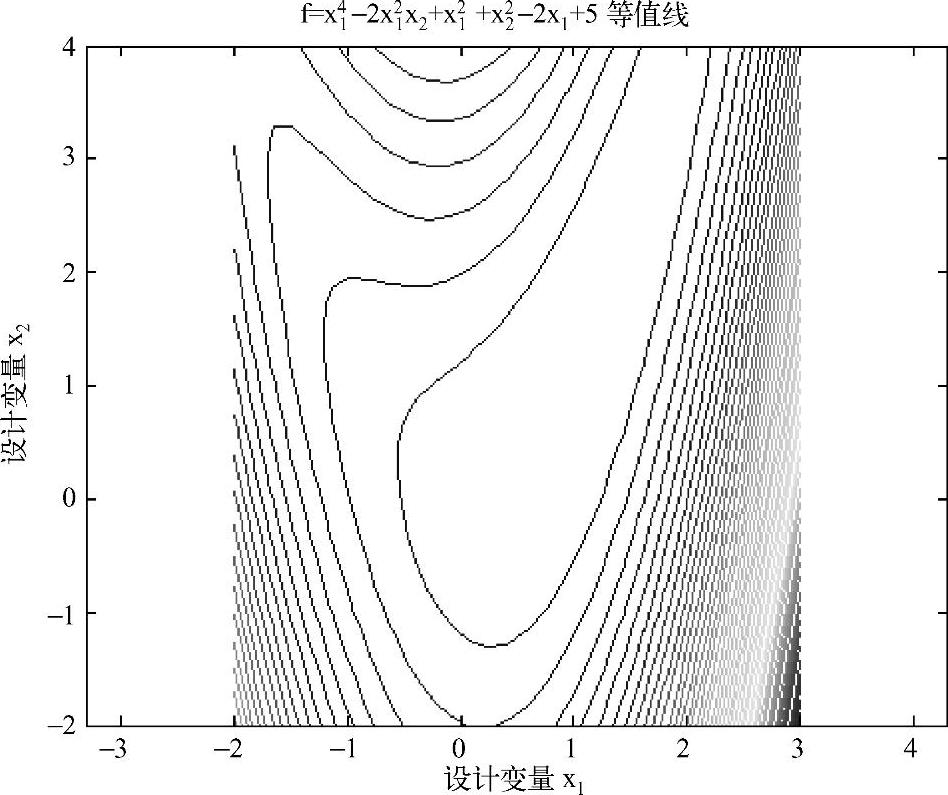
图16-7 二维优化问题目标函数的二维等值线（例16-3）
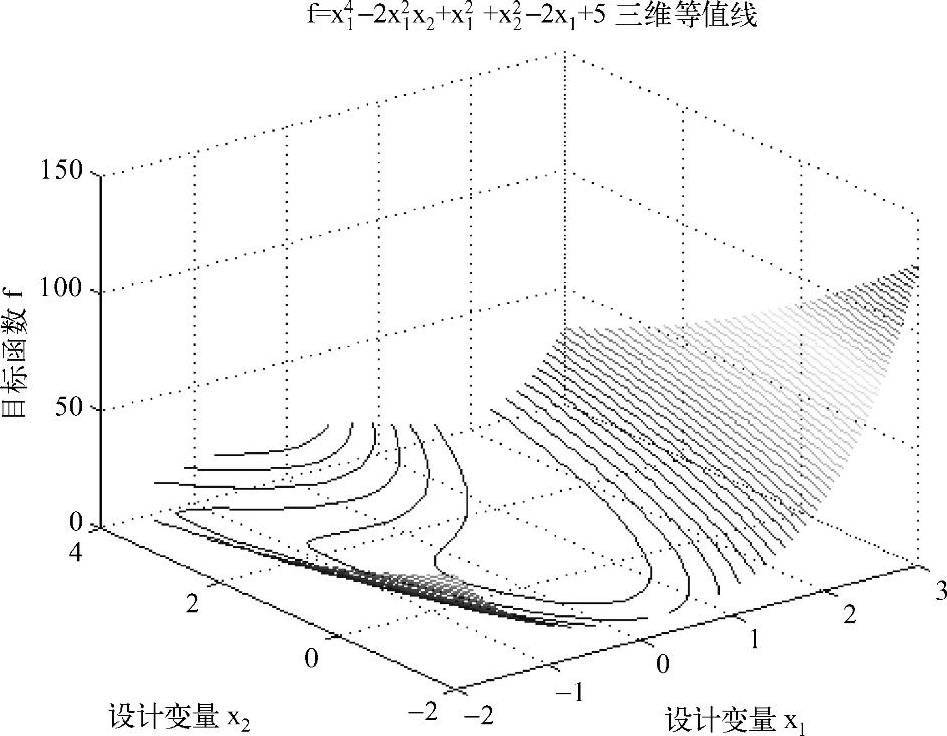
图16-8 二维优化问题目标函数的三维等值线（例16-3）
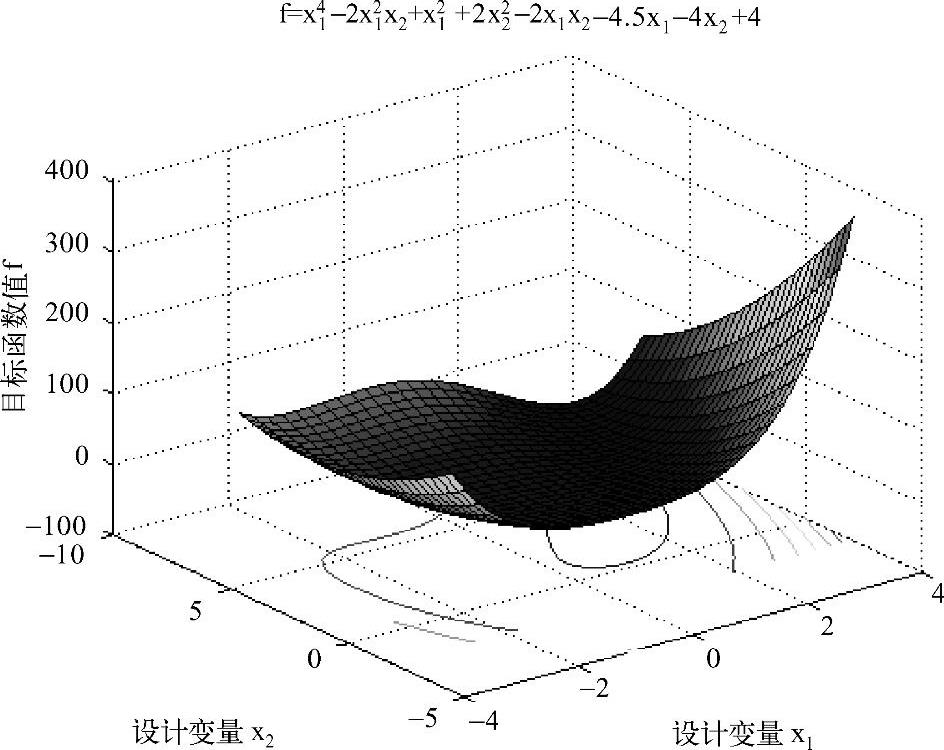
图16-9 二维优化问题的目标函数（例16-4）
从MATLAB绘制f（X）等值线的形状及其分布规律可见，当f（X）是一个二维高次非线性函数时，其等值线的形态比较复杂，而且可能存在多个极值点。在等值线较稠密的部位，f（X）值变化越迅速。对于求f（X）极小化问题来说，越靠近极值点的等值线所代表的f（X）值越小；在极值点附近的等值线呈现椭圆形状，其中心就是极值点X*。
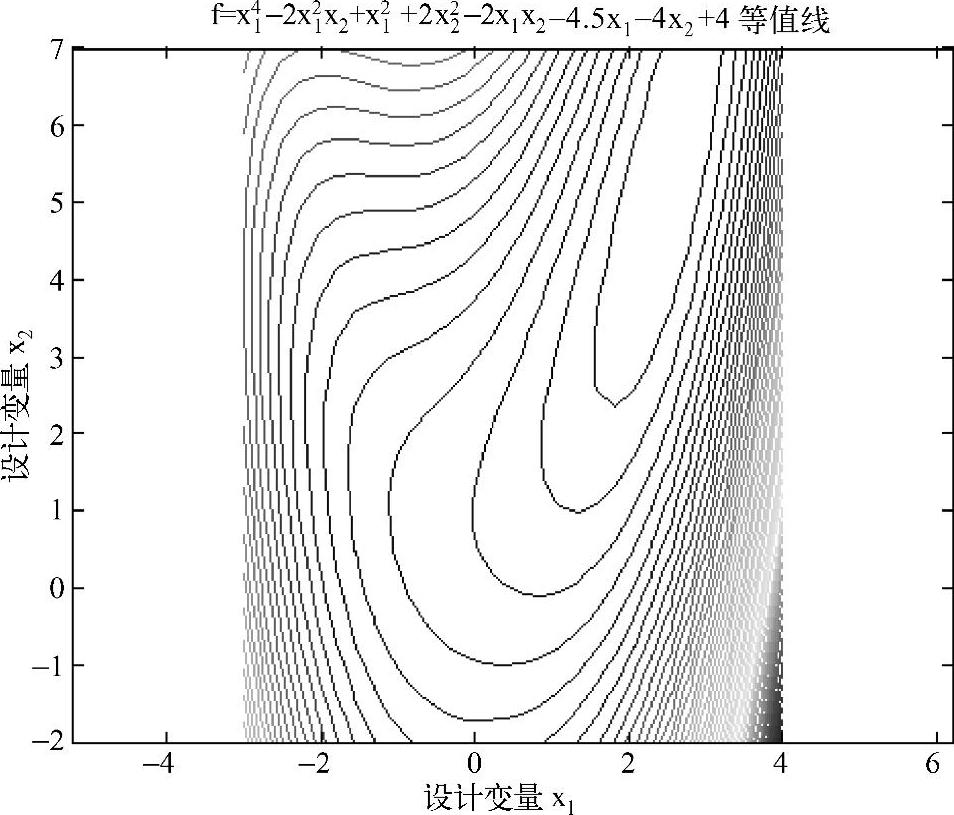
图16-10 二维优化问题目标函数的二维等值线（例16-4）
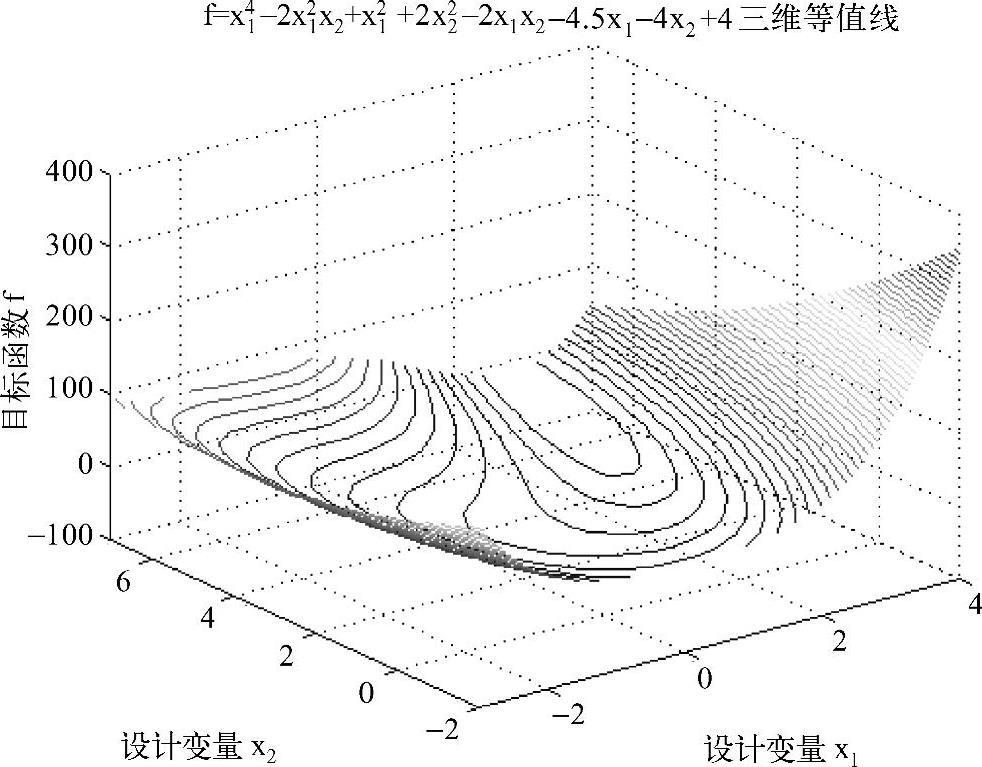
图16-11 二维优化问题目标函数的三维等值线（例16-4）
如图16-6～图16-11所示，由于目标函数f（X）在极值点X*附近的形态比较平缓，造成该区域的等值线分布较稀疏，极值点X*的位置不是十分明显。
应当指出，在MATLAB图形处理中的颜色映像本质上是一个数值矩阵。当在曲面图或等高线图中加入表现颜色的输入参数矩阵时，就可以利用色彩表现或加强目标函数的某些特征，如函数的梯度和方向导数等，直观地了解目标函数在不同方向的变化规律和最快上升或下降方向等特性。
编制二维优化问题几何描述的M文件如下：
例16-1的M文件运行结果如图16-1、图16-2和图16-3所示。
借助MATLAB中强大的绘图功能，以矢量或矩阵作为输入参数，可以直观地描述二维优化设计数学模型的几何形态，作为理解扩展到n维设计空间中复杂超曲面的优化问题的基础。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
