转轴可靠性设计方案优化

例14-5 某圆锥齿轮简支轴危险截面上的弯矩M=10455N．m，转矩T=7903N．m，应力集中源有键槽、圆角和过盈配合。要求转轴运转10⁷次后可靠度R≥0.999，试设计该轴。

1.确定危险截面上的应力分布

1)最大正应力幅s_a的均值（弯曲应力是对称循环，其平均应力为零）

式中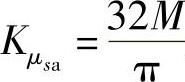，是正应力幅均值系数；μ_d是轴危险截面直径d的均值。

最大正应力幅s_a的标准偏差

式中，v_s是应力的变异系数，根据经验取v_s=0.04～0.08，一般为安全起见，取较大值；K_σsa=v_sK_μsa是正应力幅标准偏差系数。

2）最大平均切应力s_m的均值（扭转切应力是稳定应力，按照第四强度理论）

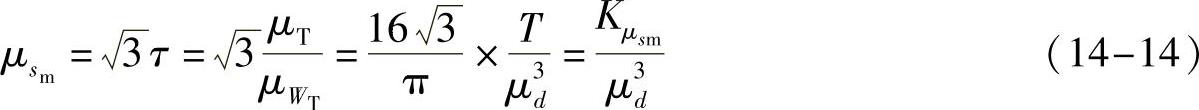
式中，K_μsm=163T/π是切应力均值系数。

平均切应力s_m的标准偏差

式中，Kσ_sm=v_sK_μsm是平均切应力标准偏差系数。

3）应力比均值

4）弯曲和扭转复合疲劳应力s_f的均值

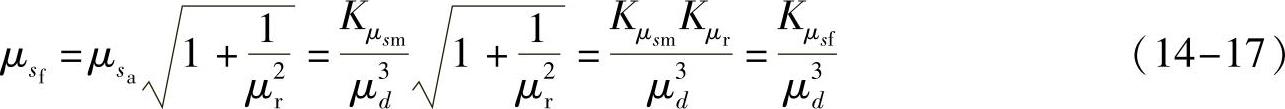
式中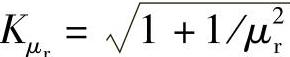，是应力比均值系数；K_μsf=K_μsmK_μr是复合疲劳应力均值系数。复合疲劳应力s_f的标准偏差

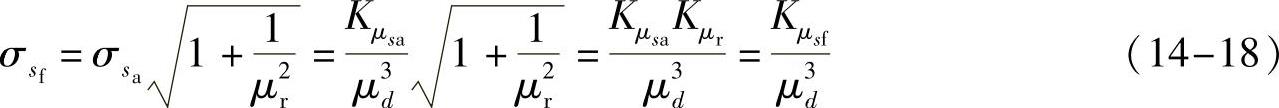
式中，K_μsf=K_μsaK_μr是复合疲劳应力标准偏差系数。

2.确定转轴的强度分布

转轴材料30CrMnTi，硬度>270HBW，强度极限σ_b=950MPa，持久极限σ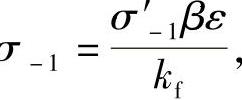其中:

1)试件弯曲持久极限。

2)表面质量系数，当加工表面粗糙度R，，=0.4和强度极限。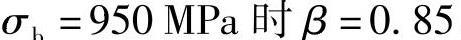

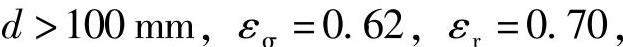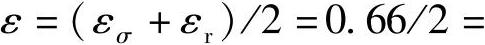3)尺寸系数，当合金钢则0.33。

4)疲劳应力集中系数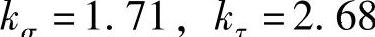，，敏感系数q=0.7437，则(www.xing528.com)

因此，转轴的持久极限

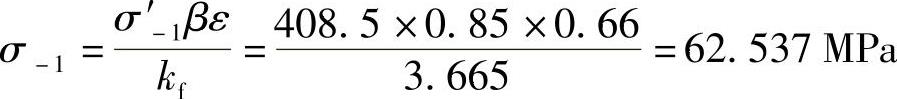
在弯曲和扭转复合疲劳应力下，零件的强度均值按照应力线与最佳拟合线均值的交点求得。强度均值近似为

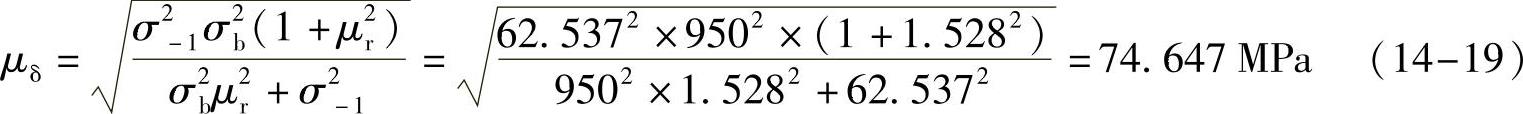
呈现正态分布的古德曼线图中，复合疲劳应力下零件强度的标准偏差

σ_δ=v_δμδ=（0.04～0.08）μ_δ=0.08×74.647=5.974MPa （14-20）

式中，v_δ是强度的变异系数，根据经验取v_δ=0.04～0.08，一般为安全起见，取较大值。

3.确定转轴直径

根据需要的可靠度R，使用MATLAB正态累积分布反函数norminv计算出对应的正态分布变量（联结系数）z值。将有关数据代入联结方程，经过整理得到六次多项式方程

A_μ⁶d+Bμ³_d+C=0 （14-21）

其中，各项系数为

调用MATLAB函数roots求解多项式的根，得到计算结果见表14-6。

表14-6 不同可靠度时的计算结果

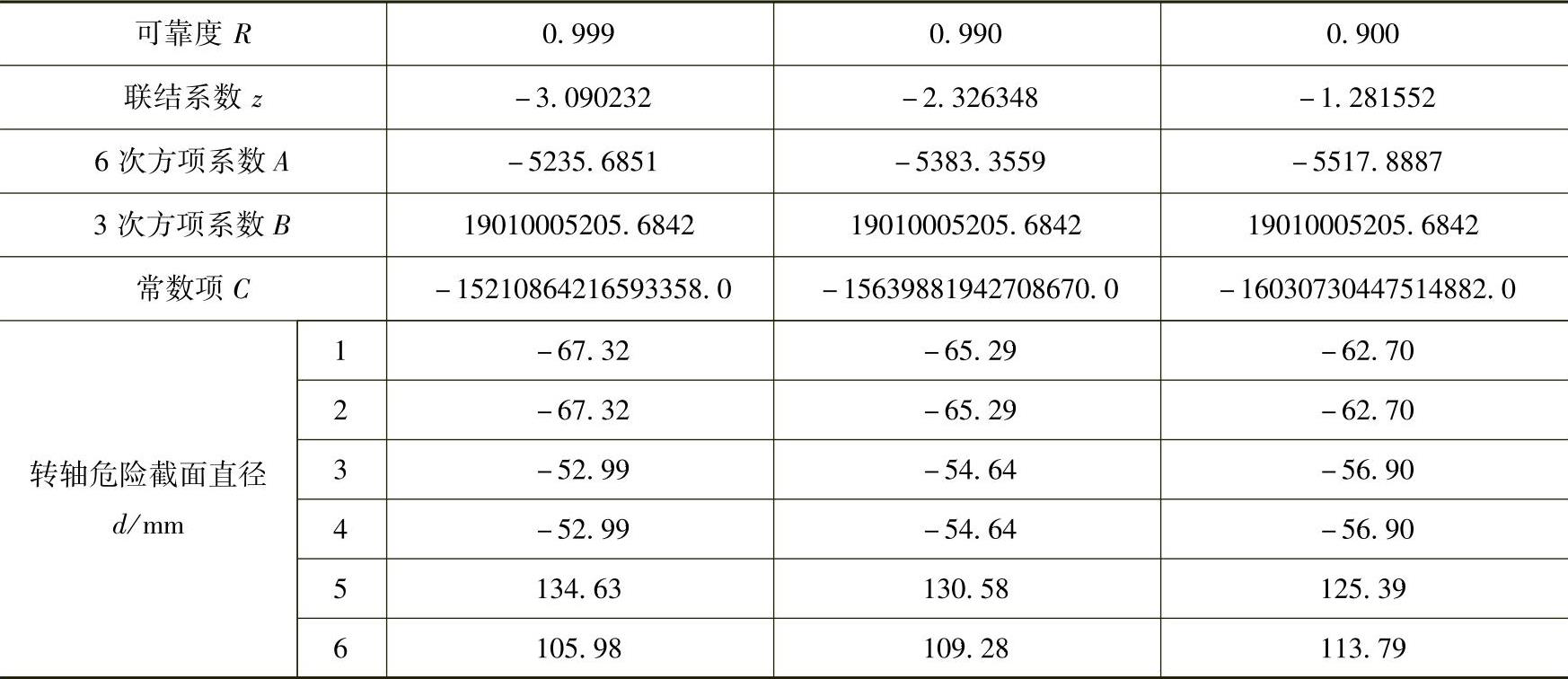
由于六次多项式方程(14-21)是一个齐次方程，所以表14-6中所列的根有两对是相同的负根，它们不符合实际，应该舍去。在其余两个正根中选择较小的作为方程的解。

计算过程使用的中间系数名称，及其计算公式、影响参数和功用见表14-7。

由于转轴危险截面采用花键联接，其小径是106mm>μ_d=105.98mm，所以该转轴危险截面尺寸满足可靠度R=0.999的要求。

表14-7 可靠性计算中的有关系数

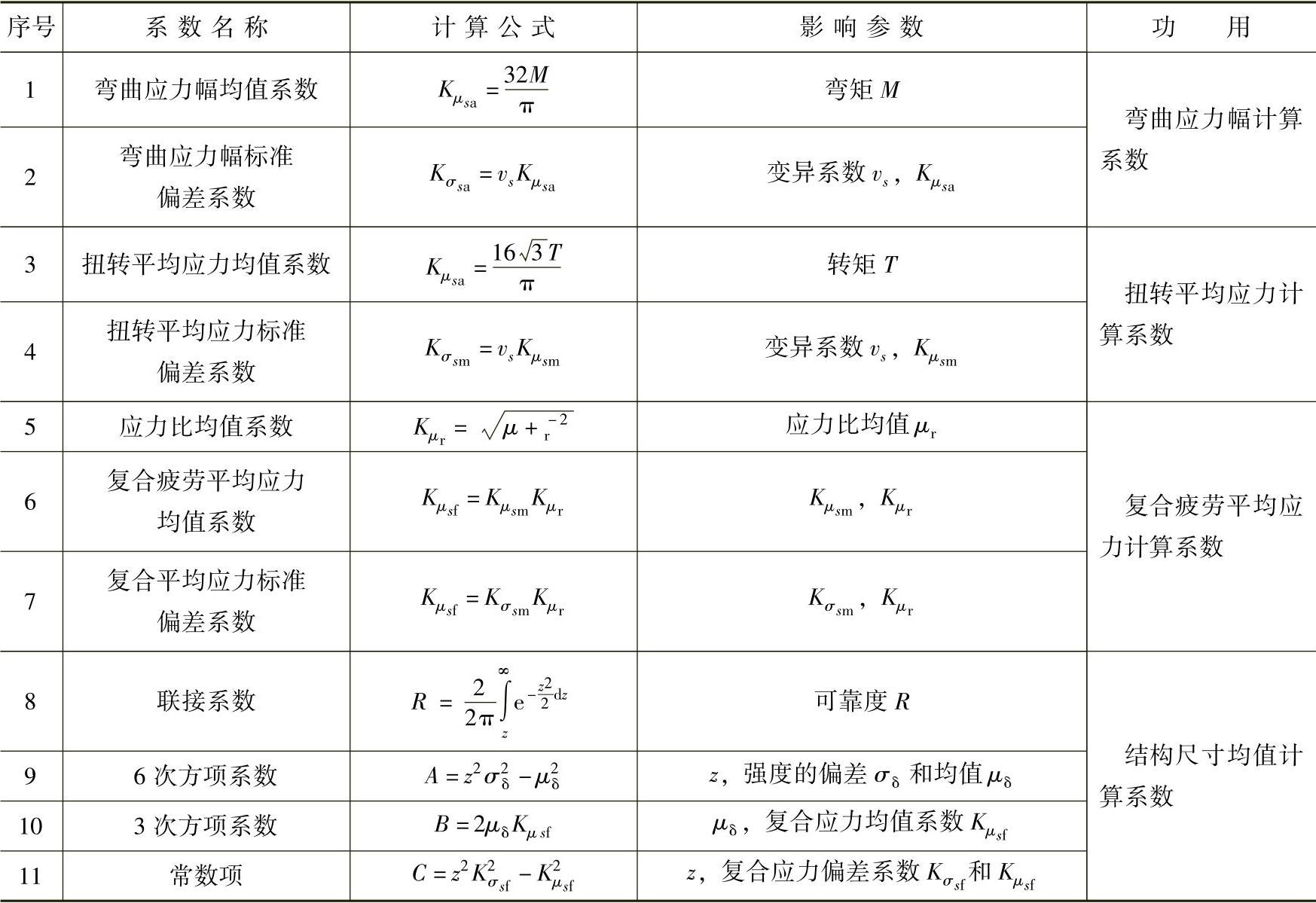
由此可见，在转轴的可靠性设计中，强度分布的均值μ_δ最为重要，对联接方程中的可靠性指数z值有决定性的影响，从而对可靠度R（t）值有决定性的影响。而且，若各种因素致强度分布的标准偏差σ_δ加大，造成机械零件（系统）的可靠度降低，则要求的转轴危险截面直径增大。

综上所述，机械可靠性设计和MATLAB实现的主要步骤是：

1）计算转轴危险截面上复合疲劳应力分布的平均应力系数和标准偏差系数。

2）计算转轴危险截面上强度分布的强度均值和强度标准偏差。

3）使用联接方程计算危险截面轴径，其中主要内容是：根据可靠度R用正态累积分布反函数norminv（1-R）确定联接系数z；根据联接系数z用正态累积分布函数normcdf（z）确定失效概率F；用正态分布概率密度函数normpdf（z）确定失效频度f；根据多项式各次项系数向量P用求解多项式根的函数roots（P）计算转轴直径d。