实例计算与M文件编写：一一学习使用方法

例14-3 已知某轴承环卡盘多刀车床主轴采用上述支承结构（图14-3），前支承上安装一对圆锥滚子轴承（Y=1.5）。主轴组件的结构尺寸为：l=525mm、a=203mm、b=130mm、c=194mm。轴头处安装斜齿轮分度圆直径d=271.31mm，车床经济切削直径D=180mm。齿轮传动力Q_t=4839N、Q_r=1820N、Q_a=1294N，载荷方位角φ=128°。切削力P_z=6978N、P_y=2971N、P_x=2791N。试求主轴前支承的径向反力F_r。

（1）计算主轴轴向力

F_a=P_x^-Qa=2791-1294=1497N（方向向左）因此，前支承的径向反力F_r的作用位置偏向于前支承对称平面的右边（图14-9）。

（2）由式（14-5）求出力矩参数（略去具体计算过程）

u=-393536N·mm

v=-5453056N·mm

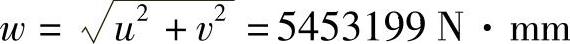
（3）由式（14-7）求出相对位置系数

因此，根据式(14-6)求出主轴前支承的径向反力F_r=10384N，作用位置b₁=22.12mm。

同理，分别根据水平面XOY中y方向上和垂直面XOZ中Z方向上力系的平衡条件，计算出主轴后支承的径向反力F_rA=2644N。

讨论：如果由于T作条件改变，切削轴向力变成P_x=4400N，其他数据不变。则主轴轴向力变成F_a=3106N（方向向左）。P_x值的改变不会引起υ值的变化。

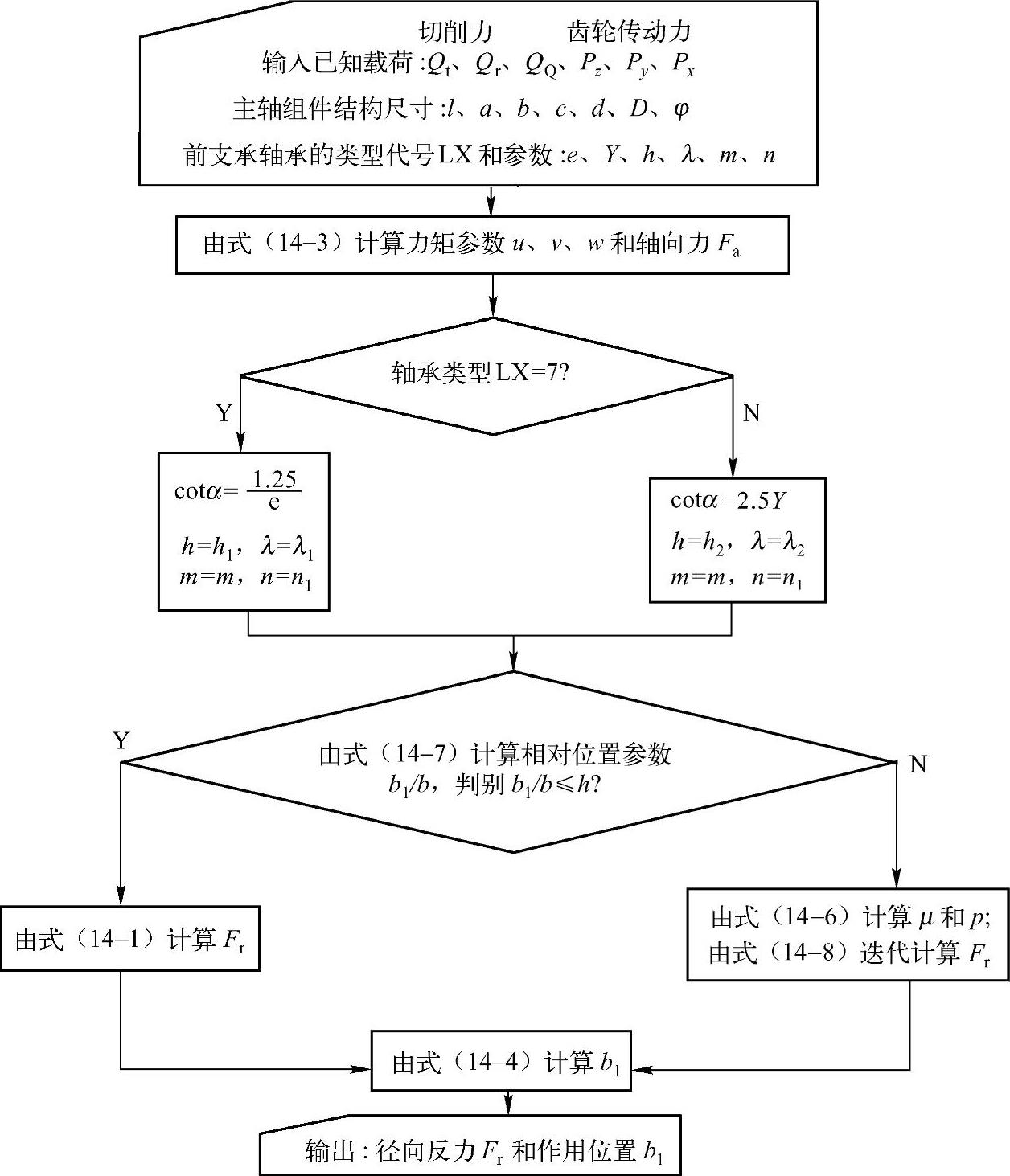
图14-10 主轴静不定结构计算流程图(www.xing528.com)

u=105274N·mm

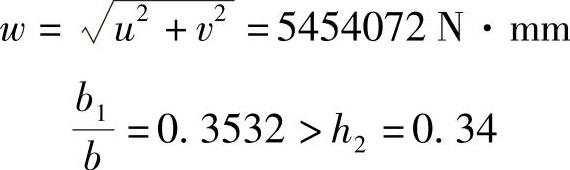
由式（14-8）求出μ=61051，ρ=15.7101。

（4）M文件和运算结果 选择MATLAB中函数fsolve，求解非线性超越方程式（14-9）。使用时，取迭代初值

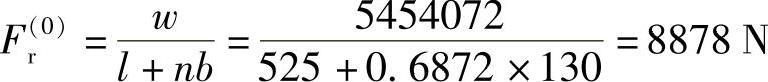
在zzjbd.m函数文件中定义方程式（14-9）的函数表达式，并且使用函数global将主M文件中的输出变量μ和ρ定义为全局变量，以便函数表达式中使用。

计算结果：