螺旋传动设计计算的主要内容

普通滑动螺旋传动设计计算的主要内容是：耐磨性计算、螺杆的强度计算、螺母螺纹牙的强度计算、自锁条件计算和螺杆的稳定性计算等。

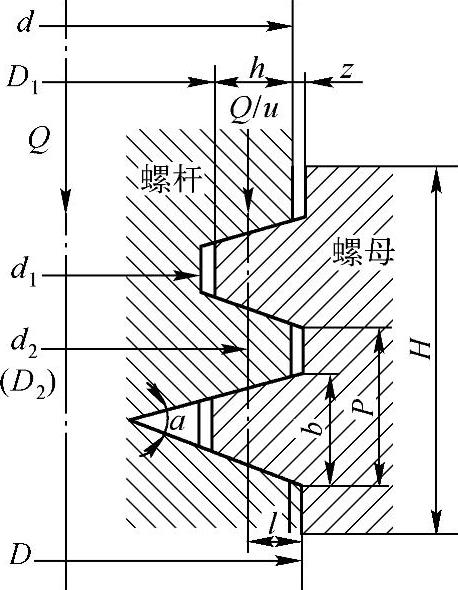
图13-7 螺旋传动参数尺寸和受力分析

1.耐磨性计算

滑动螺旋的磨损与螺纹工作面上的压力、滑动速度、螺纹表面粗糙度以及润滑状态等因素有关。其中最主要的是螺纹工作面上的压力，压力越大螺旋副间越容易形成过度磨损。因此，滑动螺旋的耐磨性计算，主要是限制螺纹工作面上的工作应力p小于材料的许用应力[p]。

如图13-7所示，假设作用于螺杆的轴向力为Q（N），螺纹的承压面积（指螺纹工作表面投影到垂直于轴向力的平面上的面积）为A（mm²），螺纹中径为d₂（D₂），螺纹工作高度为h（mm），螺纹螺距为P（mm），螺母高度为H（mm），螺纹工件圈数为u=H/P。则螺纹工作面上的耐磨性条件校核公式

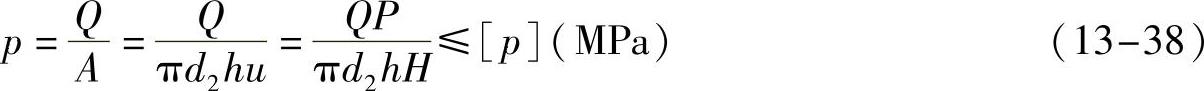
令螺母高度系数φ=H/d₂，一般φ=1.2～3.5。对于整体螺母，由于磨损后不能调整间隙，为使受力分布比较均匀，螺纹工作圈数不宜过多，故取φ=1.2～2.5；对于剖分螺母和兼作支承的螺母，可取φ=2.5～3.5；只有传动精度较高，载荷较大，要求工作寿命较长时，才允许取φ=4。

将螺母高度H=φd₂代入式（13-38）整理后，得到耐磨性条件设计公式

式中，对于矩形和梯形螺纹的螺纹工作高度h=0.5P；[p]是材料的许用应力。

根据式（13-39）算得螺纹中径d₂后，应按国家标准规范选取相应的公称直径d及螺距P。螺纹工作圈数u不宜超过10圈。

2.螺旋副自锁条件计算

螺纹几何参数确定后，对于有自锁性要求的螺旋副，还应校核螺旋副是否满足自锁条件

式中，γ是螺纹导程角；f_v是螺旋副的当量摩擦因数；ρ_v是当量摩擦角；β是螺纹牙型斜角，对于梯形螺纹β=15°，锯齿形螺纹工作面β=15°，非工作面β=1.5°；f是材料摩擦因数。

3.螺杆的强度计算

受力较大的螺杆需进行强度计算。螺杆工作时承受轴向力和转矩的共同作用，根据第四强度理论求出危险截面的组合应力σ_e，其强度条件为

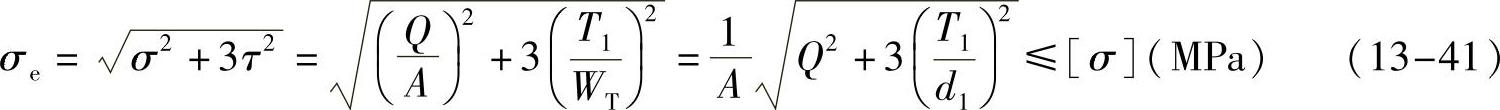
式中，螺杆的螺纹小径d₁，单位为mm；螺纹段危险截面面积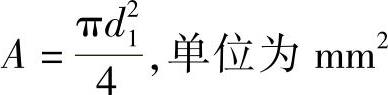；螺纹段抗扭截面系数W_T=πd³₁/16=Ad₁/4，单位为mm³；螺杆所受转矩（即螺旋副的摩擦力矩）T1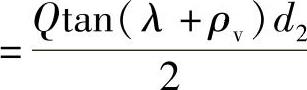，单位为N·mm；螺杆材料的许用应力[σ]，单位为MPa。

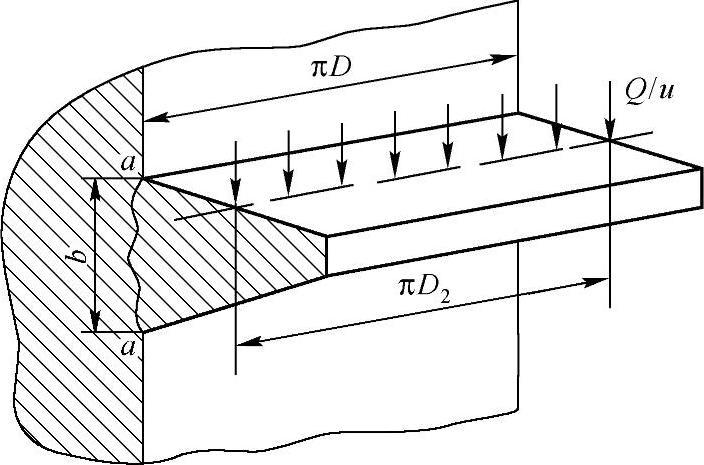
图13-8 螺母螺纹牙的强度计算

4.螺母螺纹牙的强度计算

螺纹牙多发生剪切和挤压破坏，一般螺母的材料强度低于螺杆，故只需校核螺母螺纹牙的强度。

（1）抗剪强度条件 如图13-8所示，如果将一圈螺纹沿螺母的螺纹大径D处展开，则可看作宽度为πD的悬臂梁。假设螺母每圈螺纹所承受的平均压力为Q/u，并作用在以螺纹中径D₂为直径的圆周上，则螺纹牙危险截面a-a的抗剪强度条件为(www.xing528.com)

式中，螺母材料的许用切应力是[τ]。

（2）抗弯强度条件 螺纹牙危险截面a-a的抗弯强度条件为

式中，螺纹牙根部的厚度b，单位为mm，对于矩形螺纹b=0.5P，对于梯形螺纹b=0.65P，对于30°锯齿形螺纹，b=0.75P，P为螺纹螺距；弯曲力臂l=（D-D₂），单位为mm；螺母材料的许用弯曲应力为[σ]_b。

当螺杆和螺母的材料相同（如钢制螺旋副）时，由于螺杆的小径d₁小于螺母螺纹的大径D，故应校核螺杆螺纹牙的强度。此时，式（13-43）中的D应改为d₁。

5.螺杆的稳定性计算

对于长径比大的受压螺杆，当轴向压力Q大于某一临界值时，螺杆就会突然发生侧向弯曲而丧失其稳定性。因此，螺杆承受的轴向力Q必须小于临界载荷Q_c时的稳定性系数即

式中，螺杆稳定性安全系数S_s，对于传力螺旋（如起重螺杆等）S_s=3.5～5.0，对于传导螺旋S_s=2.5～4.0，对于精密螺杆或水平螺杆S_s>4.0。

螺杆的临界载荷Q_c根据螺杆的柔度λ_s值的大小选用不同的公式计算

式中，螺杆长度系数_μ=2.0（对于螺旋起重器的螺杆，可以按照一端固定，一端自由）；L是螺杆的工作长度，单位为mm，若螺杆两端有支承时，取两支点间的距离作为工作长度；若螺杆一端以螺母支承时，则以螺母中部到另一端支点的距离，作为工作长度；i为螺杆危险截面的惯性半径，单位为mm，若螺杆的危险截面面积A=πd²₁，则

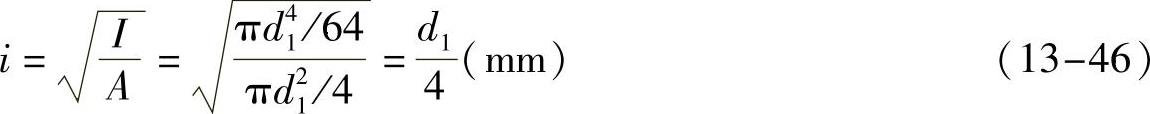
式中，螺杆危险截面的惯性矩I=πd⁴₁/64，单位为mm⁴。

1）螺杆的柔度λ_s≥90时，临界载荷Q_c可按欧拉公式计算

式中，钢制螺杆的拉压弹性模量E=2.06×10⁵MPa。

2）40≤λ_s<90时，对于未淬火钢，取临界载荷

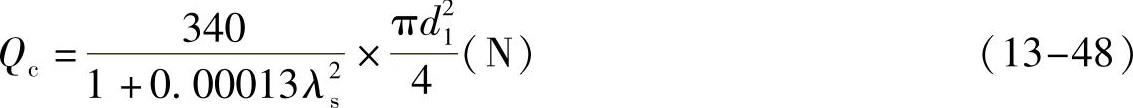
对于淬火钢，取临界载荷

3）λ_s<40时，可以不进行稳定性校核。