建立数学模型进行优化设计

在蜗杆传动中，为了减摩耐磨，通常蜗轮齿圈需用贵重的青铜等材料制造。为了节省较贵重的非铁金属，降低成本，在蜗杆传动的优化设计中，应该以蜗轮非铁金属齿圈体积最小作为设计目标。

1.目标函数和设计变量

如图13-6所示，蜗轮齿圈的结构尺寸包括：齿顶圆直径d_a、齿根圆直径d_f、齿圈外径d_e、内径d₀和齿宽b。蜗轮齿圈的体积可以表示为

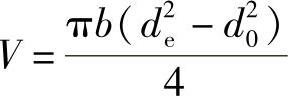
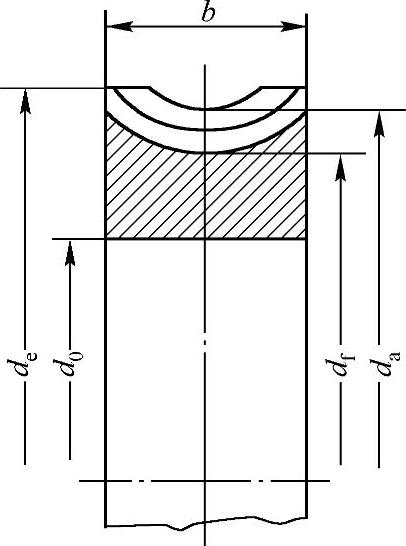
图13-6 蜗轮齿圈的结构尺寸

齿宽b 齿圈外径d_e 齿顶圆直径d_a 齿根圆直径d_f 内径d0

式中，蜗轮齿圈外径d_e和齿宽b，根据蜗杆头数z₁按照表13-2选取。

表13-2 蜗轮齿圈外径d_e和宽度b的选取

从表13-2可知，d_e=d_a+ψ_em，b=ψ_bd_a1，两式中的系数ψ_e和ψ_b根据表13-2确定（根据蜗杆头数z₁不同，ψ_e=2、1.5或1，ψ_b=0.75或0.67）。

● 齿圈内径d₀=d_f-2m。

● 蜗杆齿顶圆直径d_a1=（q+2）m，q是蜗杆的直径系数。

● 蜗轮齿数z₂=iz₁，其中i是传动比；z₁是蜗杆头数。

● 蜗轮齿顶圆直径d_a=（z₂+2）m=（iz₁+2）m。

● 蜗轮齿根圆直径d_f=（z₂-2.4）m=（iz₁-2.4）m。

将上述关系代入蜗轮齿圈的体积计算式得到

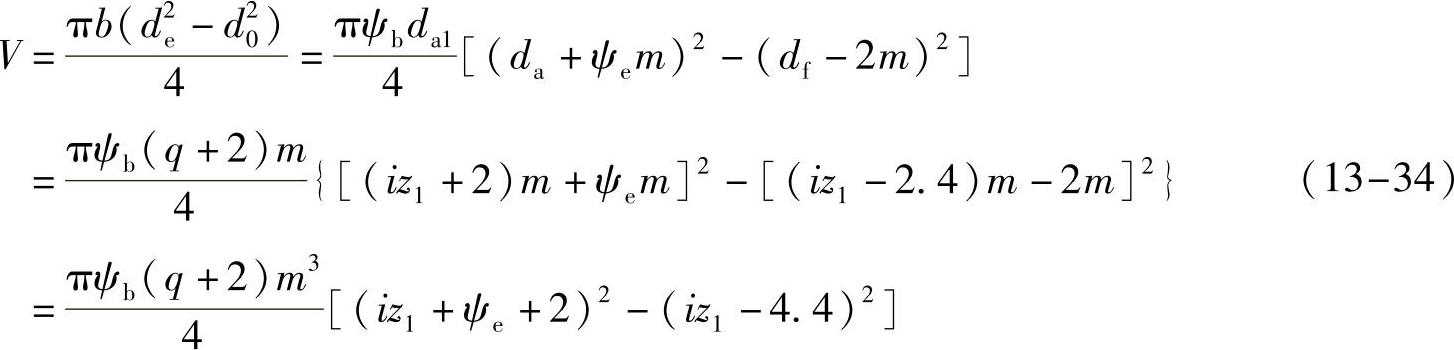
从式（13-34）可知，除了系数ψ_e和ψ_b根据从表13-2确定外，蜗轮齿圈的体积是蜗杆头数z₁、模数m、直径系数q和传动比i的函数。由于传动比i一般是已知量，因此，取蜗杆头数z₁、模数m和直径系数q作为设计变量，即

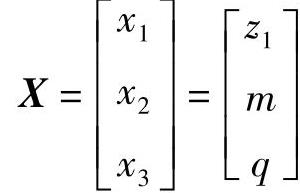
因此，根据式（13-34）可以将目标函数写成

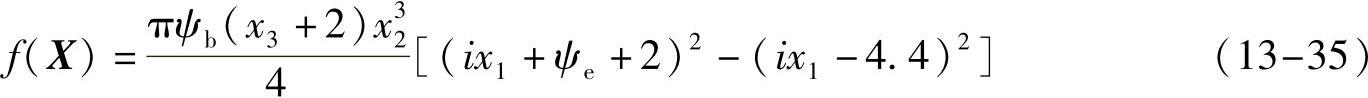
2.约束条件

1）蜗轮齿面接触强度的限制：根据蜗轮齿面接触强度条件(www.xing528.com)

式中，载荷系数K=1~1.4，载荷平稳，齿面滑动速度≤3m/s．7级以上精度时取小值：蜗轮传递的转矩

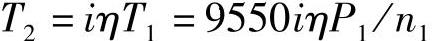
蜗杆传动效率

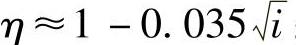
[σ_h]是蜗轮齿圈材料的许用接触应力。

因此得到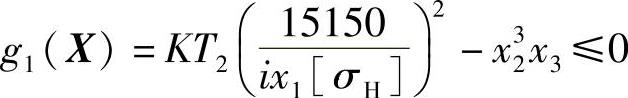

2）蜗轮齿根弯曲强度的限制：由于蜗轮轮齿的齿根是圆弧形，抗弯能力较高，很少发生蜗轮轮齿折断。所以，对于闭式蜗杆传动，通常不再进行蜗轮齿根弯曲强度计算。

3）蜗杆刚度的限制：要求蜗杆工作时最大挠度不大于0.001d₁=0.001mq，即

式中，蜗杆支承跨度L≈0.9d₂=0.9miz₁；惯性矩J=π/64d⁴_f1=π/64m⁴（q-2.4）4；蜗杆圆周力F_t1=2T₁/d₁=2T₁/mq；径向力F_r1=2T₂tan20°/d₂=2T₂tan20°/iz₁m；弹性模量E=2.1×10⁵MPa（钢）。将上述关系代入式（13-37）整理得到

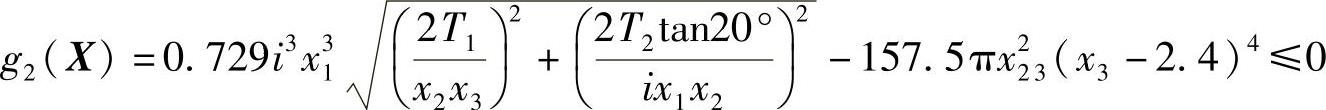
4）蜗杆头数的限制：对于动力传动，要求z₁=2～4。因此有

g₃（X）=x₁-3≤0

g₄（X）=2-x₁≤0

5）模数的限制：对于中小功率的蜗杆动力传动，要求3≤m≤5。因此有

g₅（X）=x₂-5≥0

g₆（X）=3-x₂≤0

6）蜗杆直径系数的限制：对应上述模数的范围，要求5≤q≤16。因此有

g₇（X）=x₃-16≤0

g₈（X）=5-x₃≤0

综上所述，优化设计数学模型是有6个边界约束和2个性能约束的3维非线性规划问题。