螺旋齿轮传动的工作原理

1.齿轮副的轴夹角

如图13-4a所示的螺旋齿轮传动，两轮分度圆相切于C点，两轮轴线在两轮分度圆柱公切面上投影的夹角，称为两轮的轴夹角，其值为

∑=β₁±β₂ （13-29）

式中，β₁与β₂分别是两轮的螺旋角；“+”号用于两轮螺旋角方向相同时，“-”号用于两轮螺旋角方向相反时。若∑=0，β₁=-β₂，则为平行轴外啮合斜齿圆柱齿轮机构。

与平行轴斜齿轮传动不同的是，由于交错轴斜齿轮副的两轮螺旋角不一定相同，因此两轮的端面模数和端面压力角也不一定分别相等。

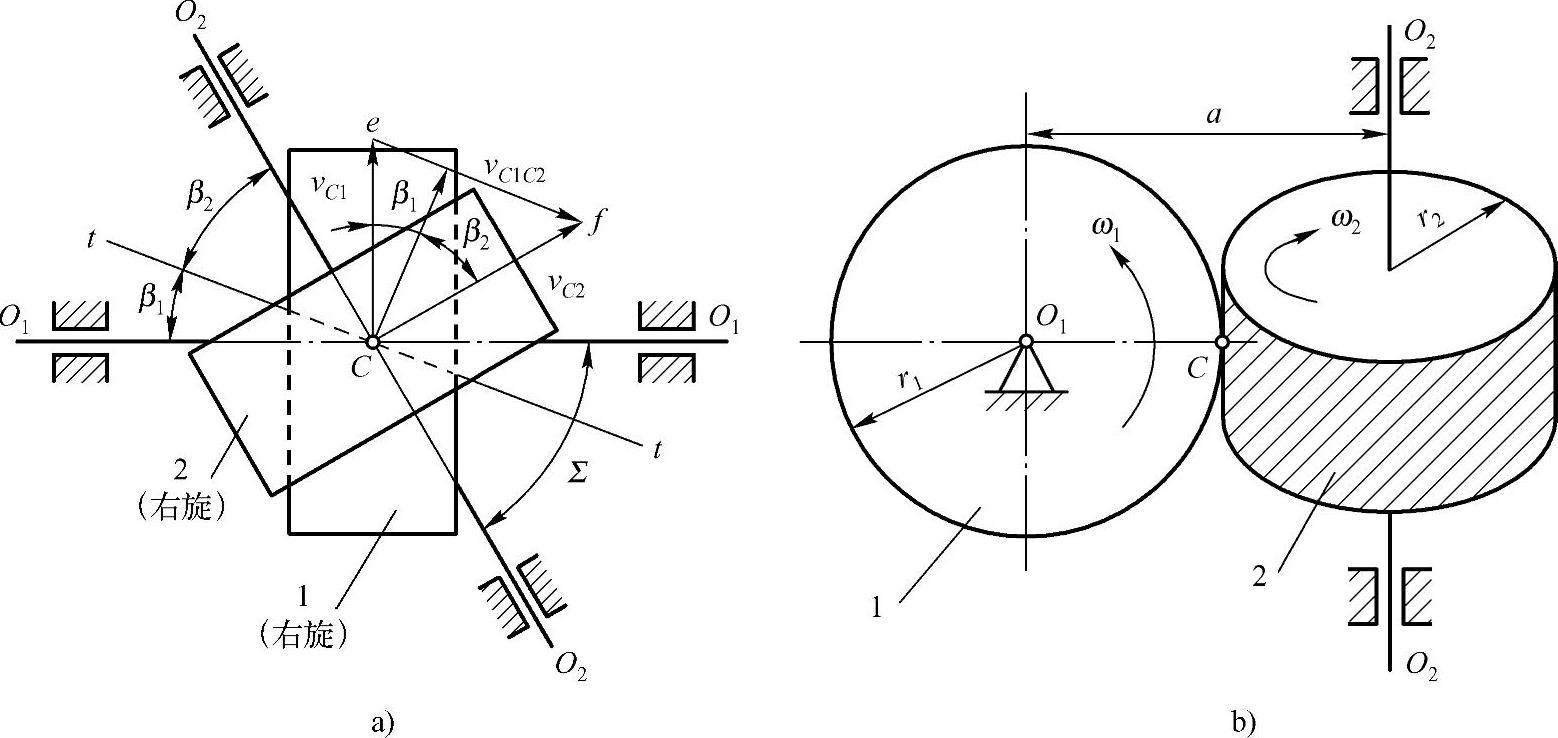
图13-4 螺旋齿轮传动

2.中心距

如图13-4b所示，过C点作交错轴斜齿轮副轴线的公垂线，它的长度就是交错轴斜齿轮传动的中心距

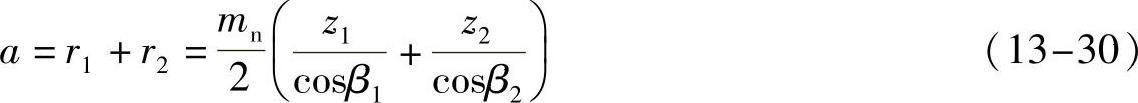
3.传动比

假设两轮的端面模数分别为m_t1与m_t2，分度圆直径分别为d₁与d₂，则两轮齿数分别为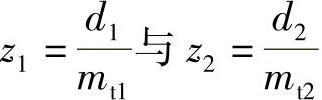。因此，两轮的传动比为

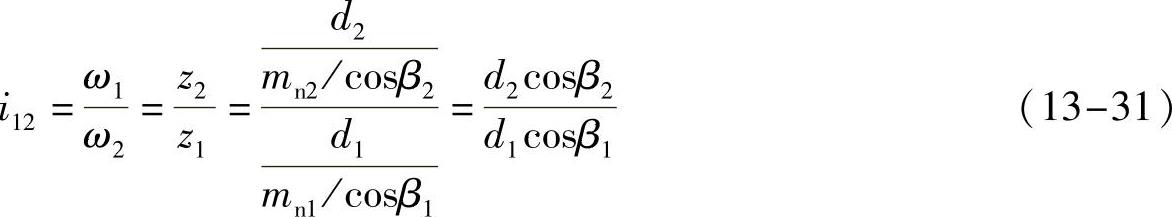(www.xing528.com)

螺旋齿轮的传动比i是恒定的，两轮的中心距a或轴夹角∑改变时，传动比不受影响。

4.常规啮合的无侧隙啮合方程式

螺旋齿轮常规啮合（最紧密啮合）时的中心距最小，重合度最大，这时无侧隙啮合方程式为

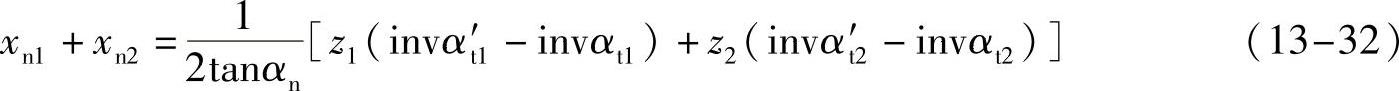
式中，x_n1与x_n2分别是两轮的法面变位系数；α_t′₁与α_t1分别是齿轮1的端面啮合角和端面压力角；α′_t2与α_t2分别是斜齿轮2的端面啮合角和端面压力角；z₁与z₂分别是两轮的齿数。

5.齿轮副的实际啮合线

螺旋齿轮副的实际啮合线长度为

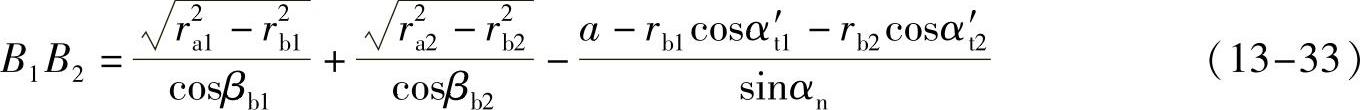
式中，r_a1与r_a2分别是两轮的齿顶圆半径；r_b1与r_b2分别是两轮的基圆半径；α_t′₁与α_t′₂分别是两轮的端面啮合角；β_b1与β_b2分别是两轮的基圆螺旋角；α_n是齿轮的法面压力角；a是齿轮副中心距。

6.从动轮的转向

交错轴斜齿轮传动中从动轮的转向取决于两齿轮螺旋角的大小和方向，它可以通过速度矢量图解法来确定。例如，在图13-4a中，假设齿轮1是主动轮，它在节点C处的速度υ_C1方向是已知的（与齿轮1的轴线O₁O₁垂直），两齿轮在节点C的相对滑动速度υ_C1C2方向ef应该与两齿轮齿面在节点C处的公切线tt平行；斜齿轮2的速度方向应该与斜齿轮2的轴线O₂O₂垂直，作出速度矢量△Cef的封闭边Cf，它就是斜齿轮2在节点C的速度矢量υ_C2。因此，从动轮的转向如图13-4b所示。

综上所述，交错轴斜齿轮传动的特点是，可以通过改变两齿轮螺旋角的大小来调整两齿轮的轴夹角、中心距和传动比[式（13-29）～式（13-31）]，或通过改变两齿轮螺旋角的方向来调整从动轮的转向。交错轴斜齿轮传动的主要缺点是相互啮合的齿廓为点接触，而且齿廓之间除了沿齿高方向有相对滑动外，沿螺旋齿槽方向也有较大的相对滑动，造成齿廓磨损快，传动效率低，一般适用于低速轻载的辅助传动中。