测定和计算变位齿轮传动参数

1.确定齿轮的模数和齿制参数

通过测量齿顶圆和齿根圆直径，确定模数m和齿制参数h_a^*、c^*。图13-1a、b所示分别为偶数齿和奇数齿的齿顶圆和齿根圆直径的测量。显然对于奇数齿齿轮

d_a=D+2H₁

d_f=D+2H₂

因此，齿高

齿轮模数

将两种齿制参数：正常齿h_a^*=1.0、c^*=0.25和短齿h_a^*=0.8、c^*=0.30代入式（13-2）进行计算，得到的模数接近标准值的即为齿轮的实际模数m（取标准值）。

2．确定齿轮的压力角和变位系数

通过测量公法线长度确定压力角α和变位系数x。跨齿数

计算的跨齿数四舍五入取整。

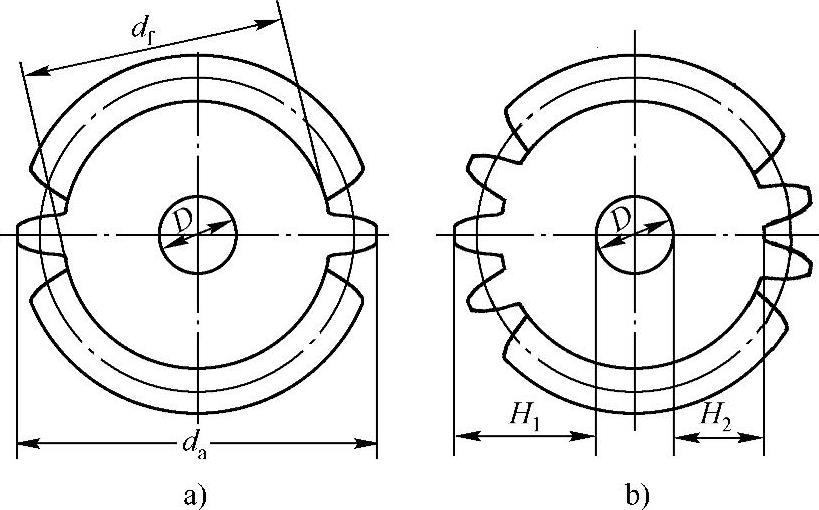
图13-1 齿根圆和齿顶圆直径的测量

分别测量跨k个齿的公法线长度W_k′和跨k+1个齿的公法线长度W_k′₊₁，则压力角

将计算得到的压力角α圆整为接近的标准值20°或15°。公法线长度的测量如图13-2所示。

(www.xing528.com)

图13-2 公法线长度的测量

变位系数

式中，标准齿轮公法线长度为

W_k=mcosα[（k-0.5）π+z×invα] （13-6）

3.确定齿轮副的啮合角和实际中心距

确定齿轮副的变位系数x₁和x₂后，根据无侧隙啮合方程式计算啮合角

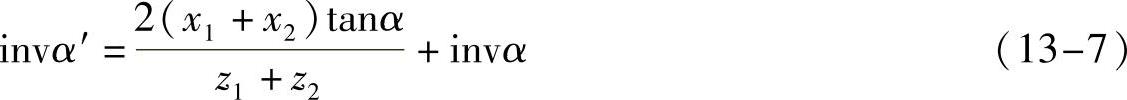
式中，等号右边都是已知数据（下式中用“xzα”表示），利用MATLAB中的fsolve函数求解该非线性方程f（α′）=tanα′-α′-xzα=0，即得到啮合角α′。实际中心距

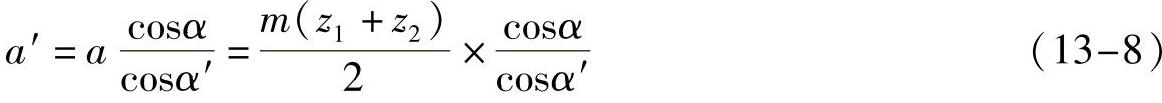
4.计算实例的M文件和运算结果

例13-1 测定变位直齿圆柱齿轮的齿数z=8，齿根圆直径d_f0=33.43mm，公法线长度W₂=24.73和W₃=39.43，试确定齿轮的其他基本参数。

计算结果：

齿顶高系数与顶隙系数之和 hc=1.25