凸轮机构运动参数分析

（1）凸轮角速度ω1

（2）转盘分度数I（转盘每转一周中的停歇次数） 对于如图11-8所示的双头型（凸轮头数H=2）共轭平面分度凸轮机构，转盘分度数通常可取3、4、5、6、8（按照工作机械要求的工位数选取）。

（3）凸轮头数H 通常可取1、2、3、4，头数少的凸轮形状比较简单，但是受到凸轮轮廓的组合条件、压力角条件和不根切条件等限制时，可以取凸轮头数H=3或4。

（4）转盘滚子数z（包括转盘的前后两个端面上的滚子）

z=HI （11-8）

（5）凸轮分度期转角θ_f和停歇期转角θ_d 对于双头型共轭平面分度凸轮机构的凸轮，分度期转角通常可取θ_f=90°～270°（间隔为30°）。凸轮停歇期转角

（6）转盘分度期转位角φf

（7）转盘分度期运动规律 普通的正弦运动规律的始、末区段，从动件运动速度变化相当缓慢，导致中间区段的类速度幅度偏大。为改善这种情况，在始、末区段采用与中间区段不同周期的正弦运动规律（凸轮始、末区段对应的凸轮转角各占整个转角的1/8），即改进的正弦运动规律——组合摆线运动规律，如图11-9所示。它适用于中高速重载荷。

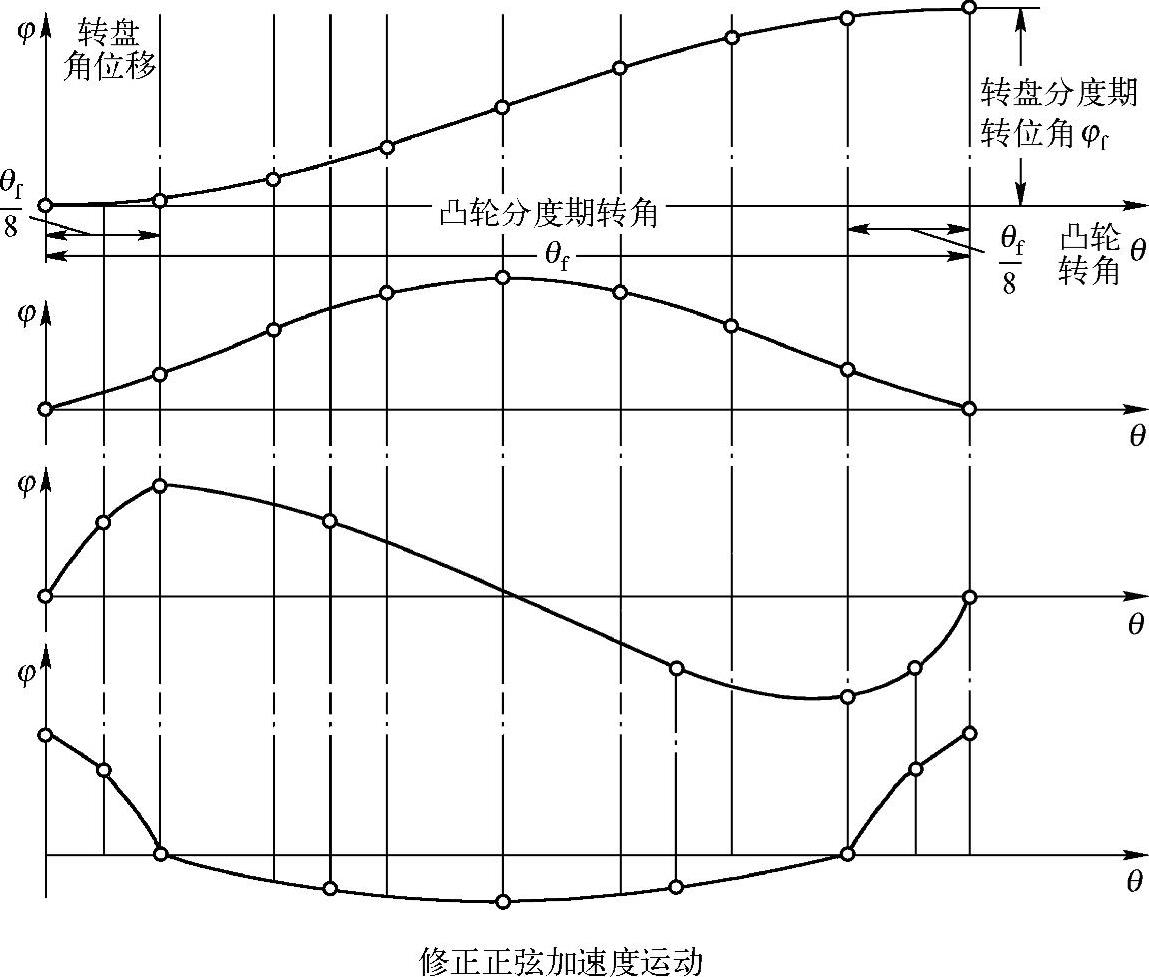
图11-9 组合摆线运动线图

组合摆线的运动规律特征是：

1）速度因数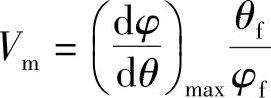。对于非平底形式的从动件，它影响机构的压力角。

2）加速度因数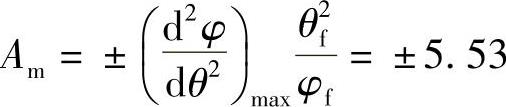。它影响凸轮机构的接触应力。(www.xing528.com)

3）跃动因数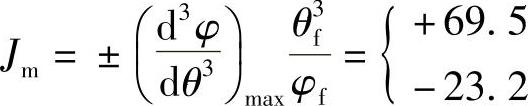。它表示从动件系统惯性系统的变化率。

4）惯性矩因数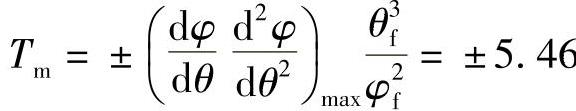。它是基于负荷惯性的关于凸轮轴转矩的变量，电动机的峰值动力与它有关。

上述各式中，φ（°）是转盘角位移，φ_f（°）是转盘分度期转位角；θ（°）是凸轮转角，θ_f（°）是凸轮分度期转角。

(8)转盘分度期的运动分析 在组合摆线运动三个区段的类角位移、类角速度、类角加速度和跃度为

1）当凸轮角位移0°≤θ≤22.5°时的开始区段

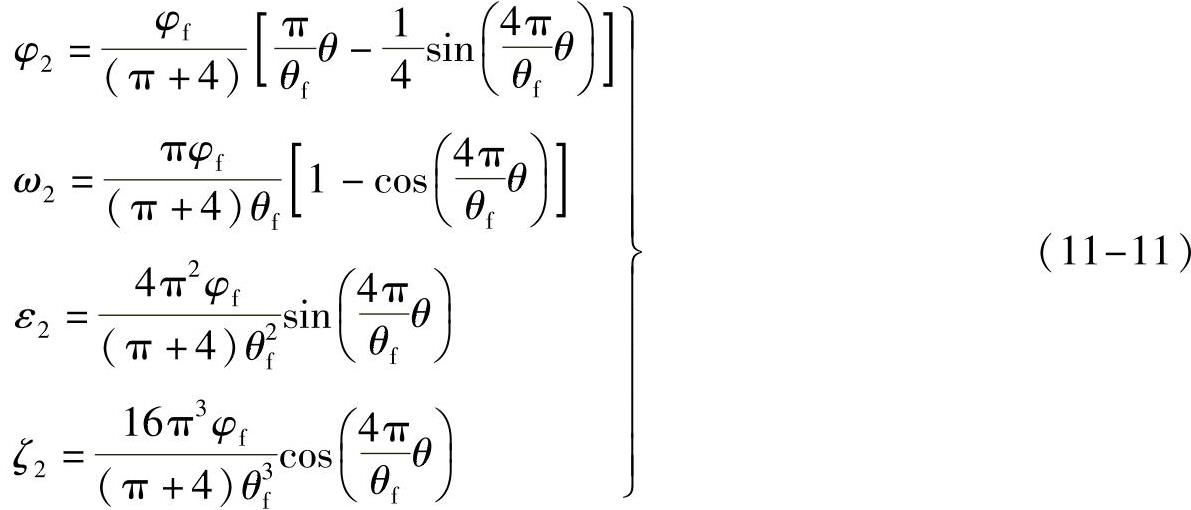
2）当凸轮角位移22.5°≤θ≤157.5°时的中间区段

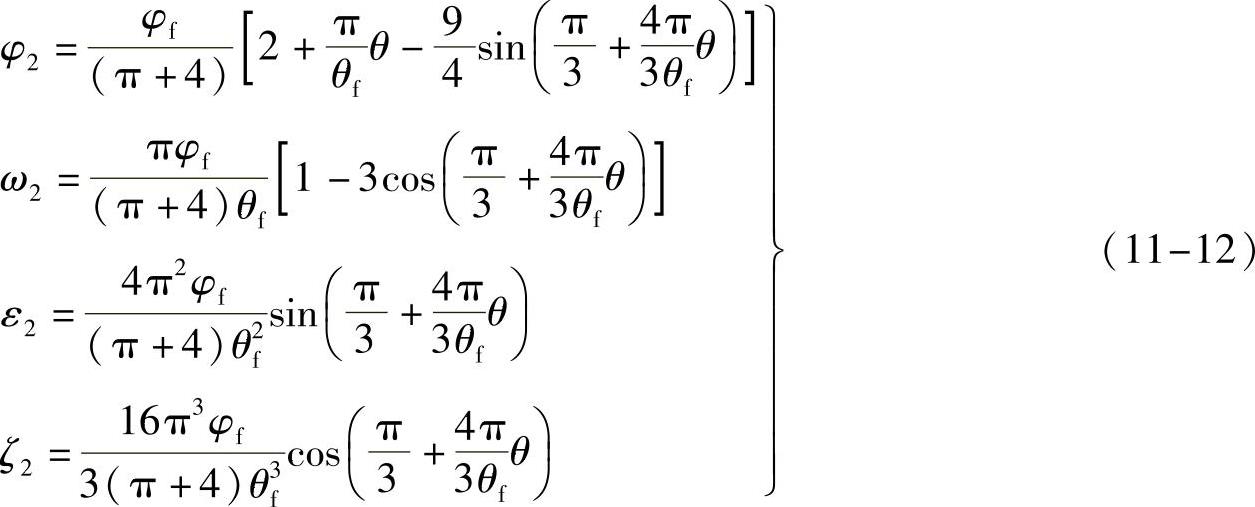
3）当凸轮角位移157.5°≤θ≤180°时的末尾区段

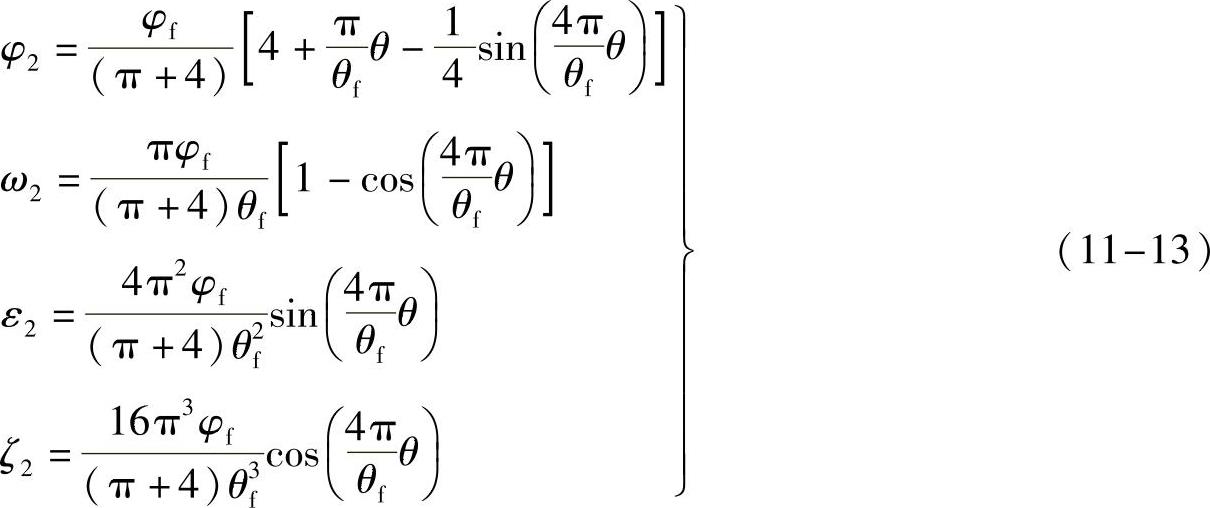
（9）机构在分度期的角速度比（ω₂/ω₁）和类角加速度（ε₂/ω²₁）根据式（11-11）～式（11-13）各式中间的两式，分别除以ω₁或ω²₁，得到角速度比（ω₂/ω₁）和类角加速度（ε₂/ω²₁）。

（10）机构动停比K和运动系数τ机构分度期时间t_f/s和停歇期时间t_d/s

机构动停比和运动系数