凸轮的设计和运动分析步骤及数学模型

1.凸轮设计和运动分析的步骤

1）输入已知的凸轮机构的结构参数，如凸轮基圆半径r_b、滚子半径r_t、偏置移动从动件的偏距e、从动件升程h、凸轮推程角φ、远休止角φ_s和回程运动角φ′等，以及运动和动力性能的许用值，如凸轮轮廓许用曲率半径[ρ]、推程许用压力角[α]和回程许用压力角[α′]等。

2）校核凸轮机构的推程和回程最大压力角α_max和α′_max，以及理论轮廓上最小曲率半径ρ_min，使其不超过规定的许用值[α]、[α′]和[ρ]，输出α_max、α′_max和ρ_min，及其在凸轮轮廓的位置角。

3）计算凸轮的理论轮廓坐标值（x，y）和实际轮廓坐标值（x′，y′）。

4）计算从动件的运动参数（位移s、速度v和加速度a），绘制从动件运动参数线图。

5）绘制凸轮轮廓图形。

2.建立凸轮设计的数学模型

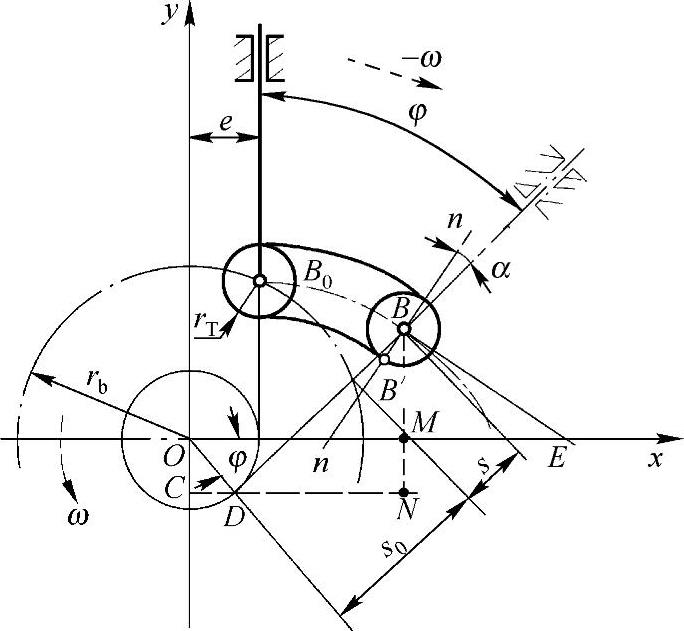
以典型的偏置移动从动件盘形凸轮机构设计为例（见图11-5）。

1）凸轮理论轮廓的直角坐标方程

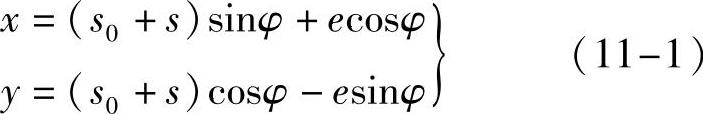
式中，φ是凸轮转角，s是从动件位移，s₀=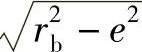是结构常数。

(www.xing528.com)

图11-5 偏置移动从动件盘形凸轮机构解析法分析

2）凸轮实际轮廓的直角坐标方程式

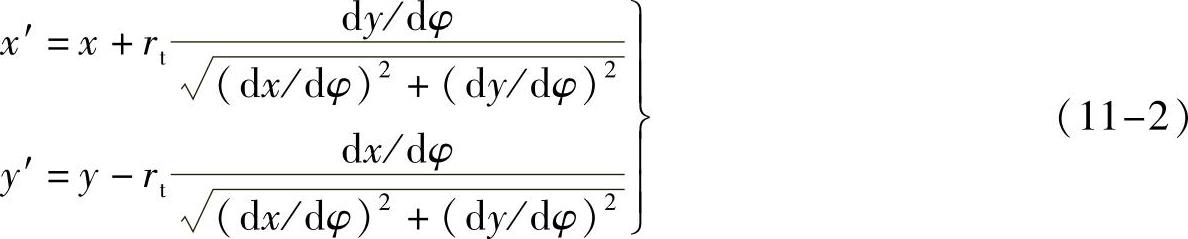
3）凸轮理论轮廓上的机构压力角

4）凸轮理论轮廓上的曲率半径

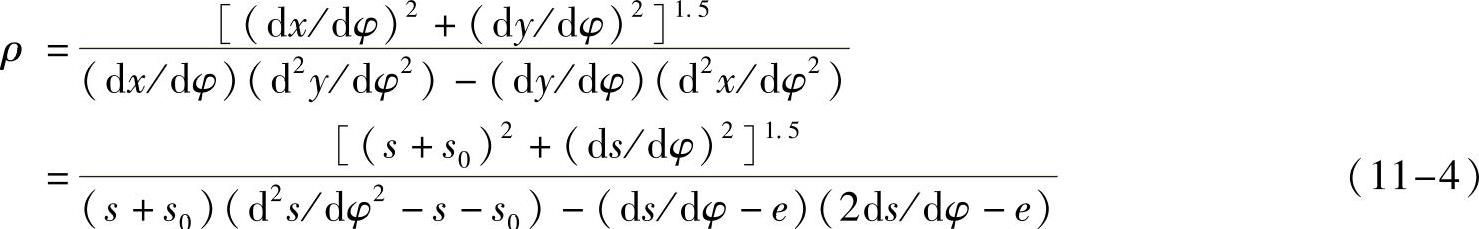
5）凸轮轮廓直角坐标的一阶和二阶导函数是

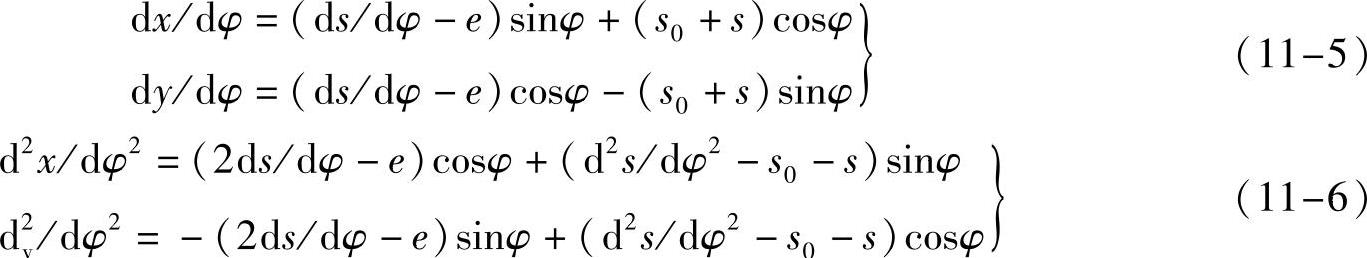
因此，采用解析法设计凸轮轮廓，需要根据给定的从动件运动规律s=f（φ），推导出对应的一阶导函数ds/dφ和二阶导函数d²s/dφ²（参考表11-2），然后代入到上述各式中进行计算。