1.搅拌杆空间对称旋轮轨迹的实现
在圆锥齿轮行星轮系中,圆锥行星轮7的轴线与中心圆锥齿轮6夹一个锐角(大小等于它们的轴交角),圆锥行星轮7公转时轴线在空间的轨迹是一个圆锥角为轴交角的正圆锥面。行星轮在自转时带动与其固定联接的搅拌杆一起绕其动轴线转动。因此,采用结构简单的圆锥齿轮行星轮系引导,可以使搅拌杆在容器中实现精确综合的空间对称运动轨迹。
与行星轮同步转动的搅拌杆臂上的某一动点A轨迹是旋轮线,从圆锥齿轮7与8的啮合展开平面(图10-11)可知其参数方程
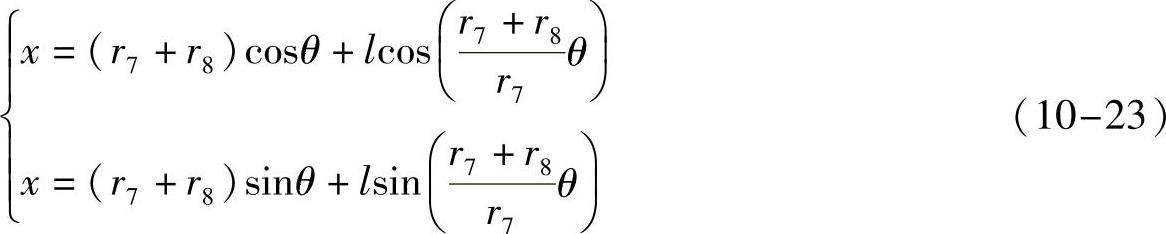
式中,r7和r8分别是行星轮7和中心内圆锥齿轮8的分度圆半径;l是动点A到行星轮轴心M的距离;θ是行星轮7绕中心内圆锥齿轮8公转的角位移。
采用MATLAB模拟二维旋轮线(见图10-13)和三维旋轮线(见图10-14)。由于该行星传动中行星轮7与中心内圆锥齿轮齿数比是z8/z7=36/11=3.27,因此在行星轮公转将近一周过程中,行星轮7自转带动固定连接的搅拌杆臂上的动点A形成三瓣旋轮线。
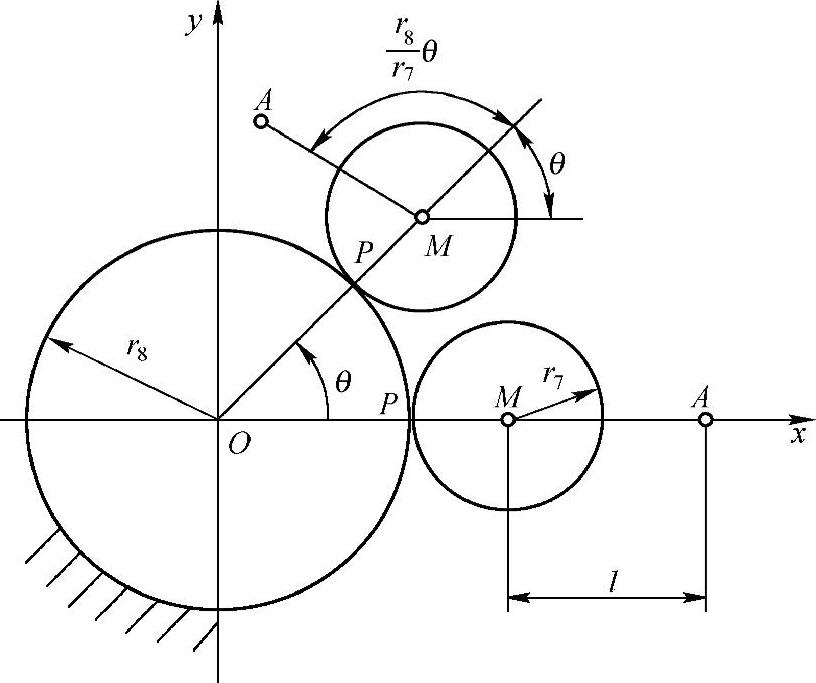
图10-11 行星传动运动分析
考虑到行星轮7与中心轮8的轴交角δ7+δ8=65.25°,因此搅拌杆臂上的动点实际形成空间旋轮线,实现容器内整体均匀的搅拌功能。
2.行星轮自转和公转运动分析
圆锥齿轮行星轮系运动简图如图10-12a所示。根据相对运动的合成原理,列出中心轮6、行星轮7与行星架H的角速度矢量关系式 (https://www.xing528.com)
(https://www.xing528.com)
因此 ω6+ω76=ωH+ω7H=ω7 (10-25)
式中,ω6是中心轮6的角速度;ωH是行星架H的角速度;ω76是行星轮7相对于中心轮6的角速度;ω7H是行星轮7相对于行星架H的角速度。
由矢量图解法得到如图10-12b所示的角速度矢量图。根据ω6、ω7和ω76组成角速度矢量三角形,得到行星轮绝对角速度

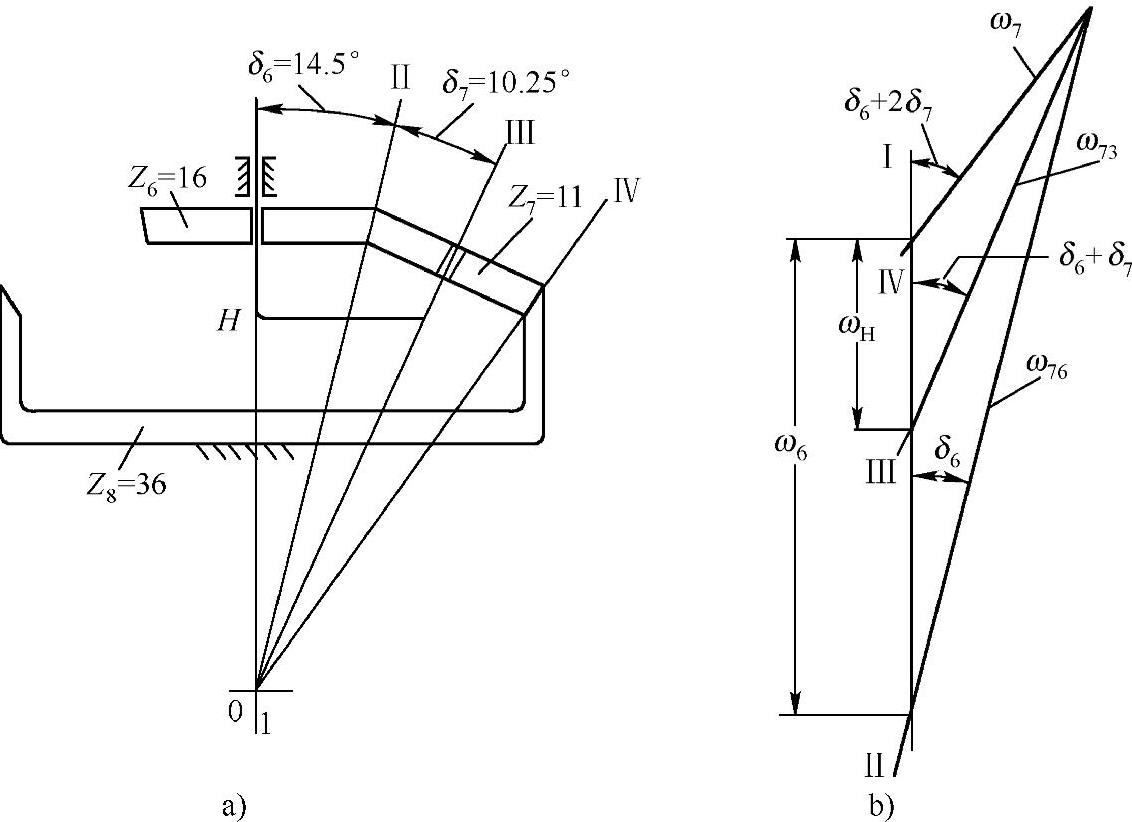
图10-12 圆锥齿轮行星传动的角速度矢量
根据ωH、ω7和ω7H组成角速度矢量三角形,得到行星架绝对角速度(即行星轮公转角速度)
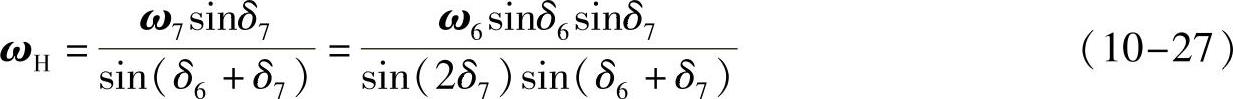
同理,行星轮7相对于行星架H角速度,即行星轮自转角速度
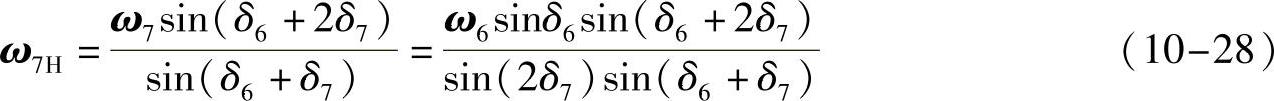
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




