针轮机构优化设计计算

例10-4 已知条件：星轮停歇数n=4，针轮动程角θ_d=π/2，星轮转位角φ_d=π/2，中心距C=192mm。

1）计算两轮的节圆半径比_μ。已知星轮上有n个锁止弧，则在针轮一个工作循环中星轮的停歇数为n，针轮与星轮的转角比σ=θ_d/φ_d，两轮的节圆半径比为μ。σ、μ、n三者关系是

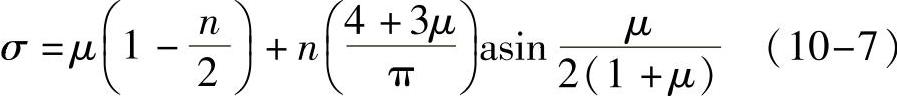
得到两轮的节圆半径比_μ。

在式（10-7）中代入转角比σ=θ_d/φ_d和停歇数n=4，采用MATLAB函数fzero求解超越方程（10-7），得到节圆半径比_μ=0.7773。

由于停歇数n是整数，转角比σ是整数或分数，节圆半径比_μ一般采用分数。因此利用MATLAB函数rat将计算得到的小数_μ转化为指定精度的分数_μ=7/9≈0.7778，可见与原值相差微小。

以下进行针轮机构的运动几何关系计算，相关参数如图10-7所示。

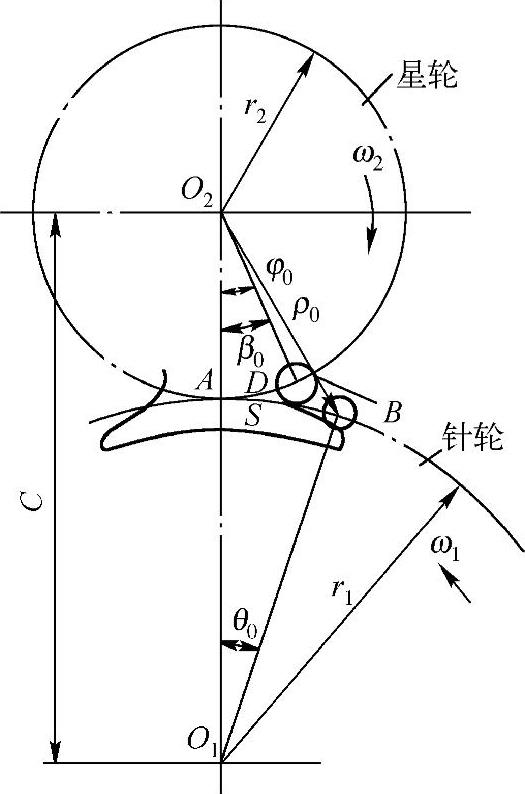
图10-7 外针轮机构的运动几何关系

2）计算星轮加速段对应的针轮转角θ0

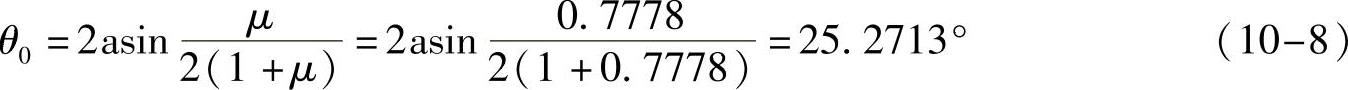
3）计算星轮齿槽外端中心位置角φ₀

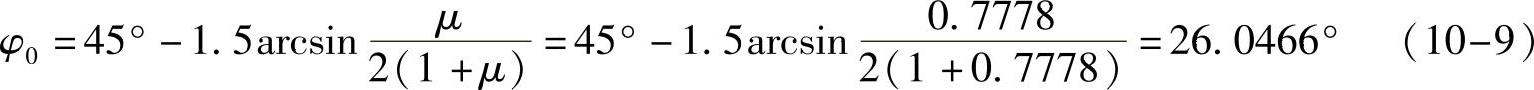
4）计算星轮齿槽内端中心位置角β0

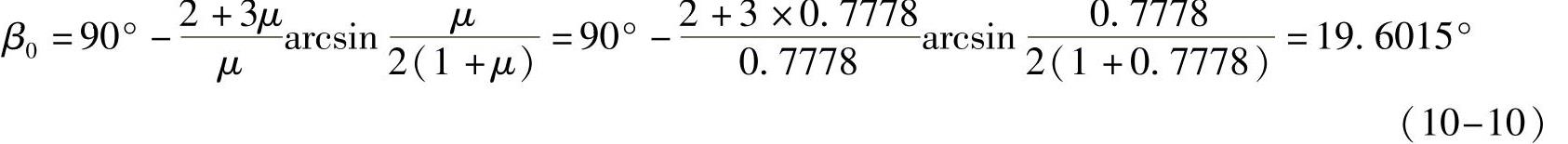
5）计算两轮节圆半径r₁与r2

6）计算星轮齿槽外端中心点B的半径ρ0

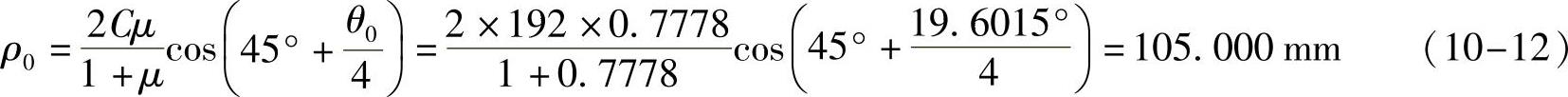(https://www.xing528.com)

7）计算针轮起始啮合位置弦长s

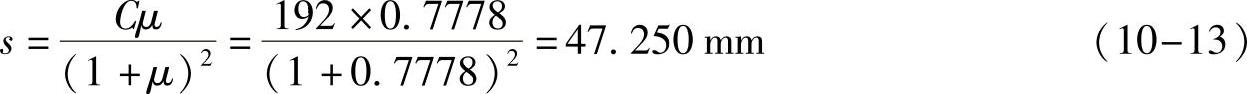
8）校核两轮转角比σ。计算两轮转角比的实际值

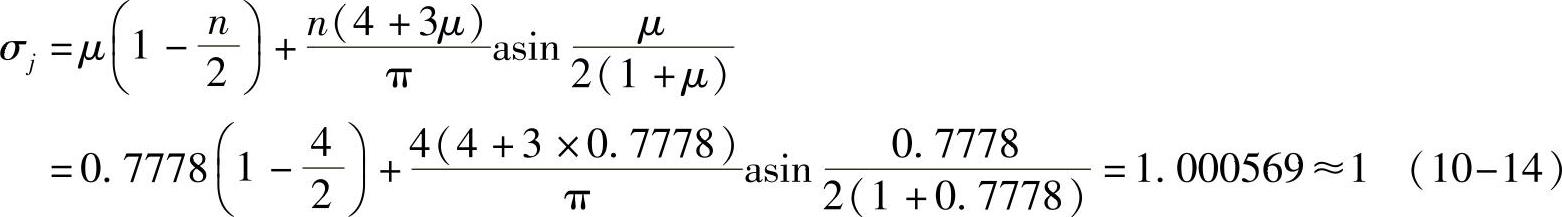
可见，两轮节圆半径比μ的微小变动对机构转角比的影响很小。

9）计算针轮锁止弧所对的中心角γ

10）计算星轮上齿槽中心线坐标（x，y）。星轮上齿槽中心线是外摆线，其直角坐标方程式为

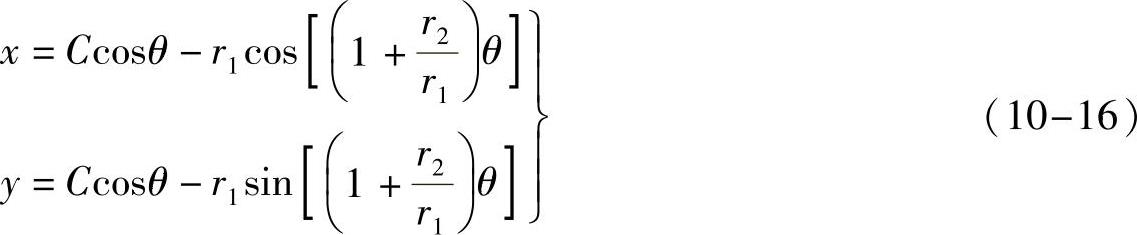
式中，θ是针轮转角。

11）计算星轮上齿槽廓线（包络线）坐标（x_k，y_k）

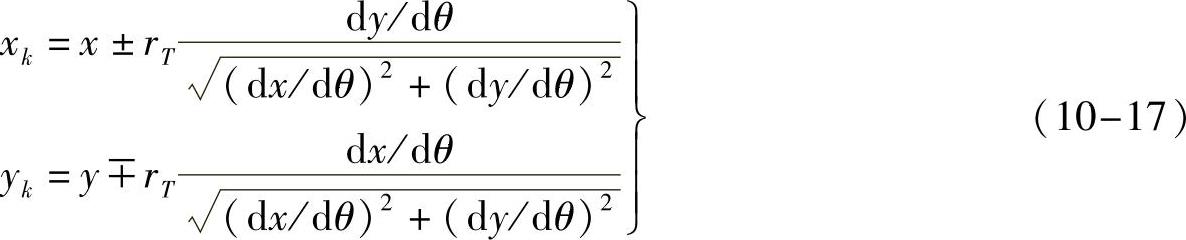
式中，上方的符号用于外包络线，下方的符号用于内包络线。

齿槽中心线坐标（x，y）对针轮转角θ的导数为

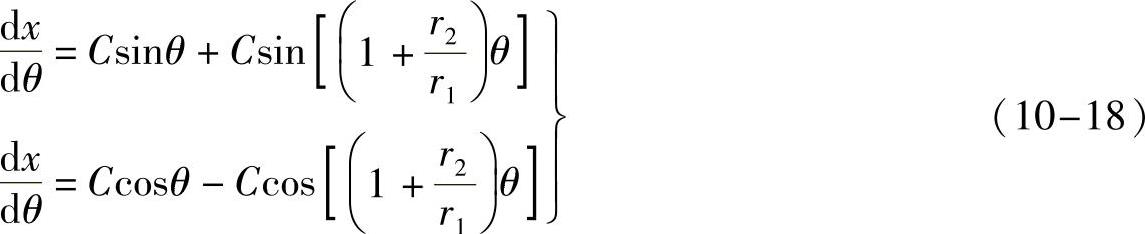
星轮齿槽中线和齿槽廓线如图10-8所示。

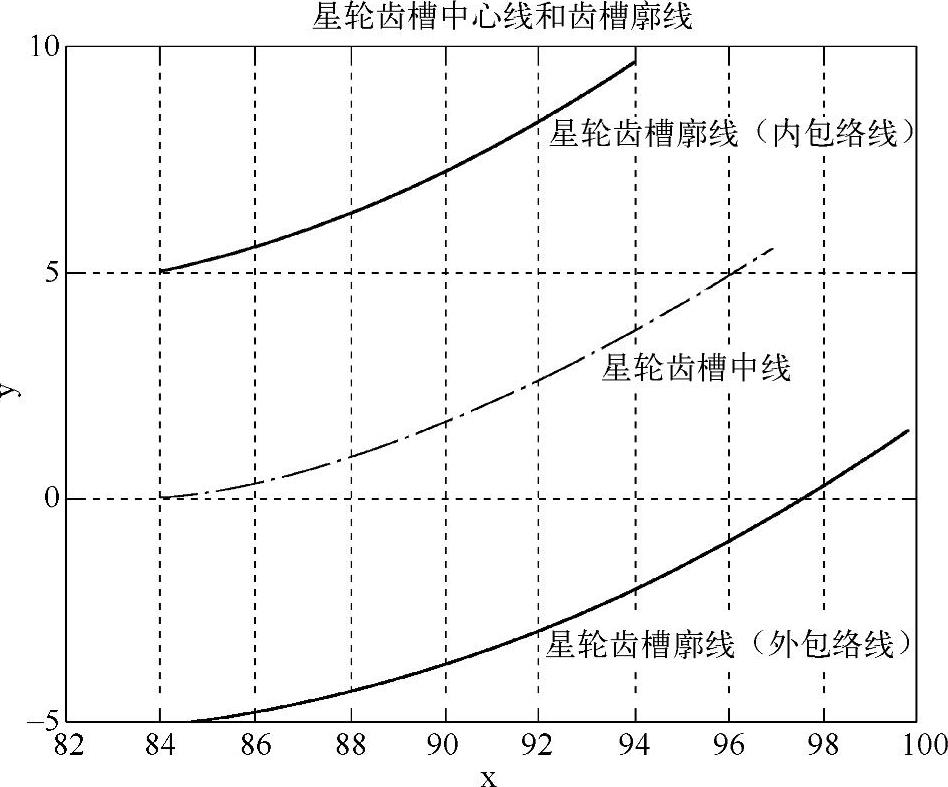
图10-8 星轮齿槽中线和齿槽廓线