如何编写M文件以计算实例并输出结果

例10-1 外槽轮机构的槽数z=4、6、8、10时，计算从动件槽轮的运动参数θ₃、ω₃、ε₃，并且绘制槽轮的运动线图（类角速度ω₃/ω₂和类角加速度ε₃/ω²₂）。

编制外槽轮机构运动分析的M文件：

M文件运行结果：

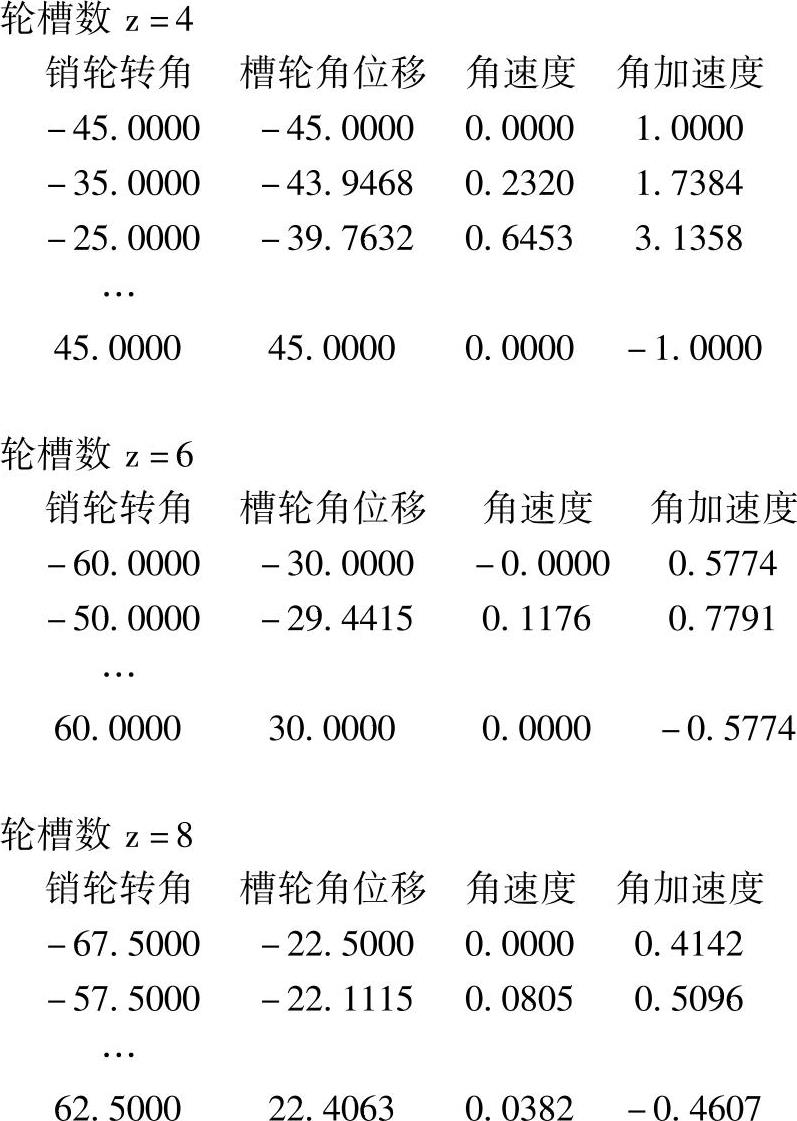
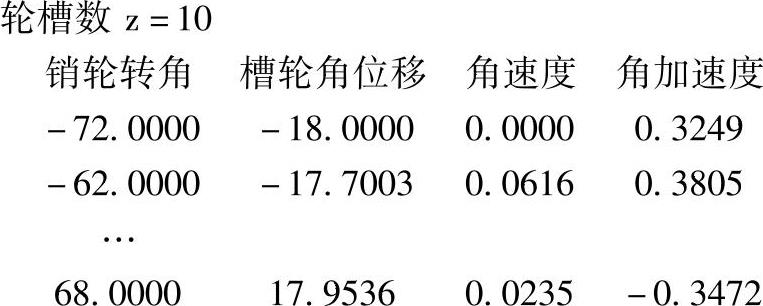
绘制的外槽轮机构运动线图如图10-2和10-3所示。

图10-3 外槽轮机构的类角速度和类角加速度运动线图

从图10-3可以看出，随着槽轮槽数z的增大，外槽轮机构的运动趋于平稳，动力特性也得到改善。但是槽数过多会使槽轮的体积过大，产生较大的惯性力矩。因此，槽轮的槽数一般取z=4～8。

例10-2 内槽轮机构的槽数z=4、6、8、10时，计算从动件槽轮的运动参数θ₃、ω₃、ε₃，并且绘制槽轮的运动线图（类角速度ω₃/ω₂和类角加速度ε₃/ω²₂）。

编制内槽轮机构运动分析的M文件：

运算结果：

绘制的内槽轮机构运动线图如图10-4和图10-5所示。

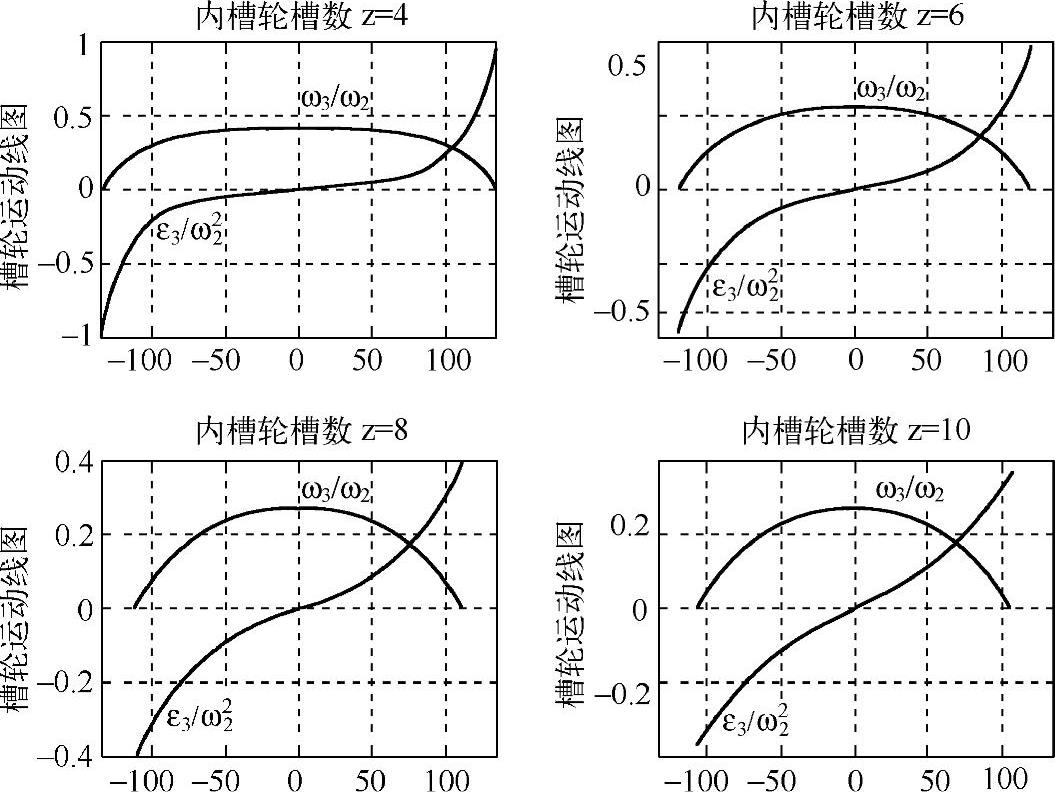
图10-4 不同槽数时内槽轮机构的运动线图

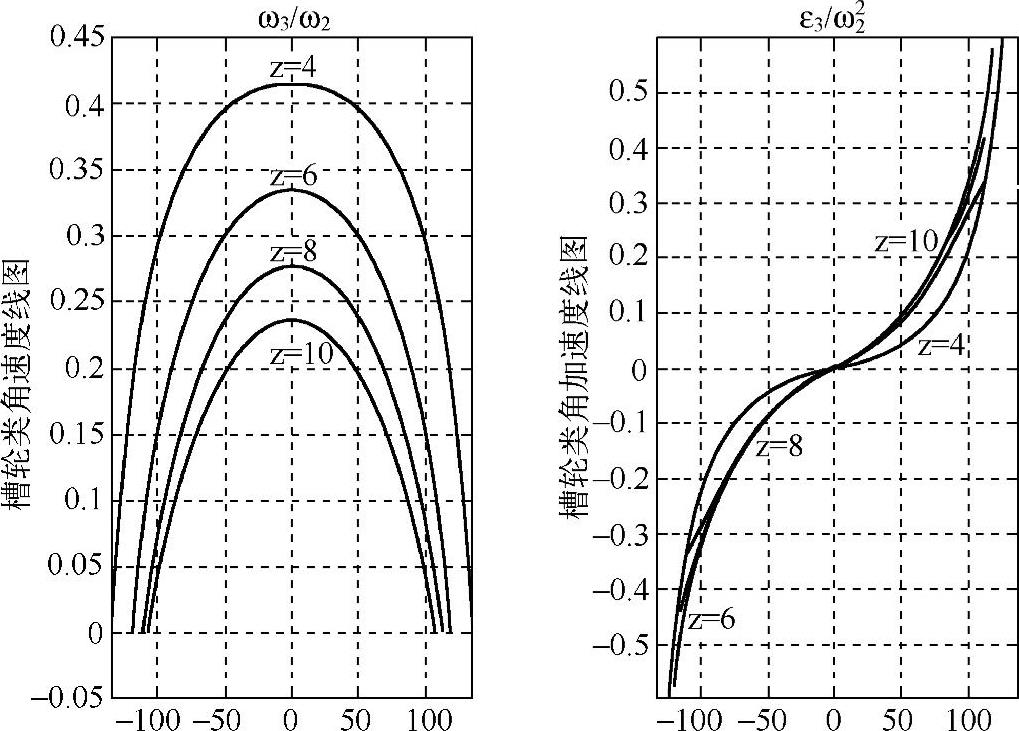
图10-5 内槽轮机构的类角速度和类角加速度运动线图

从图10-5可以看出，随着槽轮槽数z的增大，内槽轮机构的类角速度降低，但是它们的类角加速度与槽轮槽数z的关系不十分明显。

例10-3 某12工位转盘设备采用单圆销外槽轮机构实现转位，最长工序的工艺时间1.4s，槽轮机构中心距a=120mm，槽轮轴上等效转动惯量J_3v=150kg·m²。试计算机构运动系数τ、拨盘的转速n₂、槽轮机构的结构尺寸和所需要的电动机功率。

说明：MATLAB默认的运算精度是双精度的，但是一般书上显示计算结果只保留4位小数，所以表面上M文件计算结果与依照公式手算结果在最后一两位小数可能有差异，实际上是不可能的。下面的所有计算实例都如此。

解：

1）计算机构运动系数τ：槽轮的槽数等于转盘设备的工位数，即z=12。由于圆销数k=1，根据参考文献[1]式（6-7）得到外槽轮机构的运动系数

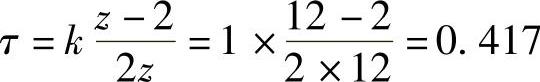
2）确定拨盘的转速n₁和设备的生产率Q：在槽轮静止时，设备处于工艺动作状态，因此最长工序的工艺时间就是槽轮的静止时间t′₂，根据参考文献[1]式（6-6）得到机构的运动循环周期

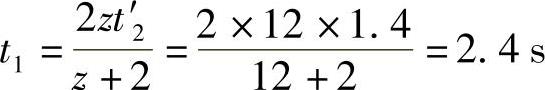
拨盘的转速为

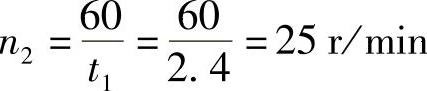(https://www.xing528.com)

设备的生产率为

Q=60n₂=60×25=1500/h

3）计算槽轮机构的几何尺寸（参考文献[1]表6-3）：拨杆2上圆销转动半径为

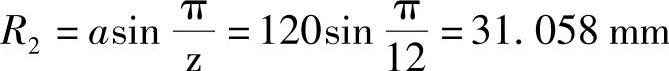
取R₂=31mm。

槽轮半径为

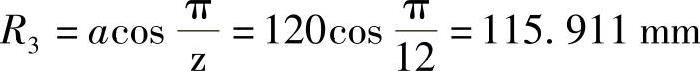
取R₃=116mm。

根据结构取圆销半径r=8mm，槽顶口壁厚e=5mm，则槽底高

b≤a-（R₁+r）=120-（31+8）=81mm取b=76mm。

槽深为

h=R₃-b=116-76=40mm

锁住弧半径

R_x=R₂-r-e=31-8-5=18mm

锁住弧张开角

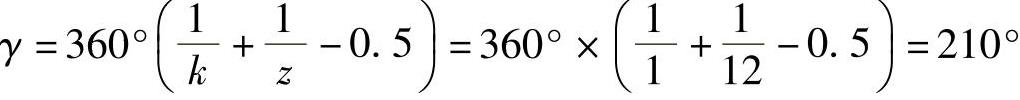
槽轮厚度根据结构取20mm。

4）计算槽轮3发生最大角加速度时拨杆2相应的位置角。圆销中心轨迹半径R₂与中心距a的比

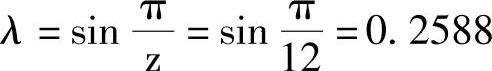
槽轮最大加速度时拨销的位置角

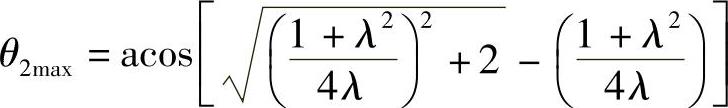
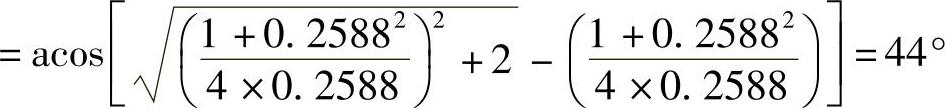
拨盘轴上的最大转矩

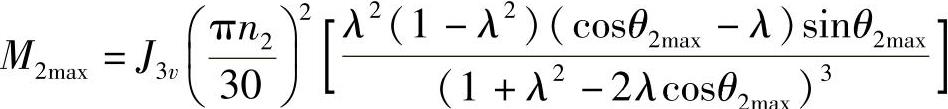
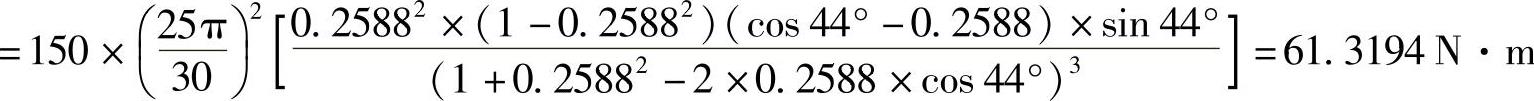
拨盘轴上的输入功率

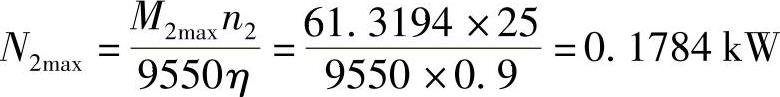
5）绘制槽轮和拨盘的工作图，如参考文献[1]图6-20所示。

编制M文件如下：

计算结果：