优化设计：实现预定函数的最佳方案

用从动件与原动件的转角关系ψ_s=f（φ）来模拟已知函数ψ=f（φ），是一种实现函数的机构综合问题。机构综合理论证明，曲柄摇杆机构采用常规的几何综合法或解析综合法，至多能够精确再现连架杆的五组对应位置。如果要求机构在更多的位置上最佳地逼近预期函数值，而且对机构的参数值有一定的限制，必须采用优化综合法。

例9-3 要求设计一个曲柄摇杆机构，当原动件曲柄的转角时，要求从动件摇杆的输出角实现函数。其中，φ₀，ψ₀分别为对应摇杆在右极限位置时，曲柄和摇杆的初始位置角，以水平机架方向逆时针计量。要求机构传动角范围是45°≤γ≤135°，取曲柄长度为单位长度l₁=1，根据机器结构取机架相对长度l₄=5。

1.建立优化设计的数学模型

（1）确定设计变量 曲柄摇杆机构按照原动件和从动件角度对应关系，独立参数有三杆相对长度l₂、l₃、l₄及曲柄和摇杆的初始位置角φ₀，ψ₀5个。如图9-3所示，如果取机构的右极限位置时两连架杆与机架所夹的锐角作为初始位置角φ₀和ψ₀，则它们可以根据该位置的几何关系确定

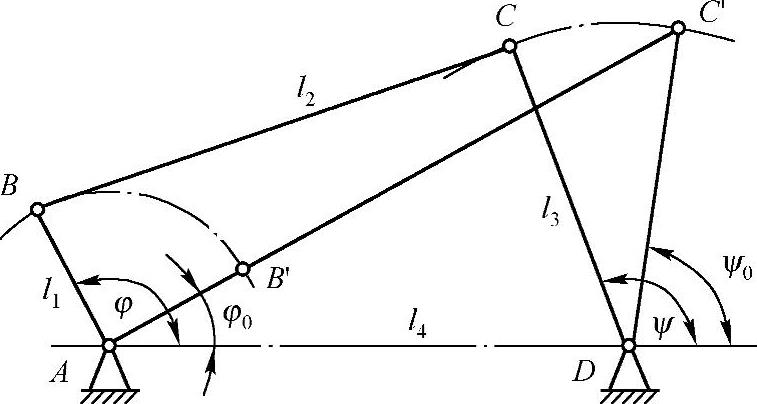
图9-3 曲柄摇杆机构的初始位置角

并且不再是独立参数。

根据题意曲柄长度为单位长度l₁=1和机架长度l₄=5已经给定。因此，选择机构的连杆长度l₂和摇杆长度l₃作为设计变量

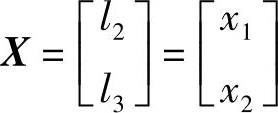
这是一个二维优化设计问题。

（2）建立目标函数 取机构输出角的平方偏差最小为设计目标

式中，ψ_i是期望输出角，根据题意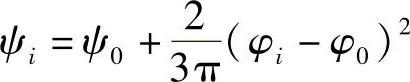，其中

式中，设曲柄转角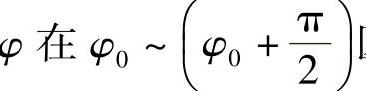区间内均匀的离散点数为s；i是各个离散点的序号。ψ_si是实际输出角，根据机构的运动几何关系确定（图9-4）

图9-4 曲柄摇杆机构的输出角

其中，根据△BDC和△ABD及余弦定理，得到

（3）确定约束条件(www.xing528.com)

①为了使机构的传力性能良好，机构的最小传动角γ_min≥45°或最大传动角γ_max≥135°。曲柄在与机架共线的位置时，机构有最小或最大传动角，如图9-5所示。根据机构在该两个位置的余弦定理

经过整理，得到约束方程

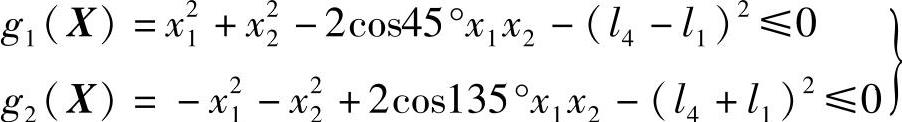
②根据曲柄存在的杆长之和条件（曲柄摇杆机构中，曲柄是最短杆，最短杆与最长杆的长度之和不大于其余两杆长度之和），经过整理得到约束条件

2.二维优化设计平面分析

绘制出该优化设计问题的设计平面，如图9-6所示。从图中可见，曲柄存在的杆长之和约束条件是不作用约束，起作用约束条件是机构传动角约束条件g₁（X）≤0和g₂（X）≤0，它们围成设计平面中的可行域。

图9-5 曲柄摇杆机构的最小和最大传动角位置

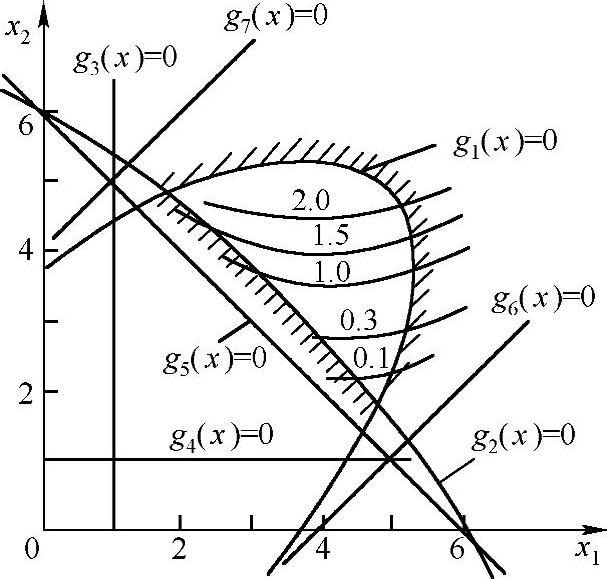
图9-6 曲柄摇杆机构的设计平面

综上所述，该优化问题的数学模型是

3.M文件和优化结果

在MATLAB平台上，根据优化设计数学模型建立目标函数和非线性不等式约束的两个函数文件；再建立设计变量的边界条件矩阵和非线性不等式系数矩阵，输入设计变量的初始值，使用MATLAB中计算多维约束优化函数fmincon运算，即可得到优化结果。

运算结果：

优化结果分析：连杆相对长度l₂=4.1236和摇杆相对长度l₃=2.3280，当曲柄在φ=φ₀～（φ₀+π/2）区间内转动时，摇杆输出角与期望实现函数ψ=f（φ）的平方偏差之和是f（X*）=0.0120，最优点位于约束边界g₂（X）=0上。