连架杆定位设计问题

1.建立机构的位置方程式

在如图9-2所示的铰链四杆机构中，已知机构主动件AB与从动件CD之间的位置对应

关系ψ=f（φ），根据各个构件长度在直角坐标系中的投影，建立机构的位置方程式

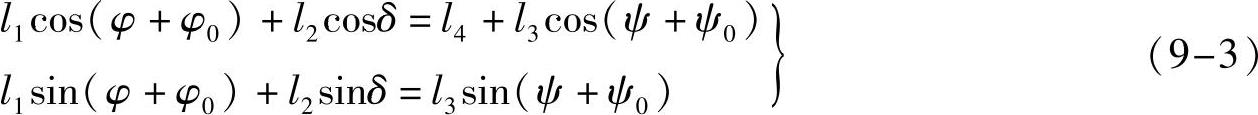
将上式整理后得到机构的位置方程式

l²₂=l²₁+l²₃+l²₄+2l₃l₄cos（ψ+ψ₀）-2l₁l₄cos（φ+φ₀）-2l₁l₃cos[（φ-ψ）+（φ₀-ψ₀）] （9-4）

因为连架杆的运动取决于各个构件的相对长度，设机构的相对杆件长度系数为

将它们代入机构的位置方程式（9-3），得到铰链四杆机构位置参数方程

R₁-R₂cos（φ_i+φ₀）+R₃cos（ψ_i+ψ₀）=cos[（φ_i-ψ_i）+（φ₀-ψ₀）] （9-6）

当已知两连架杆的对应位置关系ψ=f（φ）时，式（9-6）中有R₁、R₂、R₃、φ₀和ψ₀5个参数，说明在四杆机构常规设计中，能够满足两连架杆的对应位置数最多为5组。

2.计算实例和数学模型

例9-2 已知铰链四杆机构两连架杆AB和CD的初始位置角φ₀=ψ₀=0°，它们三组对应位置是φ₁=45°、ψ₁=52°；φ₂=90°、ψ₂=82°；φ₃=135°、ψ₃=112°，机架的长度l₄=50mm，要求设计该铰链四杆机构。

设计分析：将已知参数代入式（9-6），得到线性方程组(www.xing528.com)

R₁-R₂cos（φ_i+φ₀）+R₃cos（ψ_i+ψ₀）=cos[（φ_i-ψ_i）+（φ₀-ψ₀）]（i=1，2，3）

求解该线性方程组，得到机构的相对杆件长度系数R₁、R₂和R₃，再代入式（9-5），计算出三个未知构件的长度

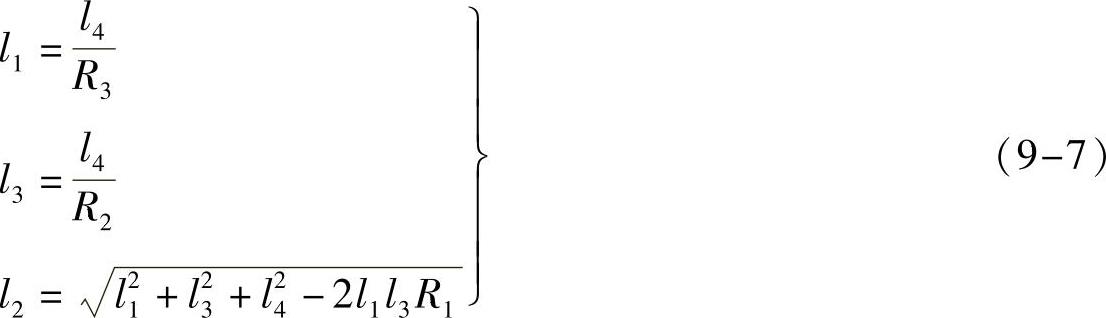
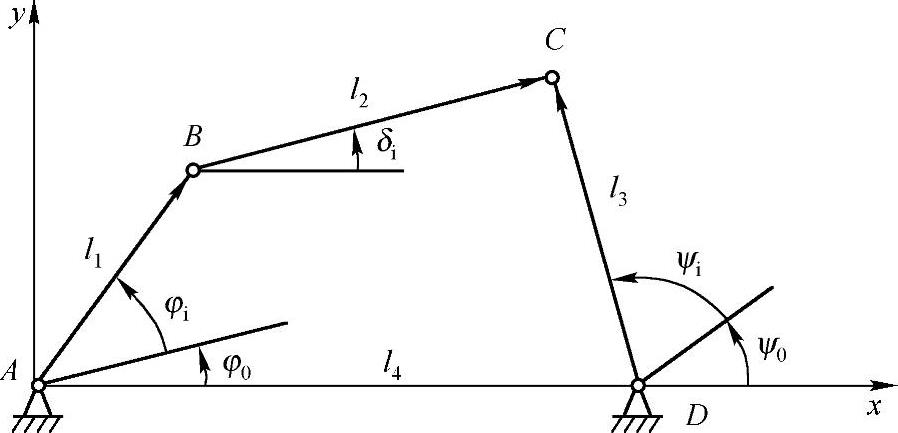
图9-2 铰链四杆机构连架杆的输入角和输出角

3.M文件和运算结果

在MATLAB平台上，首先输入已知数据：φ₀、ψ₀和[ψ_i，φ_i]（i=1，2，3），建立线性方程组的系数矩阵[a]和[b]；然后使用求逆函数inv或矩阵除法（运算符号“\”）求解线性方程组，直接求解出铰链四杆机构的杆长系数R₁、R₂和R₃；输入已知的机架长度l₄，按照式（9-7）计算出各杆长度。最后可以用求解矩阵或向量的范数的函数norm，检验计算结果的精度。

运算结果：

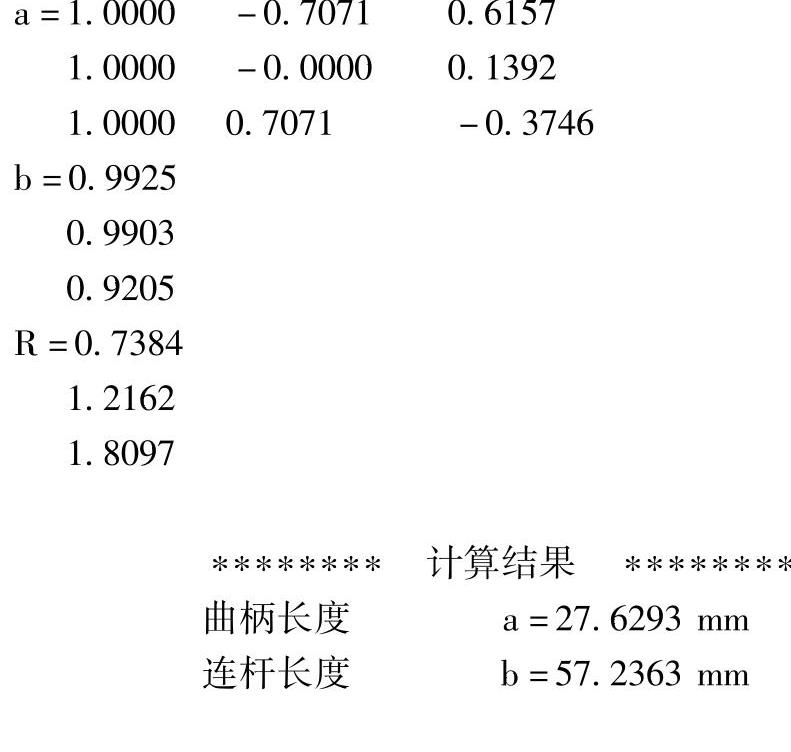
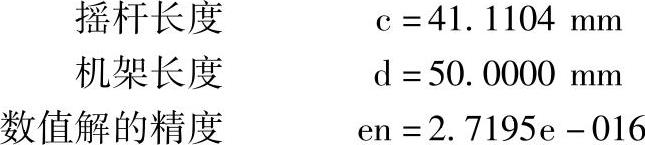
得到的计算结果是：曲柄长度l₁=a=27.6293mm，连杆长度l₂=b=57.2363mm，摇杆长度l₃=c=41.1104mm，机架长度l₄=d=50mm。

可见，采用求逆函数解线性方程组的误差是很小的，达到10^-16数量级。