设计问题：极限位置和最小传动角的给定

1.建立连杆机构的运动几何方程

铰链四杆机构如图9-1所示。设曲柄AB、连杆BC、摇杆CD和机架AD的长度分别为l₁、l₂、l₃、l₄，在机构两个极限位置和最小传动角位置组成的△AC₁C₂中，有如下几何关系

根据图9-1中所示四个三角形△AC₁C₂、△AC₁D、△AC₂D和△B′C′D及余弦定理得

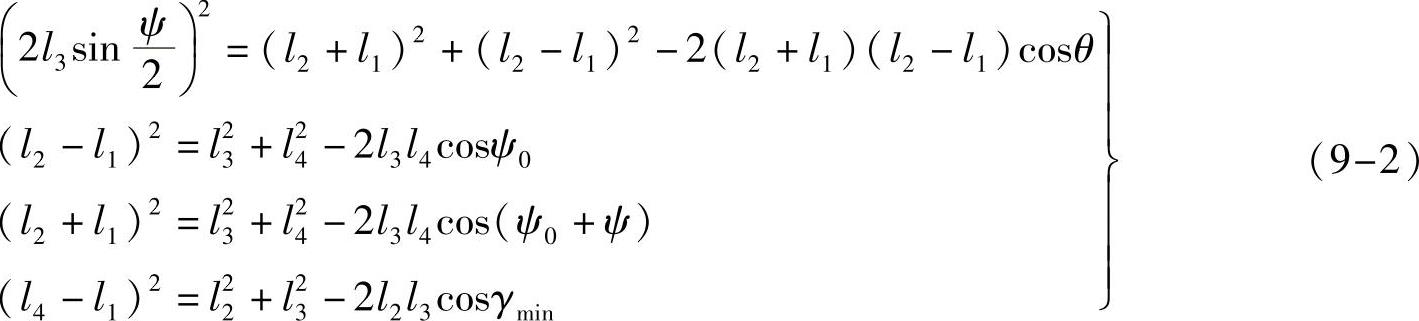
式（9-2表明了铰链四杆机构的运动几何关系，其中有8个参数。在已知四杆机构的极位夹角θ（或行程速度变化系数k）、摇杆长度L₃和摆角ψ的条件下，再补充最小传动角γ_min、曲柄长度l₁、连杆长度l₂、机架长度l₄等结构参数中的某个辅助条件，就可以通过求解非线性方程组（9-2）得到其他未知杆件长度，以及机构在左极限位置时摇杆位置角ψ₀。

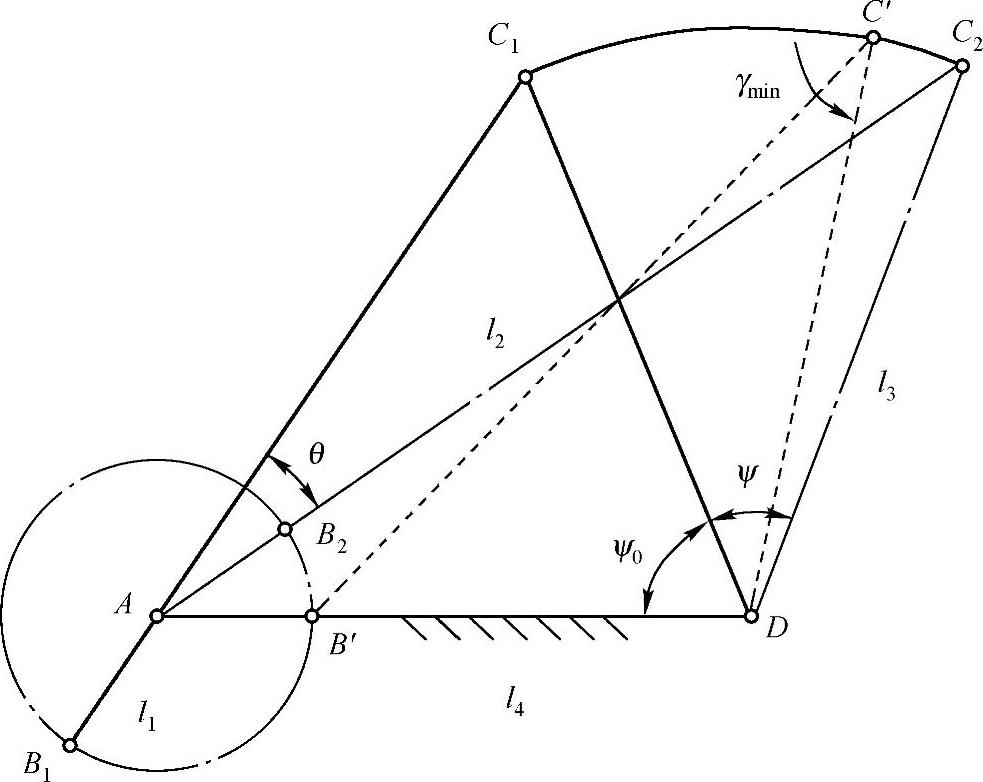
图9-1 铰链四杆机构的极限位置和最小传动角

2.计算实例和求解方法(www.xing528.com)

例9-1 试用解析综合法设计一个铰链四杆机构。已知机构行程速度变化系数k=1.25，摇杆CD的长度l₃=250mm，摆角ψ=30°，要求机构的最小传动角γ_min≥40°。

在MATLAB平台上，首先参照式（9-1）建立描述铰链四杆机构运动的运动几何方程的函数文件；输入极位夹角θ（根据行程速度变化系数k求出）、摇杆长度l₃、摆角ψ和最小传动角γ_min等已知数据，估计待求参数的初始值；然后使用非线性方程组的数值求解函数fsolve，可以方便地得到计算结果。

3.M文件和运算结果

运算结果：

得到的计算结果是：曲柄长度l₁=62.9934mm、连杆长度l₂=105.9045mm、机架长度l₄=245.0702mm，摇杆在左极限位置时的位置角ψ₀=9.8794°。