多目标规划问题简介

在规划问题中，目标函数是根据工程优化设计问题的主要准则厂(X)或几个设计准则f₁(X)、f₂(X)……来建立的。如果某项设计要求同时兼顾若干项设计目标达到最优，则属于多目标优化设计问题。其巾，由各项设计准则f₁(X)、f₂(X)……建立的目标函数，称为分目标函数。多目标优化问题要比单目标优化问题复杂得多。

对于单目标优化问题，任何两个解都可以用其目标函数值来比较方案的优劣。因此，最优解序列

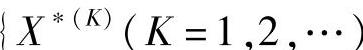
}是完全有序的。对于多目标优化问题，任何两个解不一定能够用其目标函数值比较方案的优劣，只能是半有序的。假设有两个设计方案X^(H)、X^(L)，如果它们各个分目标的函数值都满足条件

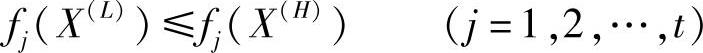
则方案

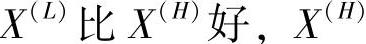
称为劣解。

能够获得使各分目标同时达到最优的绝对最优解是很困难的，目前在理论和算法上还没有完善的处理多目标优化方法。因为一个分目标的极小化往往会引起另外一些分目标的变化，它们的极小化甚至是矛盾和对立的。例如，工程优化设计中的技术性能要求往往与经济性指标的要求相互矛盾。因此，需要在各个分目标函数最优值之间进行协调，以便取得对各个分日标来说都算是比较好的方案。

由于多目标优化问题本身的复杂性，决定了求解多目标优化问题的困难性。处理单目标优化问题已经有许多有效的优化方法，可以将多目标优化问题转化为单目标优化问题，使多目标优化问题解的半有序性转化为单目标优化问题解的完全有序性。应当指出，这种转化后问题的解往往是原多目标优化问题的一个或部分非劣解，不是全部的非劣解。如何得到一个能够接受的最好非劣解，关键在于选择某种形式的折中。

MATLAB优化工具箱函数fgoalattain用于求解的多目标优化问题，也称为目标达到问题。其形式是：

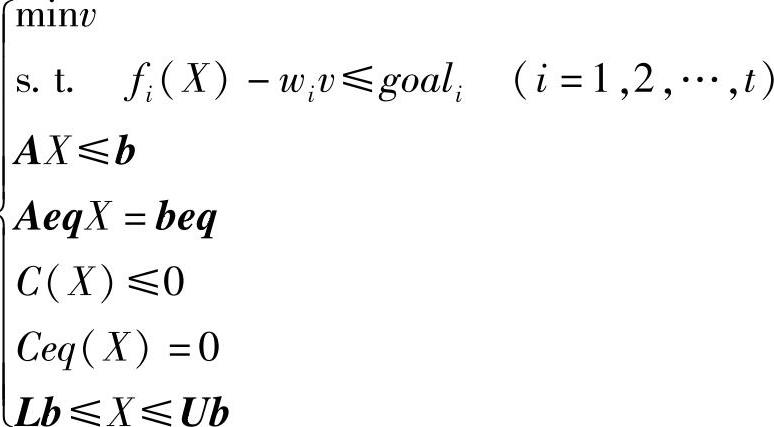
其中，ν是标量变量；f_i（X）（i=1，2，…，t）是各个分目标函数，goal_i和w_i是各个分目标及其权重向量。

函数fgoalattain的使用格式为：

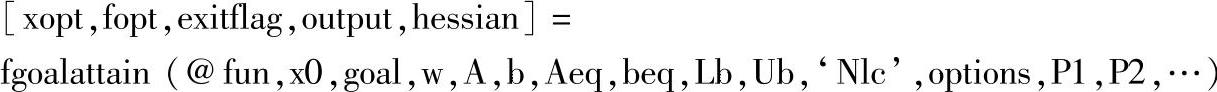
其中，输出参数有：

● xopt是返回目标函数的最优解。

● fopt是返回目标函数在最优解x点的函数值。

● exitflag是返回算法的终止标志。

● output是返回优化算法的信息的一个数据结构。

● hessian是返回目标函数在最优解x点的Hessian矩阵值。

输入参数有：(www.xing528.com)

● fun是调用目标函数的函数文件名。

● x0是初始点。

● goal各个分目标。

● w是各个分目标的权重。

● 线性不等式约束条件的系数矩阵A和常数向量b。

● 线性等式约束条件的系数矩阵Aeq和常数向量beq。

● 设计变量X的下界向量Lb和上界向量Ub。

● ‘Nlc’是定义非线性约束条件的函数名。

● options是设置优化选项参数，见表8-1。

● P1、P2等是传递给fun的附加参数。

例8-12 求解多目标线性规划问题：

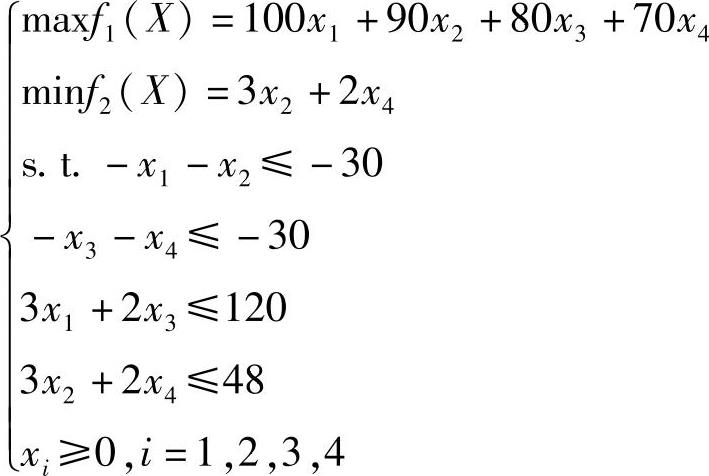
已知设计变量初值x0=[20，10，30，0]，分目标的初值f0=[10000，40]，分目标的权重w=[1，2e-4]。

编制目标函数文件：

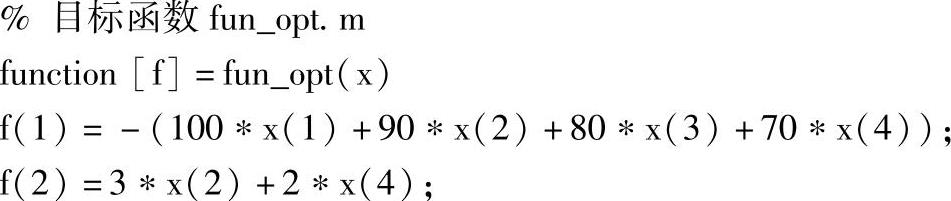
编制多目标优化函数调用文件：

计算结果：

说明：M文件运行输出的设计变量最优值X^*=[17.7035，12.2965，33.4447，0]^T和两个目标的最优函数值f（X^*）=[5552.6，36.9]^T。由于x₁*+x₂*=17.7035+12.2965=30，可见约束最优解X^*位于第一个线性不等式约束边界上。