如何解决二次规划问题

二次规划问题（Quadratic Programming）是最简单的非线性规划问题，其目标函数是二次函数，而约束函数是线性函数。由于二次规划问题的求解比较成熟，有时可以将一些求解比较困难的一般非线性约束规划问题转化为较易处理的序列二次规划子问题求解。

用于求解二次规划问题的MATLAB函数是quadprog，二次规划的数学模型表示为

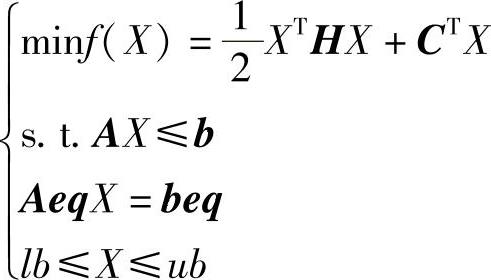
使用格式为：

[xopt，fopt]=quadprog（H，C，A，b，Aeq，beq，lb，ub，x0，options）

其中，输入参数有：

● H是目标函数的海色矩阵。

● C是目标函数设计变量一次项的系数向量。

● A和b分别是不等式约束函数的系数矩阵和常数向量。

● Aeq和beq分别是等式约束函数的系数矩阵和常数向量。

● lb和ub分别是设计变量的下限和上限。

● x0是初始点。

● options是设置优化选项参数，见表8-1。

输出参数有：xopt和fopt分别是返回目标函数的最优解及其函数值。(www.xing528.com)

例8-7 求解约束优化（二次规划）问题

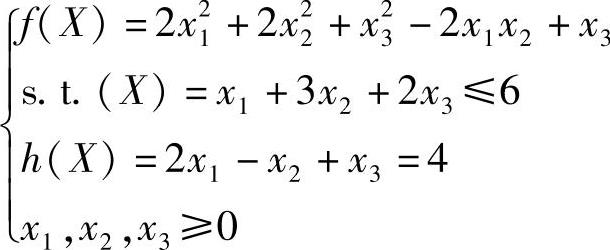
1）将目标函数写成二次函数的形式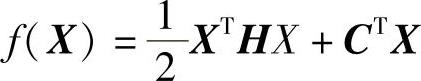，其中

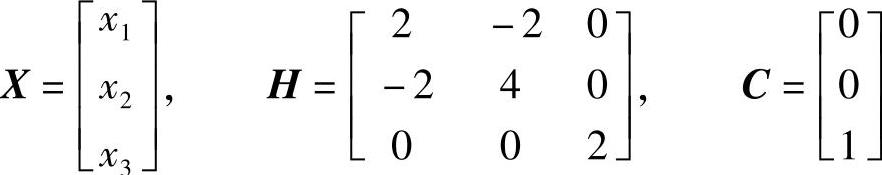
线性不等式约束函数的系数矩阵和常数向量为

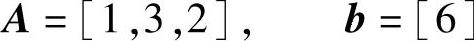
线性等式约束函数的系数矩阵和常数向量为

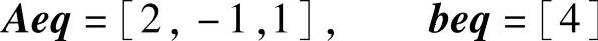
2）编制求解二次规划的M文件

M文件运行结果：

可见，二次规划的约束最优解X^*=[2.4783，1.0870，0.1304]^T位于不等式约束g（X）≤0和等式约束h（X）=0的交集。