解析线性规划问题

线性规划（Linear Programming）是数学规划中最简单和基本的问题，它主要用来解决在有限的资源条件下完成最多的任务，或是确定如何使用最少的资源统筹完成任务。

线性规划的数学模型包括决策变量X、约束条件和目标函数三个要素，它的决策变量是非负的，而且约束函数和目标函数都是线性函数。

线性规划的数学模型表示为：

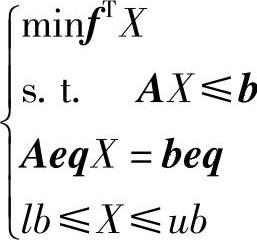
用于求解线性规划的MATLAB函数是linprog，其调用格式为：

[xopt，fopt]=linprog（f，A，b，Aeq，beq，lb，ub，x0，options）

其中，输入参数有：

● f是目标函数各维变量的系数向量。

● A和b分别是不等式约束函数的系数矩阵和常数向量。

● Aeq和beq分别是等式约束函数的系数矩阵和常数向量。

● lb和ub分别是设计变量的下限和上限。

● x0是初始点。

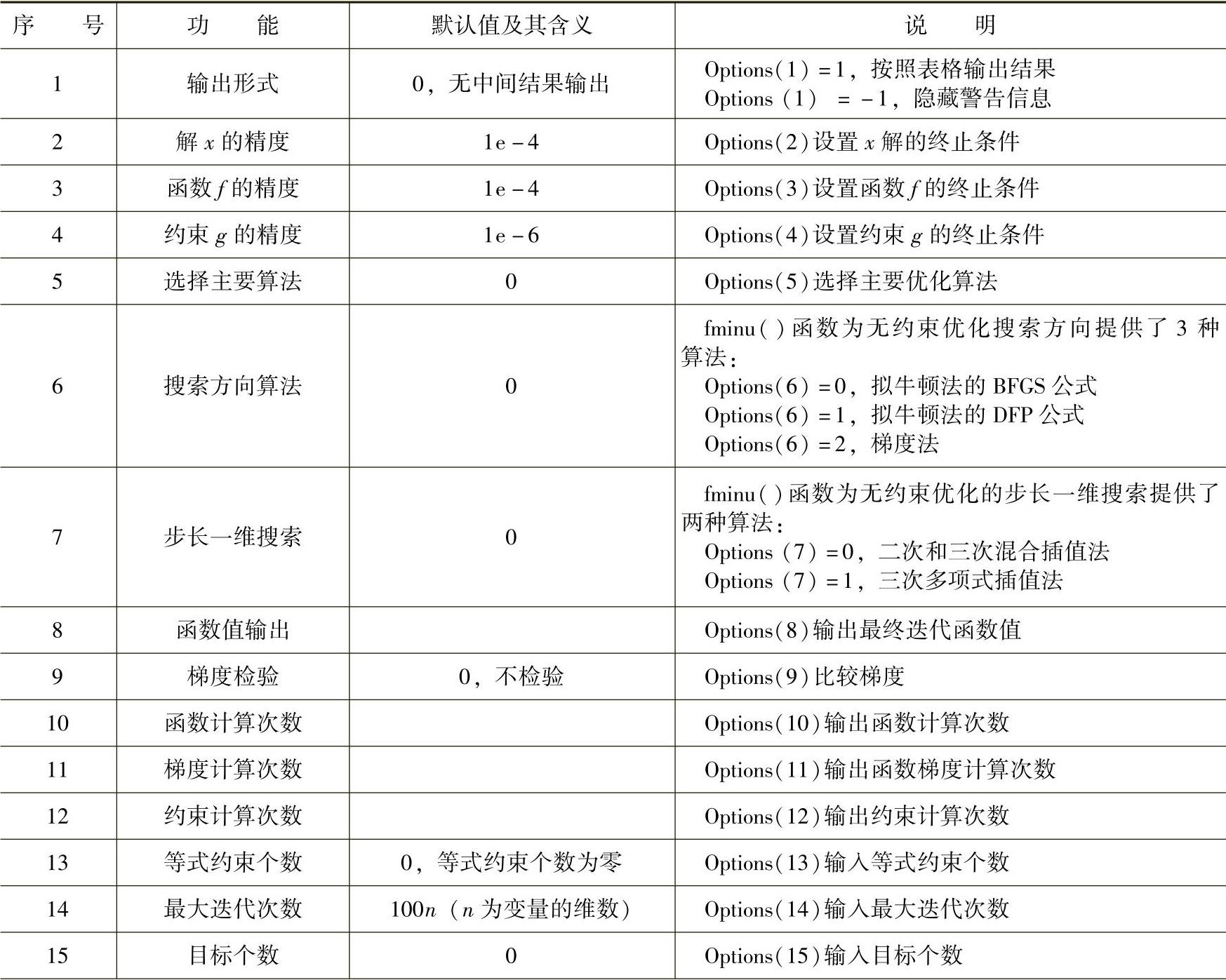
● options是设置优化选项参数，见表8-1。

输出参数有：xopt和fopt分别是返回目标函数的最优解及其函数值。(www.xing528.com)

例8-6 求解线性规划问题

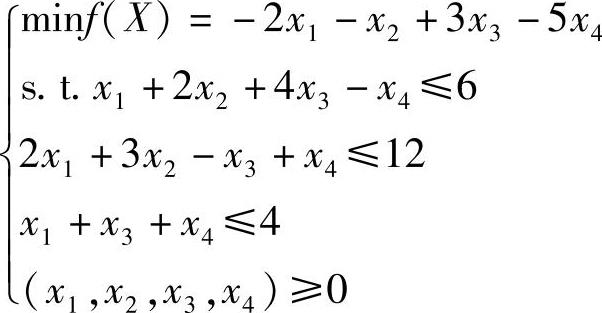
编制求解线性规划问题的M文件：

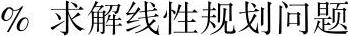
由于线性规划问题中没有等式约束，所以相应的系数矩阵Aeq和常数向量beq用空矩阵符号“[]”表示。程序运行结果：

可见，约束最优解位于两个边界约束x₁≥0和x₃≥0的交集上。

表8-1 控制参数Options

（续）