数值积分的梯形法和变步长辛普生法

求某函数的定积分时，在多数情况下，被积函数的原函数很难用初等函数表达出来；另外，许多实际问题中的被积函数往往是列表函数或其他形式的非连续函数。对这类函数只能使用数值积分计算函数的近似值。

1.梯形法求解数值积分

梯形法求解数值积分的基本思想是：将积分区间分割成许多足够小的分区间，取各个矩形的面积分别代替积分函数的曲线在各小段区间上围出来的曲边梯形的面积，再将所有这样的矩形面积加起来的总和，就近似地等于函数在这个区间上的定积分。

梯形法求解数值积分的函数调用格式是：

s=trapz（x，y）

其中，x是向量；y的行数应该等于x向量的元素数，如果y是多列矩阵，则可以得到若干个函数的积分值。

该函数适用于求解给定一组数据（x1，y1）、（x2，y2）、…的数值积分。

例7-10 用梯形法计算表7-2数据的定积分。

表7-2 列表数据

M文件运行结果：

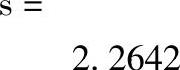
2.变步长辛普生法求解数值积分(www.xing528.com)

变步长辛普生法求解数值积分的基本思想是：在梯形法的基础上，将积分区间逐次分半，计算出每个子区间的定积分近似值，并且求和。

变步长辛普生法求解数值积分的函数调用格式是：

[s，n]=quadl（fun，a，b，tol）

其中，s是返回的定积分值；n是返回被积函数调用次数；fun是被积函数；a和b分别是定积分的下限和上限；tol是指定的积分精度（默认e=10^-6）。

该函数适用于求解给定函数的数值积分。

例7-11 用变步长辛普生法计算定积分。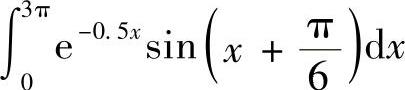

M文件运行结果如下，输出图形如图7-2所示。

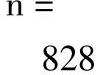
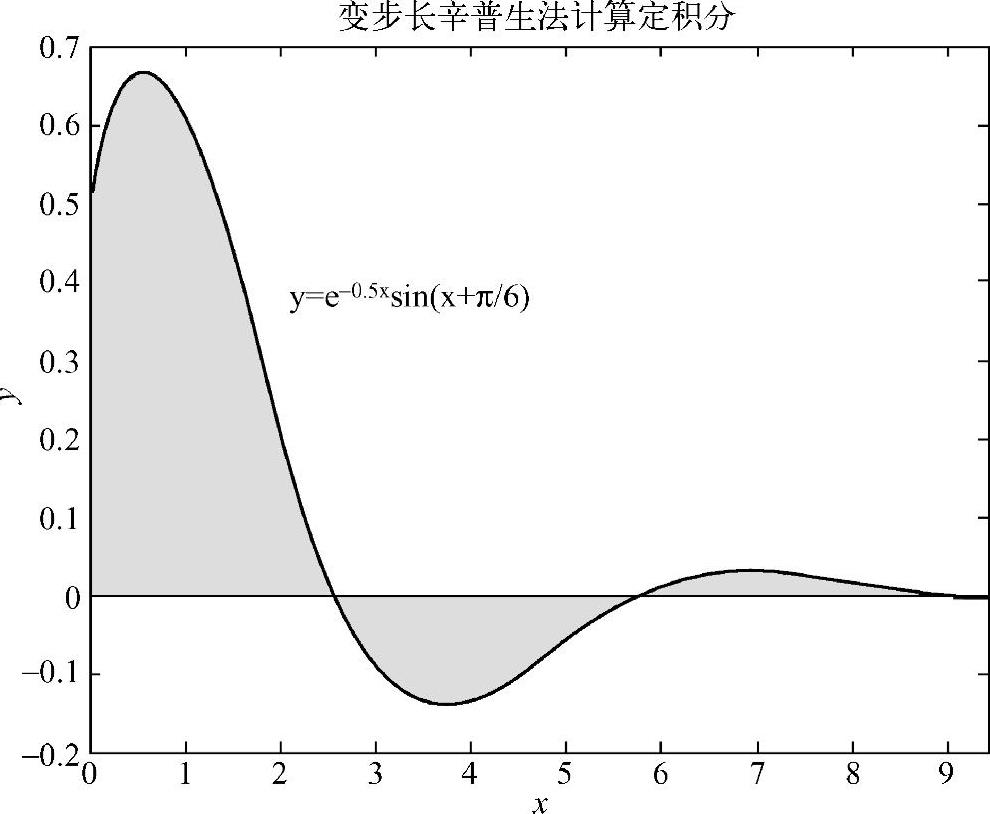
图7-2 变步长辛普生法计算定积分

M文件运算过程中总共调用函数828次。从图7-2可见，函数y=e^-0.5xsin（x+π/6）在区间（0，3π）上求积分，实际上就是求函数曲线y=f（x）与x轴、x=0和x=3π三条直线所围成的几个曲边形的面积。