实现二维数据插值的方法与技巧

1.二维网格数据插值

对于二维离散数据点（x，y）所在的平面矩形区域内，离散数据点（x，y）可以使用函数meshgid生成网格矩阵。进行二维网格数据插值的函数调用格式为：

y0=interp2（x，y，z，x0，y0，’k’）

其中，x和y是两个向量，分别描述两个参数的网格数据点；z是与网格数据点对应的函数值；x0和y0是需要插值的数据点，可以是标量或是向量；k是插值算法，与一维数据插值函数interp1的规定相同。

例6-7 给定二维函数z=（x²-2x）e^-x2-y2-xy离散得到的一些网格点，试使用3次样条插值方法，并且绘制网格点的三维图和插值拟合曲面图。

M文件运行结果如图6-3所示。其中，图6-3a所示是二维网格数据点三维图，图6-3b所示是选择较密集的插值点进行3次样条插值得到的曲面图。

2.二维分布数据插值

对于二维一般分布的离散数据点（x，y），进行二维数据插值的函数调用格式为：

y0=griddata(x，y，x0，y0，’v4’）

其中，x0和y0是需要插值的数据点，可以使用函数meshgid生成；v4是很圆滑的插值算法，效果很好。(www.xing528.com)

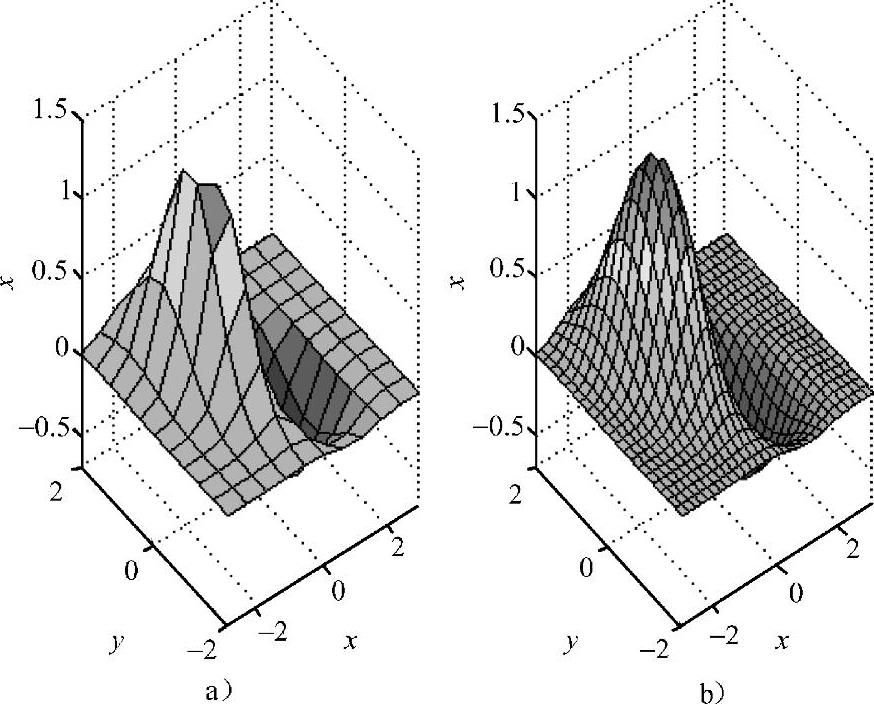
图6-3 二维网格数据的三维图和3次样条插值曲面图

例6-8 14个节点的二维离散数据点及其函数值见表6-2，试在x=70～200和y=0～150的区域内，按照间距为3生成插值点网格矩阵，使用3次多项式插值，并且绘制插值拟合曲面图。

表6-2 二维分布数据点及其函数值

编制M文件如下：

M文件运行结果如图6-4所示。其中，图6-4a所示是二维离散数据点的分布平面，图6-4b所示是选择较密集的插值点，进行3次多项式插值的曲面图。

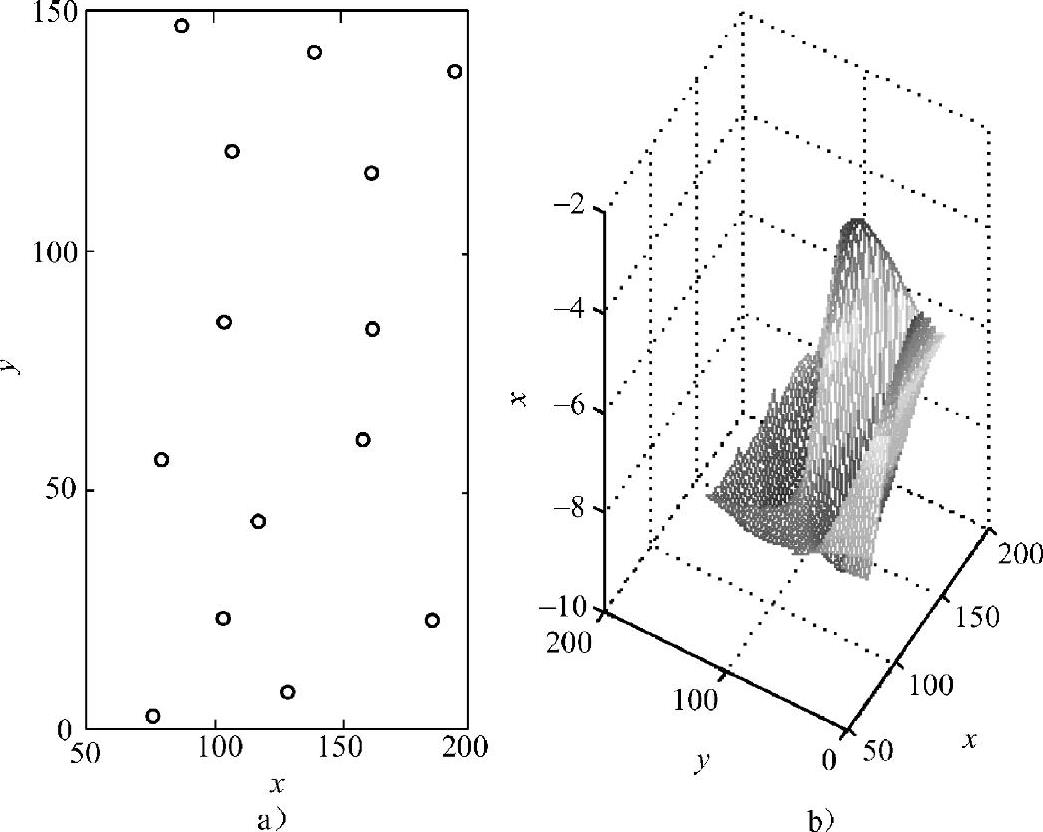
图6-4 二维离散数据的3次多项式插值拟合