一维数据的插值方法

1.一维数据插值函数

对于给定的n个插值节点x₁，x₂，…，x_n及对应的函数值y₁，y₂，…，y_n，一维数据插值函数调用格式是：

y0=interp1（x，y，x0，’k’）

它可以对插值区间内的任意插值点x₀的函数值y₀进行计算。其中，k是插值方法：

1）’linear’（默选值）是线性插值。它将与插值点x₀邻近的2个数据点用直线联接，然后在直线上选取插值点函数值y₀。

2）’nearest’是最近点等值插值。它根据插值点x₀与已知数据点远近程度，选取其中较近的数据点进行插值操作。

3）’cubic’是3次多项式插值。它根据插入已知数据点构造一个3次多项式y=g（x），然后计算插值点函数值y₀=g（x₀）。

4）’spline’是3次样条插值。它在每个分段内构造一个3次多项式，使其插值函数除了满足插值条件外，还要求在各个节点处满足光滑联接条件。

例6-5 已知实验数据来自一维函数y=x⁵e^-4x cosx在区间[0～4]内间距为0.2的离散值。试根据生成的数据进行插值处理，比较它们的插值结果。

M文件运行输出结果如图6-1和图6-2所示。

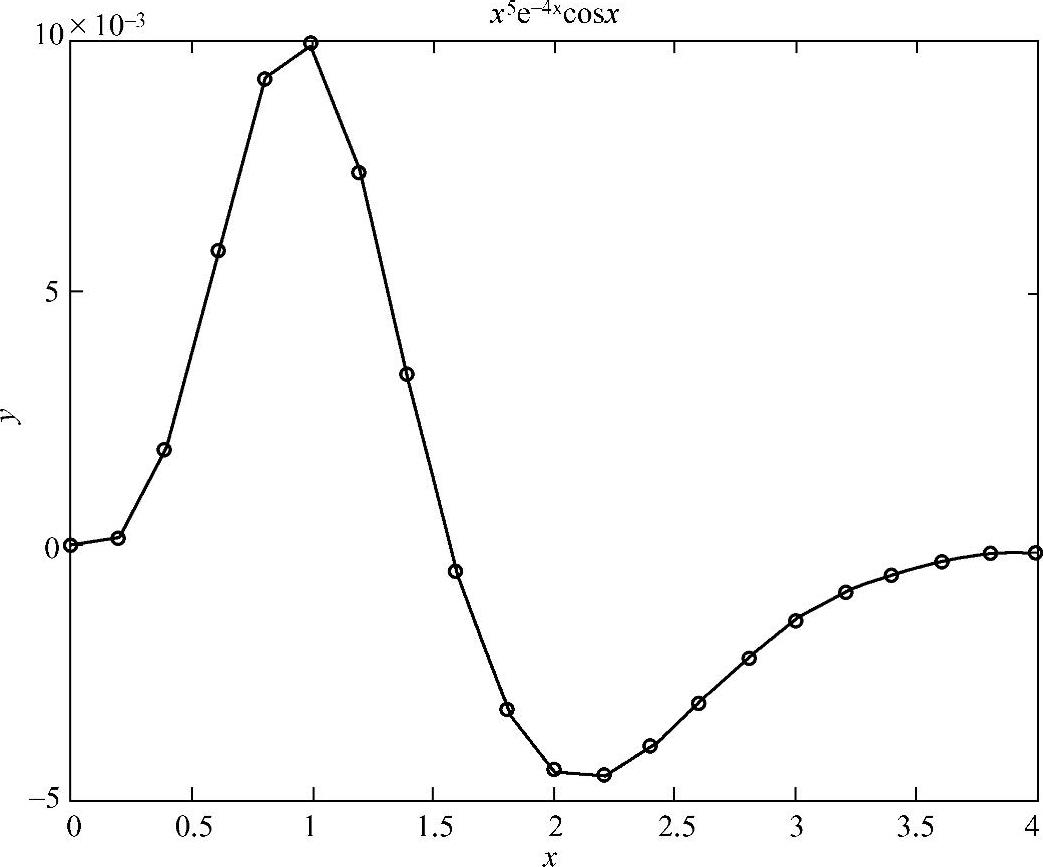
图6-1 一维离散数据线图

如图6-1所示，直接将离散数据点用直线联接起来形成的函数曲线比较粗糙，特别是在函数变化率较大的区间[0～2]内更为显著。

选择较密集的离散插值点，使用一维数据插值函数interp1（）进行插值拟合，如图6-2所示的各个子图，线性插值情况与图6-1所示的情况相同，最近点等值插值的拟合效果较差，3次多项式插值拟合效果较好，3次样条插值拟合效果最好。(www.xing528.com)

2.lagrange插值

对于给定的n个插值节点x₁，x₂，…，x_n及对应的函数值y₁，y₂，…，y_n，利用n次la-grannge插值多项式，对插值区间内的任意插值点x₀的函数值得计算公式为

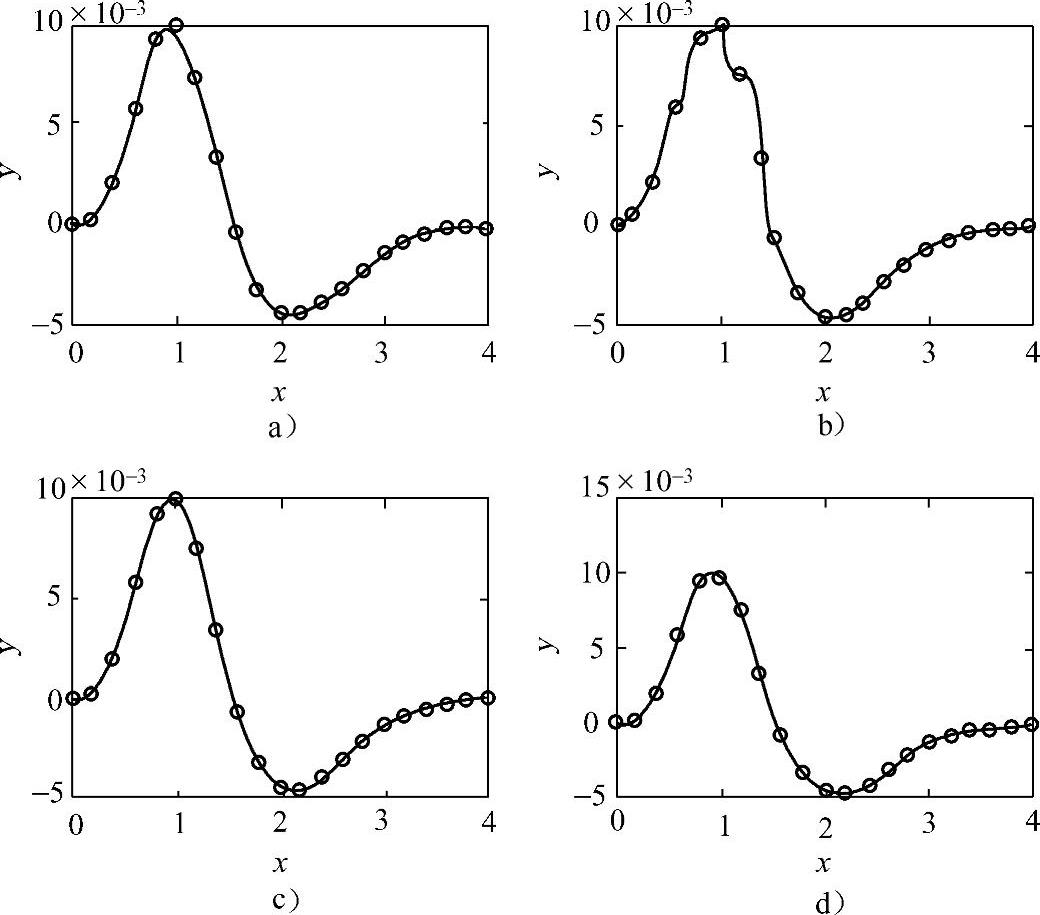
图6-2 一维离散数据插值拟合

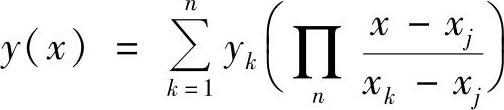
例6-6 自然对数函数y=ln（x）数表见表6-1，用lagrange插值计算ln（0.54）的值，并且检验计算精度。

表6-1 自然对数函数y=ln（x）数表

编制lagrange插值函数文件如下：

M文件运行结果：

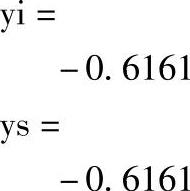
可见，采用lagrange插值可以获得足够的精度。