如何绘制三维曲面？

绘制三维曲面的主要内容包括：生成三维绘图数据[x，y]、由平面网格点矩阵[x，y]计算曲面函数矩阵z=f（x，y）和绘制三维曲面等步骤。

1.创建三维图形矩阵

1）生成平面网格点坐标矩阵：绘制二维函数z=f（x，y）的三维曲面图，首先在直角坐标系XOY平面上选定一个矩形区域D=[a，b]X[c，d]，将其分隔成m×n个小矩形的网格，m是X方向在[a，b]区域内的线性等分数，n是Y方向在[c，d]区域内的线性等分数，各个网格点的坐标的集合就是矩形区域D的平面网格坐标矩阵。

生成平面网格点坐标矩阵的函数调用格式是：

[X,Y]=meshgrid(X,Y)。

其中，输入参数（x，y）是两个行向量，x=a：d1：b，y=a：d2：b，d1与d2分别是X方向与Y方向网格的间距（d1=1或是d2=1可以省略）；输出参数[X，Y]中X是由行向量x的重复行组成的方阵，Y是由列向量y转置的重复列组成的方阵。

当输入参数x=y时，平面网格点坐标矩阵的函数调用格式为[X，Y]=meshgrid（x）。

例5-7 给定两个向量x=[1，2，3，4]和y=[2，3，4，5，6，7]，试生成平面网格点矩阵。

运算结果：

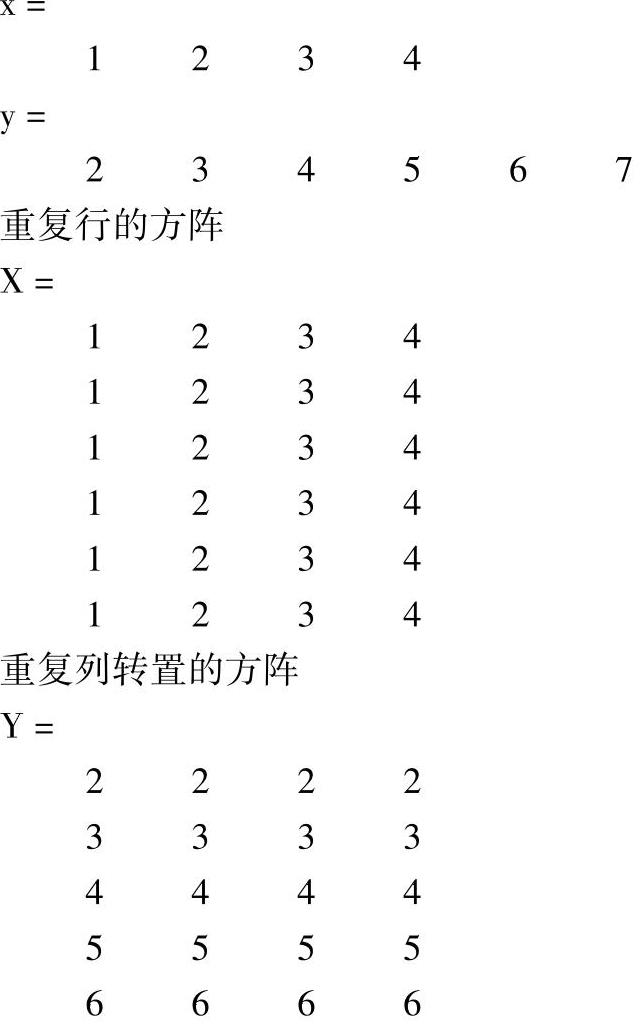
可见生成的平面网格点矩阵[X，Y]的行数等于列向量y的列数，列数等于行向量x的行数。

2）对平面网格点矩阵[X，Y]上的坐标（x，y）逐点计算函数值z=f（x，y），它的集合就是二维函数曲面的三维图形矩阵[x，y，z]。

如果输入参数列表中x是m维向量，y是n维向量，则z（x，y）是m×n阶二维矩阵。因此，二维曲面函数矩阵z的各点坐标是[x（i），y（j），z（i，j）]（i=1～m，j=1～n）。

2.三维曲面绘图函数

1）绘制三维网线图函数：

mesh( x,y,z)

其中，输入参数列表中x是n维向量，y是m维向量，z（x，y）是m×n阶二维矩阵。下面三维绘图函数中的输入参数（x，y，z）意义都与此相同。

绘制三维网格混合图形（包含等高线）函数：

meshc(x,y,z)

函数meshc的实质是创建一个与二维等高线图相匹配的网线图。

2）绘制三维曲面图函数：

surf( x,y,z)

该函数实质是对网线之间的网线元进行填充，形成三维曲面图。

绘制三维曲面混合图形（包含等高线）函数：

surfc( x,y,z)

该函数实质是创建一个与二维等高线图匹配的曲面图。(www.xing528.com)

3）等高线绘图函数。绘制二维等高线函数：

contour( z)

该函数实质是创建一个二维函数z（x，y）定义的二维等高线。

绘制三维等高线函数：

contour3( x,y,z,n)

其中，参数n是指定等高线条数。

4）标注等高线高程函数：

clabel(1

例5-8 绘制二维函数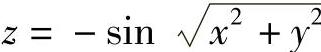的三维曲面图，其中二维变量x和y的取值范围都是[-4，4]。

%绘制旋转曲面

%产生二维网格矩阵

%[x，y]=meshgrid（-4：0.2：4）；

%二维函数表达式

M文件中的修饰参数说明：fontsize表示字号大小（常用12～16），fontname表示字体名称（如宋体、黑体、隶书等）。为了更加直观、清晰地显示图形的特征，可以单击图形窗口“Figure”工具栏中的“Rotate 3D”按钮，按住鼠标左键，移动鼠标对三维图形进行旋转操作。该M文件运行和旋转后显示的图形如图5-7所示。

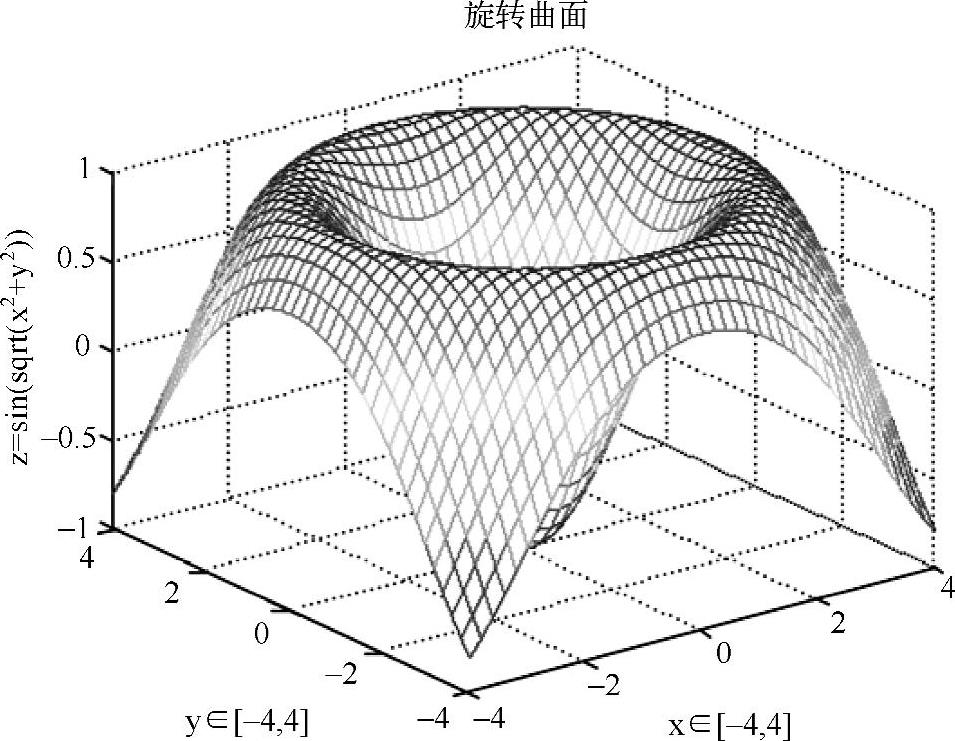
图5-7 三维旋转曲面图

5）绘制二维符号函数的三维图形。与一维符号函数绘图函数格式ezplot（fun，[xmin xmax]，m）类似，二维符号函数的绘图函数调用格式是：

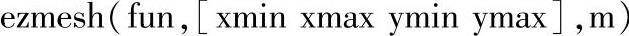
其中，fun表示M文件的函数名，或是二维变量为x，y的字符串；[xmin xmax ymin ymax]表示二维变量为x，y的函数绘图区间；m是描述图形性质的参数选项，见表5-1。

例5-9 绘制二维函数

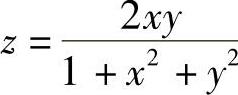的三维曲面图，其中二维变量x和y的取值范围分别是-5≤x≤5和-2π≤y≤2π。

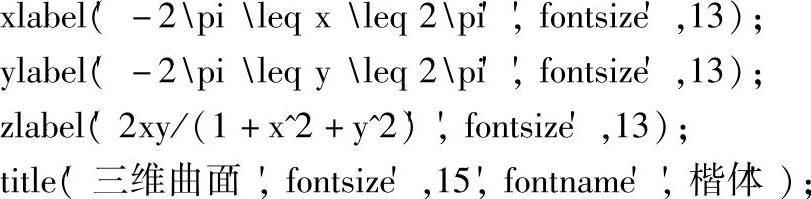
M文件的运算结果如图5-8所示。

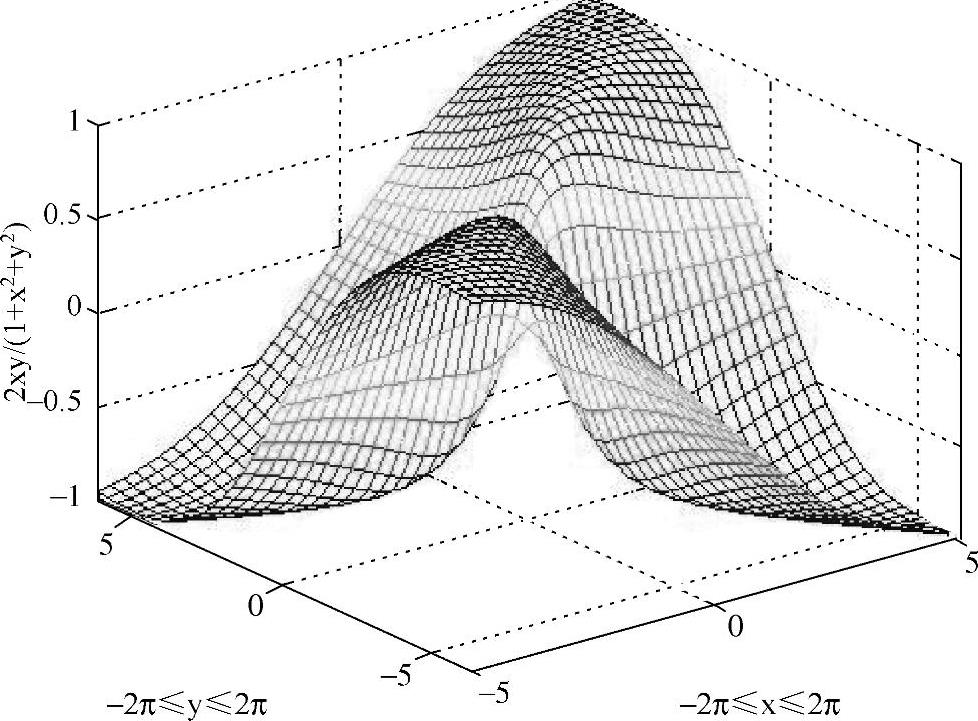
图5-8 绘制符号函数的三维曲面图