基带通用离散系统模型 - 一统江湖

上面几节的讨论我们都是直接用模拟信号来描述的，但在数字化时代，数字通信应用越来越广泛，模拟通信相对应用较少了。从数字通信系统来说，不管你怎么设计，采用什么调制方法，复用思想等，数据的解调都是以采样点为基础的，所以我们只要研究清楚采样点经过信道怎么变化就行了。那也就要求我们先建立基于采样点的离散系统传播模型，下面我们就看看相应的离散系统传播模型是什么样的。

先考虑相干时间里的信号传输模型，直接从基带信号入手说吧：

其中基带衰落α_i一般为复数。不妨设基带信号x_b（t）的（角频率）带宽为[-W，W]，则x_b（t）的采样表示为

代入式（13-20）有

以π/W为间隔对y_b（t）采样得到采样序列y[n]，那么

记发射信号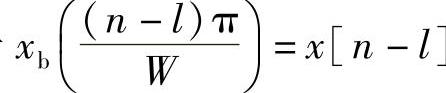，即第n-l个采样点的值，再记

那么，整个离散传播模型为

该离散传播模型如图13-11示意，其中“*”或“**”为系数的占位符，具体取值不影响讨论，暂不追究。

从式（13-25）所示的离散模型以及图13-11，我们可以看到，因为有多径传播，接收端的第n个采样点y[n]，除了包含有真正想要的x[n]的分量外，还包含比x[n]先发送的点的分量，这个也是码间串扰在离散模型下的体现。而对于所有路径，x[n-l]对y[n]贡献的分量为h[l]x[n-l]，其中h[l]是所有径合成而来的衰落系数，一般被称为信道抽头（Tap）或者信道的有效径。

实际上，只要发射端发的信号是

其中，g（t）可以是任意波形，比如sinc（t）、rect（t）、δ（t）等，接收端相应收到的N个值

y[0]，y[1]，…，y[N-1]

总是有

不过，对于相同的无线信道（每径延迟和衰落相同），对于固定的符号间隔T_s，按不同的信号波形g（t）发送x[n]，抽头h[l]除了有信道衰落本身的因素外，一般还和波形g（t）相关，如式（13-24）中的sinc项。又或者图13-12中b_i或b＇i对抽头的贡献，图13-12a中每个信道抽头h[l]由多径衰落系数α_i和波形相关的系数b_i确定，图13-12b类似。

图13-11 无线信道传播离散模型

图13-12 信道抽头与采样间隔

提醒

相同的无线信道（每径延迟和衰落相同）下，对于固定的符号间隔T_s，按不同的信号波形g（t）发送x[n]，相同的采样位置，信道抽头h[l]可能不同。

说到波形，从图13-12中还可以看到，如果接收端采样点有偏差（图中虚线发生偏移），其实也会改变b_i或b＇_i，进而会改变抽头。

提醒

相同的无线信道（每径延迟和衰落相同）下，对于固定的符号间隔T_s，按波形g（t）发送x[n]，采样位置偏移，信道抽头h[l]可能不同。

如果要把波形的影响去掉，我们可以考虑那些在符号时间内为常数的波形，比如Rect（t）、δ（t）等。

另一方面，对于相同的无线信道（每径延迟和衰落相同），除了波形对最后表现出来的信道抽头有影响外，符号时间间隔对信道抽头也有影响。比如图13-12中，按左边的以较小的符号间隔发送数据x[i]，接收端y[i]表达式里的每个抽头只由一条径确定，

h₀=α₁，h₁=α₂b₂，h₂=α₃b₃，h3=α₄b₄

而按右边的以较大的符号间隔发送数据x[i]，接收端y[i]表达式里的每个抽头一般由至少两条径确定，

h₀=α₁，h₁=α₂b₂＇+α₃b₃＇，…

通常我们说的符号时间间隔最后都是表现成采样间隔，也就是说采样间隔不同，最后呈现出来的信道抽头h_l就不同。

相同的无线信道（每径延迟和衰落相同）下，符号间隔长度不同或者说采样间隔不同，信道抽头h[l]可能不同。

同时，我们还可以看到，信道抽头h_l的值和抽头个数与信道的多径个数和每径衰落系数之间的关系。我们假想图13-12里的基本波形是方波Rect（t），即所有的b_i=b＇i=1来说明，如果采样间隔足够小（左图），那么此时每个抽头的值就分别和每条径的衰落系数相等，抽头个数也等于多径的条数；也就是说通过抽头能清楚地知道信道本身真实的多径个数和衰落情况，即对信道多径衰落的分辨率高。如果采样间隔比较大（右图），那么抽头个数会少于多径的条数，并且每个抽头的值是多条径衰落的叠加；此时通过抽头我们并不清楚信道本身真实的多径衰落情况，即对信道多径衰落的分辨率低；显然，采样间隔越大，对多径衰落的分辨率就越低。(www.xing528.com)

我们再看个例子，如图13-13里，假设发射端发射的序列x_i为

[x₀=1，x₁=0，x₂=0，…]

采用的波形为冲激信号δ（t），即发射的信号为

接收端收到的信号

其中，α_i表示延迟为τ_i的径的衰落系数。如果间隔T_s足够小，对应于图里虚线采样情形，那么接收端按T_s间隔对接收信号y（t）采样得到的采样点序列y[i]，满足

y[i]=h_ix₀=h_i其中，信道抽头h_i要么为0，要么等于某条径的衰落系数α_j，并且每条径的衰落系数α_j一定能对应到某个信道抽头h_i。当然对于信道抽头等于0的情况，我们也可以想象成对应于某条径，只不过该条径衰落得太狠了，衰落得一点儿都不剩了。很显然，采样间隔足够小的这种情况信道抽头真实地表达了信道多径衰落，即分辨率很高。如果间隔T_s太大，对应于图里实线采样情形，那么信道抽头h_i要么为0，要么等于某条径的衰落系数α_j，但是有很多径被漏掉了。很显然，采样间隔大的这种情况信道抽头不能真实地表达信道多径衰落，即分辨率低。

图13-13 信道冲激响应、信道抽头与采样间隔

在相干时间的假设下，虽然在一个信号持续的时间内，我们认为h_l是不变的，但在不同信号时间里，一般来说h_l是变化的，这个变化到底是按什么规律变化完全取决于周围环境。通常为了方便理论分析，并且实际环境也有很大可能存在的两个变化模型为瑞利衰落和莱斯衰落。

（1）瑞利衰落

如果假设当前无线信道有足够多的径，并且所有径独立分布，根据中心极限定理，那么所有径合成而来的衰落系数h_l将收敛于循环复随机变量（0，p²_l），即h_l的实部和虚部分别按照中心极限定理收敛到正态分布

。那么，该衰落的幅度h_l²的概率分布为瑞利（Ray-leigh）分布，瑞利分布也即为2阶的χ²（chi-square）分布。相应地，该信道称为瑞利衰落信道。

（2）莱斯衰落

和瑞利信道不一样，如果存在一条足够强的直射径（视距衰落），同时包含足够多独立的径，那么信道衰落可以建模成两部分

其幅度h_l²满足的概率分布称为莱斯（Rician）分布，这样的信道称为莱斯信道。可以看到，若k远小于1，那么第一个分量几乎为0，从而该衰落退化成瑞利分布；若k远大于1，那么第二个分量几乎为0，从而该衰落退化成确定不变的衰落。

暂时来看，通信的目的就是想办法从接收序列y[n]中得到序列x[n]，当然实际系统中还有噪声和可能的干扰，这个得到x[n]的估计值的过程一般也被称为均衡。显然，如果是没有码间串扰，即单抽头情形，均衡比较简单；如果有码间串扰，均衡看起来要复杂得多。具体的均衡方法和我们后续讲的其他模型的均衡也相关，这里暂时把问题提出来，解决方法就暂时不讲了，到时统一讲解。

上一节的讨论，我们是假设信号处于相干时间来讨论的。假设信道有L个抽头h_l（l=0，…，L-1）。那么，处于相干时间的信号，其对应的频率带宽上是什么样的情况？

我们前面讲DFT时，就讲过，采样点的DFT也能反映出采样点对应的真实模拟信号频谱上的情况，只是一个伸缩变化。下面我们就从离散系统看看是否能和相干带宽扯上关系。假设信道只有一个抽头，L=1，即

x[n]⇒y[n]=hx[n]

那么DFT变到频域来看为

DFT{x[n]}⇒hDFT{x[n]}

可以看到整个频带上的衰落都为h，即信号经历的衰落从频域来看是平衰落信道。注意，这并不表示相干带宽为无穷大，因为h本身其实可能是多条路径合成的，相干带宽还是有一个量，只是现在时延扩展远小于采样点间隔，即1/（2W），从而只体现成一条径。而相干带宽是时延扩展的倒数量级，信号带宽又是采样点间隔的倒数量级，所以此时相干带宽远大于信号x（t）带宽W而已。也就是说，信号既处于相干时间，信号带宽又远小于相干带宽时，信号传播模型最简单。下面考虑哪些情况下，这两个条件容易同时满足呢？

三言两语

信号既处于相干时间，信号带宽又远小于相干带宽时，信号传播模型最简单。

如果时延扩展和一个采样点间隔可比拟，甚至超过一个采样点间隔，那么必存在多个抽头，则传播模型为

那么DFT变到频域来看为

一般来说，右边的接收信号不可能刚好也存在某个h，使得右边接收信号可以写成

hDFT{x[n]}

然而，应该可以写成

这里，DFT{x[n]}_i表示序列x[n]的DFT的第i个分量。其中，至少有两个h^_i和h^_j相差比较大，也就使得整个频带不再处于同一个相干带宽中了，即信号经历的衰落从频域来看是频选衰落信道。也就是说，若在时域有码间串扰（抽头多于1个），那么信号带宽必然大于相干带宽；反之，若信号带宽大于相干带宽，那么信号必存在码间串扰。

话说h^_i有什么规律可循吗？比如和h_i是什么关系？或者有什么办法把h^_i变得有规律可循？这些问题稍后再讲。