1.多径传播
现实环境中,发射源和接收机之间有很多物体,包括建筑、汽车、树木等,这些物体都会造成电磁波的反射、散射,因此发射源的电磁波会通过多条路径到达接收端。从而对某点来说,最后呈现出来的振动是多条路径触发的振动的合成,但是每一条路径触发的振动的功率可能不相同,并且振动开始时间也可能不相同,然而每一个都形如
αix(t-τi)那么,对于某点来说,整体呈现出来的振动为

其中,和式表示所有路径触发振动的叠加。如果接收机静止,接收机也将接收到这样一个信号。
接下来,多径其实可以分为两种情况:客观存在的多径和具有时间分辨度的多径。对于客观存在的多径,有可能所有多径的延迟完全一样,但确实是多径,只是从时间上表现出来像一条径一样。比如,发射端发了信号x(t),有多条路径同时到达接收端,则接收信号为
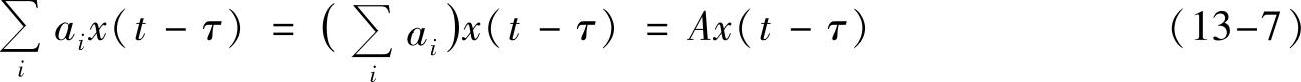
即本来是多径传播,最后呈现出来的效果和一条径传播的效果一样。
具有时间分辨度意义上的多径,则是指一定包含延迟不同的路径,接收信号为

其中,各径延迟τi两两不等。当然,这里的一个时延分量仍然可能实际上是由多条延迟相同的路径叠加出来的,接下来我们暂时仅考虑具有时间分辨意义上的多径。
当环境发生变化,甚至天气发生变化,或者发生相对运动时,如上面讨论的一样,每条路径接收到的功率和相位都是随时间发生变化的,甚至路径的个数也是发生变化的。当然我们总是可以假设有无穷多条路径,只是有时候某些路径的功率变为0而已。那么也就是说,一般情况下,对于多径情形,接收到的信号形如
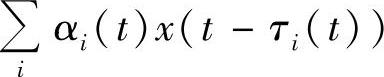
2.相干带宽
在讲相干带宽之前,我们必须先了解信道的频率选择性,频率选择性主要是由无线信道的多径传播特性引起的。频率选择性是说,对不同频点,在无线信道中的衰落情况不一样,有些频点能量衰减小,有些频点能量衰减大。如果只是先体会频率选择性,最简单的情况是看静止情形下时延不一样的多径信道,那我们就先看看吧。
对绝对静止多径信道情形,假设发射端发射的是信号x(t),其频谱为X(ω)。接收端接收到的时域信号为
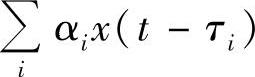
看看接收信号的频谱,不同时延对应到频域就是相位旋转,
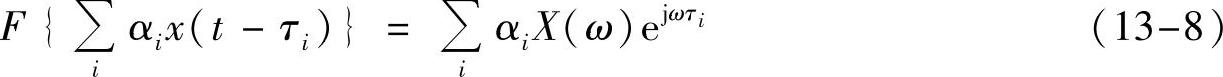
我们看相对于发射端信号的频谱X(ω),对于频点ω的衰落系数为(https://www.xing528.com)
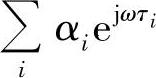
若频点ω变化,一般对应的衰落系数跟着变化。可以看到,各径的相位旋转对于不同频点形成不同夹角,再叠加后的整体效果可能相涨或者相消。如果在某一个频带内整体效果近似相等,例如都是相涨或者相消,称该频带处于相干带宽内。
更具体地,直观上就可以想象得到,当两个频点ω1和ω2隔得很近时,它们对应的衰落系数相关性强,即存在△ω',使得差值

很小。也即两个频点分别对应的衰落系数的模近似相等,只有一个相位差ej△ω',或者说只有一个夹角△ω'。为了简单,下面我们仅以两径为例来做更深入的讨论。假设接收信号频谱为

其中,τ2>τ1>0。对于两个频点ω2>ω1,ω2对应的两个衰落系数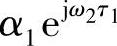 和
和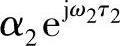 分别是ω1对应的两个衰落系数
分别是ω1对应的两个衰落系数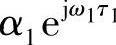 和
和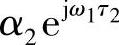 的旋转,旋转角度分别是τ1(ω2-ω1)和τ2(ω2-ω1),角度差为(ω2-ω1)(τ2-τ1)。因为信道延迟不随频点变化,从而角度差仅由两个频点的间隔确定。显然,当两个旋转角度差很小时,即ω2-ω1很小时,两个频点总的衰落系数近似也只有一个角度旋转的差别(相位差别);而当旋转角度差越来越大时,两个频点总的衰落系数之间的关系越来越没有规律,不论幅度还是相位都是如此。如图13-6所示,图中的ti对应于这里说的τi。
的旋转,旋转角度分别是τ1(ω2-ω1)和τ2(ω2-ω1),角度差为(ω2-ω1)(τ2-τ1)。因为信道延迟不随频点变化,从而角度差仅由两个频点的间隔确定。显然,当两个旋转角度差很小时,即ω2-ω1很小时,两个频点总的衰落系数近似也只有一个角度旋转的差别(相位差别);而当旋转角度差越来越大时,两个频点总的衰落系数之间的关系越来越没有规律,不论幅度还是相位都是如此。如图13-6所示,图中的ti对应于这里说的τi。

图13-6 不同旋转角度差别
我们想知道,不同径的角度差别在哪个范围内,即两个频点的差在哪个范围内,能近似保持总的衰落系数仅有相位差别呢?从数学知识,可以了解到,当这个角度差别小于π/4,甚至更严格点,要求小于π/16时(还可以更严格),可以近似保持这种规律。即要求

也就是说,任何宽度为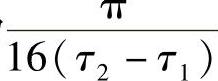 的一段带宽上的频点都处于相干带宽内。将两径推广到多径类似,不论怎样,相干带宽的量级大概为时延扩展的倒数。
的一段带宽上的频点都处于相干带宽内。将两径推广到多径类似,不论怎样,相干带宽的量级大概为时延扩展的倒数。
性质13-1 无线信道相干带宽的量级为该信道时延扩展的倒数的量级。比如,LTE里采用的经典城区(TU)信道模型里,时延扩展大概有几微秒(μs),以1 μs计算,相干带宽量级为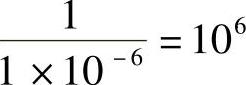 Hz,即1000 kHz,加上一些系数调整,相干带宽大概为几百kHz的样子。
Hz,即1000 kHz,加上一些系数调整,相干带宽大概为几百kHz的样子。
3.相干带宽无传递性
注意,相干带宽是近似相等的一段频率宽度,只要满足这个宽度就是相干带宽,没有位置的概念。特别重要的是,相干带宽没有传递性。即不能说频率区间[ω0,ω0+△ω]处于相干带宽,而频率区间[ω0+△ω1,ω0+△ω2]也处于相干带宽,其中
ω0<ω0+△ω1<ω0+△ω<ω0+△ω2那么就得出[ω0,ω0+△ω2]也处于相干带宽。这是不对的,没有这样的逻辑,即没有传递性。

图13-7 相干带宽无传递性
最后,如果信号带宽小于信道相干带宽,从频域来看,称信号经历的衰落为平衰落;如果信号带宽大于相干带宽,从频域来看,称信号经历的衰落为频率选择性衰落。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




