分组码及其应用：理解与应用实践

分组码这里我们只介绍线性分组码，如字面意思，线性分组码表示这种码既是线性码，又是分组码。这类码通常可以由一个生成矩阵来表征。比如，把k个原始信息比特生成长度为n的码字比特的线性分组码对应一个n×k的矩阵G，即

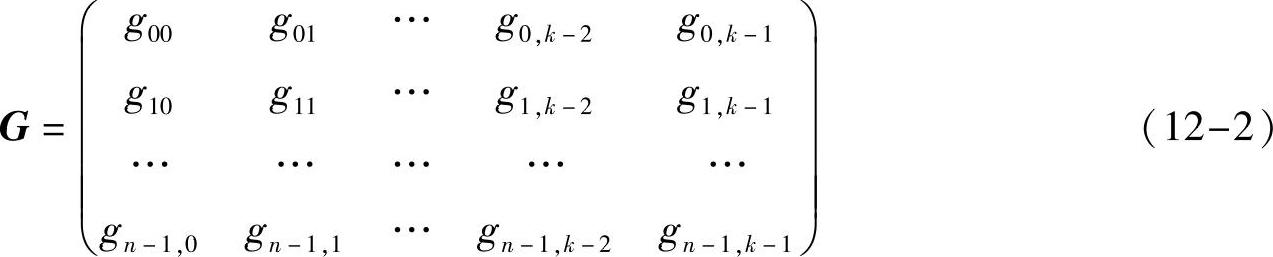
假设原始信息比特为x=[x₀，x₁，…，x_k-1]^T，那么码字比特

C=[C₀，C₁，…，C_n-1]^T=Gx（12-3）其中

特别地，如果生成矩阵G形如

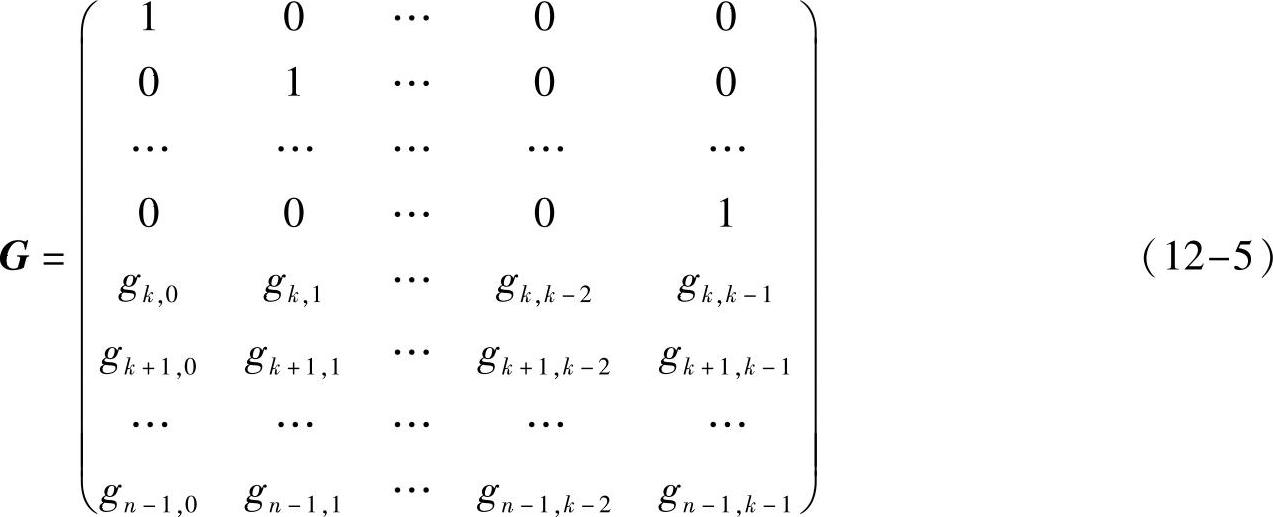
即前k行k列是单位矩阵I_k×k，那么生成的编码则为系统码，因为码字比特C里，前k个比特分别就是原始信息比特x。当然，形式上其实并不要求式（12-5）里前k行一定连续出现，只要生成矩阵G里包含这k行就是系统码。不失一般性的讨论，我们都假设是连续的这种情况。

若线性分组码是系统码，那么其生成矩阵可以写成

对于任何给定的原始信息比特x，其对应码字C的前k个比特就是x，这前k个比特称为信息位。那么，对于不同原始信息比特，只需要确定剩下的n-k个比特，这n-k个比特称为校验位（或监督位）。基于这个分析，也可直接把G＇称为生成矩阵，则校验位为

[C_k，…，C_n-1]^T=G＇x=G＇[C₀，…，C_k-1]^T（12-7）(www.xing528.com)

上式也可变换成

G＇[C₀，…，C_k-1]^T-I（n_-k）×（n_-k）[Ck，…，Cn_-1]^T=0（12^-8）

即

[G＇（n_-k）×k^I（n-k）×（n-k）][C0，…，Ck-1，Ck，…，Cn-1]^T=0（12^-9）

也就是说，如果一串比特序列是对应于系统码G＇的码字，那么看是否满足式（12-9）就可以了。鉴于此，称矩阵[G＇（n_-k）×k^I（n_-k）×（n-k）]为校验矩阵。

具体的线性分组码有很多，比如汉明码、Golay码、Reed-Muller码和LDPC码等，不同的线性分组码对应不同的生成矩阵。线性分组码通常用于编码少量的原始信息比特，主要是因为大多数线性分组码对应的编码生成矩阵都不会很大。因为线性分组码在应用时，显然需要存储生成矩阵，如果矩阵太大，且生成矩阵没有特殊结构，生成矩阵的存储都是问题，比较麻烦的事情。例如，LTE中用Reed-Muller码（32，O）和（20，A）来编码HARQ-ACK、CQI等控制信息，这些信息一般只有几个比特；同样TD-SCDMA中用Reed-Muller码（48，10）来编码控制信息。LTE中（20，A）生成矩阵如表12-1所示，能把A≤13个原始信息比特[x₀，…，x_A-1]编码成长度20的码字[C₀，…，C₁₉]，其中

表12-1 LTE里Reed-Muller码（20，A）生成矩阵

当然，也有部分生成矩阵具有特殊结构的线性分组码，可以稍微能编码相对比较长的原始信息比特。比如LDPC，如其名，低密度校验码（Low Density Parity Code，LDPC）表示生成矩阵是矩阵里1很少的稀疏矩阵，其存储相对容易。例如，IEEE 802.11n里就采用LDPC对数据进行编码，每次能编码上千个原始信息比特。